X
Код презентации скопируйте его
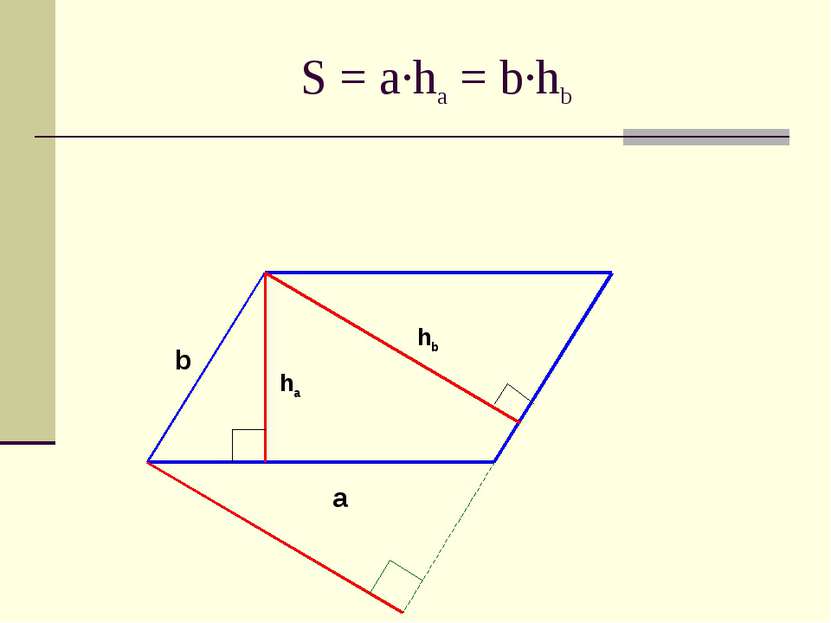
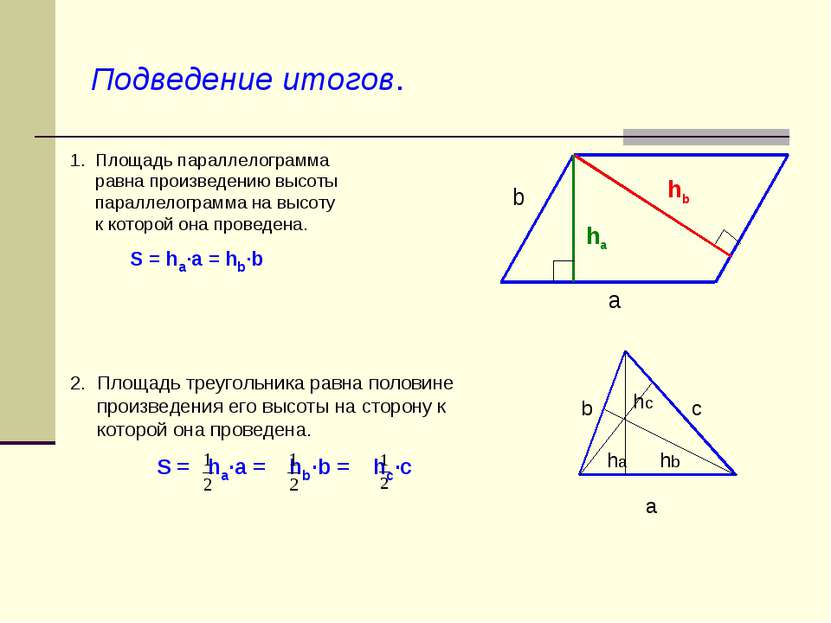
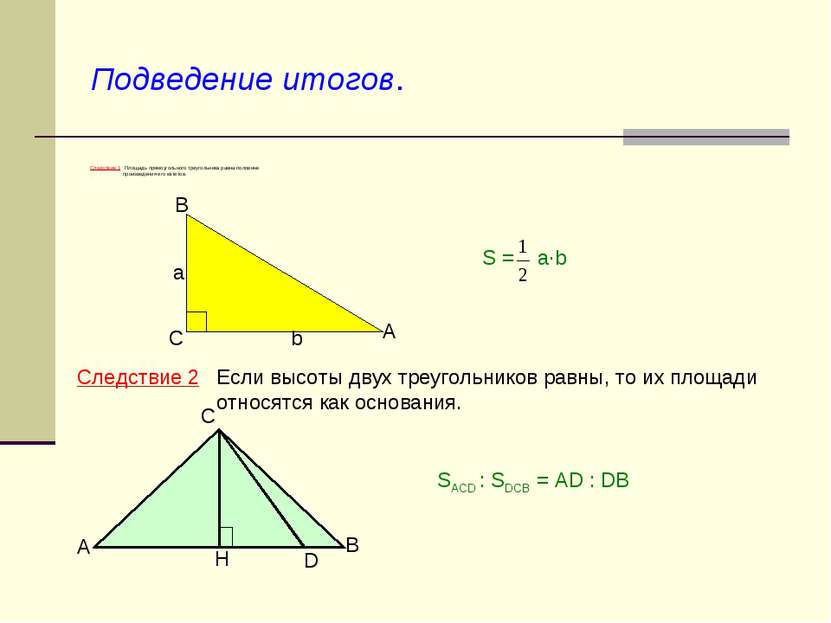
Площадь параллелограмма и треугольника
Скачать эту презентацию
Презентация на тему Площадь параллелограмма и треугольника
Скачать эту презентациюCлайд 1
Тема: Площадь параллелограмма и треугольника. Цель. Вывести формулы для вычисления площади параллелограмма и треугольника. Решать задачи на применение формул площади фигур; свойств площади.
Cлайд 2
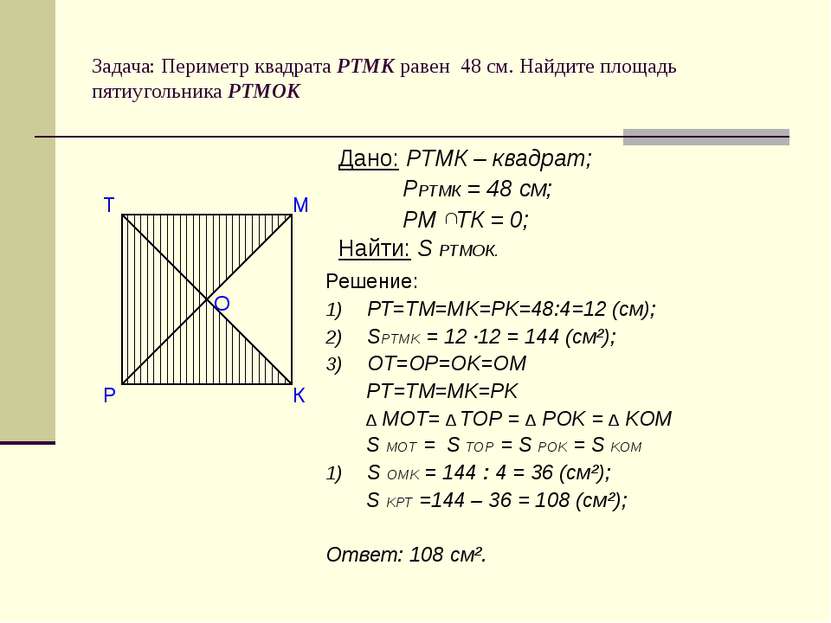
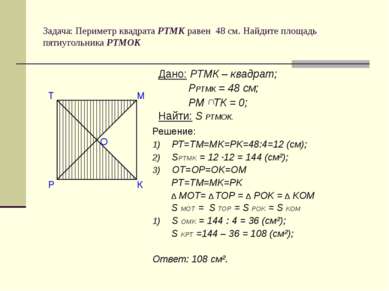Задача: Периметр квадрата РТМК равен 48 см. Найдите площадь пятиугольника РТМОК Решение: РТ=ТМ=МK=РK=48:4=12 (см); SPTMK = 12 ·12 = 144 (cм²); OT=OP=OK=OM PT=TM=MK=PK ∆ MOT= ∆ TOP = ∆ POK = ∆ KOM S MOT = S TOP = S POK = S KOM S OMK = 144 : 4 = 36 (cм²); S KPT =144 – 36 = 108 (cм²); Ответ: 108 cм². Дано: РТМК – квадрат; РРТМК = 48 см; РМ ТК = 0; Найти: S РТМОК. О М К Р Т
Cлайд 3
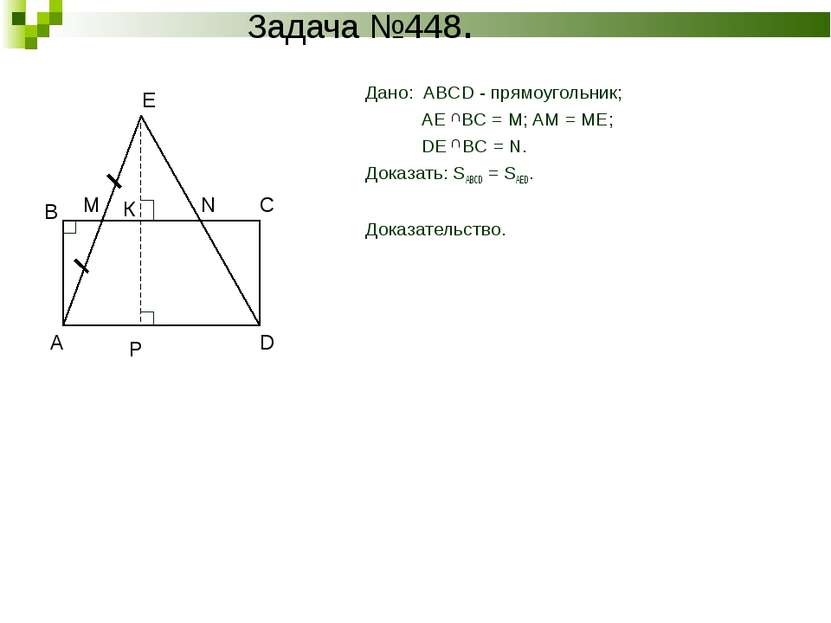
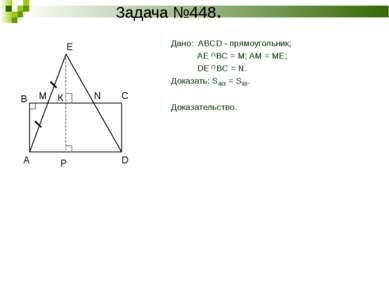Задача №448. Дано: ABCD - прямоугольник; AE BC = M; AM = ME; DE BC = N. Доказать: SABCD = SAED. Доказательство. К
Cлайд 4
Любые два равновеликих многоугольника равносоставленны. Теорема Бойяи – Гервина. Ф.Бойяи – венгерский математик, доказал это утверждение в 1832 г. П.Гервин – немецкий математик–любитель, независимо от Ф.Бойяи доказал её в 1833 году. Следствие: любой многоугольник можно разрезать на такие части, из которых можно составить равновеликий этому многоугольнику квадрат. Доказательство теоремы в литературе: В.Ф.Каган «О преобразовании многогранников» В.Г.Болтянский «Равновеликие и равносоставленные фигуры».
Cлайд 5
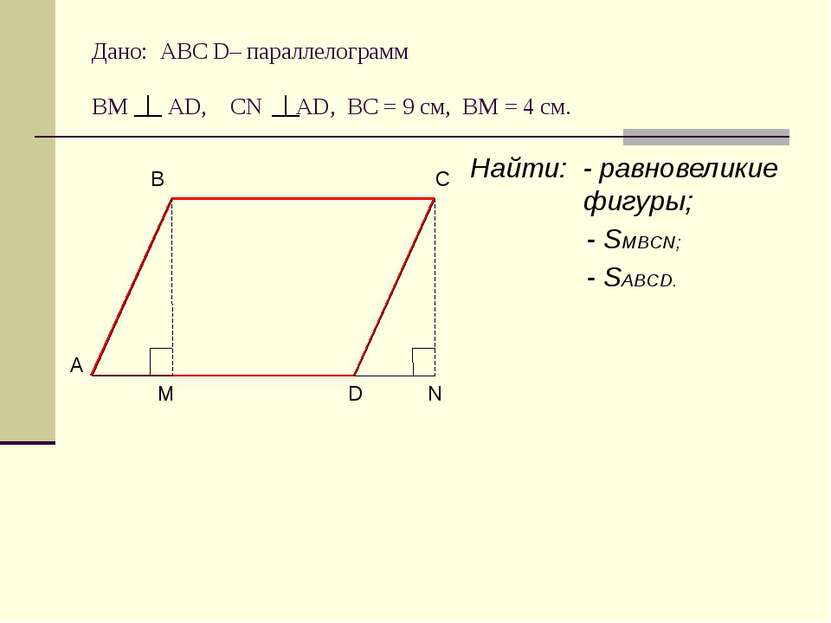
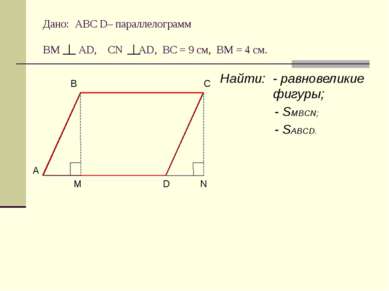Дано: АВС D– параллелограмм ВМ АD, CN AD, BC = 9 cм, ВМ = 4 см. Найти: - равновеликие фигуры; - SMBCN; - SABCD.
Cлайд 6
Тема: Площадь параллелограмма и треугольника.
Cлайд 7
А D С В Сколько высот можно провести в параллелограмме?
Cлайд 8
S = a·ha = b·hb
Cлайд 9
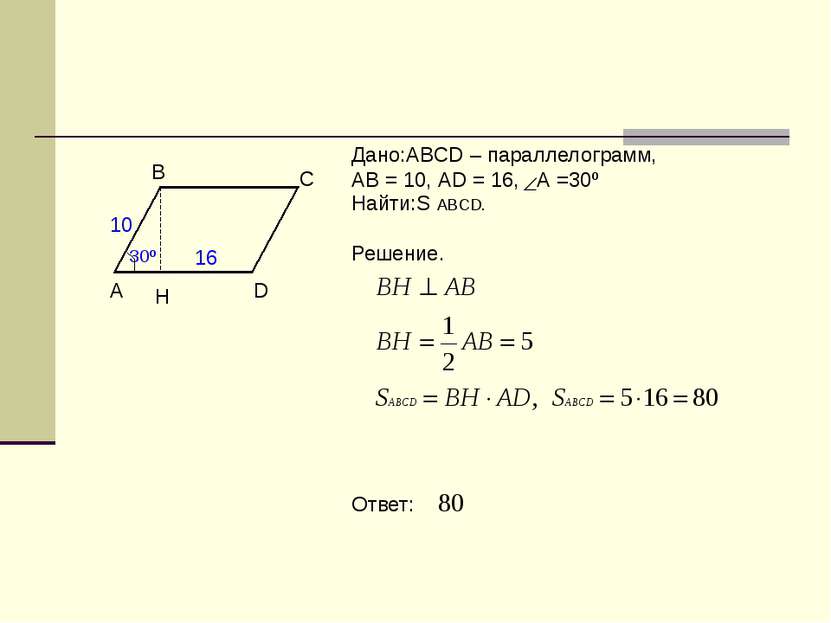
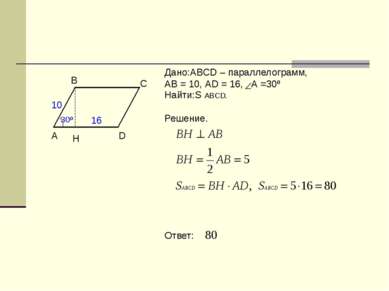Дано:ABCD – параллелограмм, АВ = 10, АD = 16, А =30º Найти:S ABCD. Решение. Ответ: 30º A В С D H 16 10
Cлайд 10
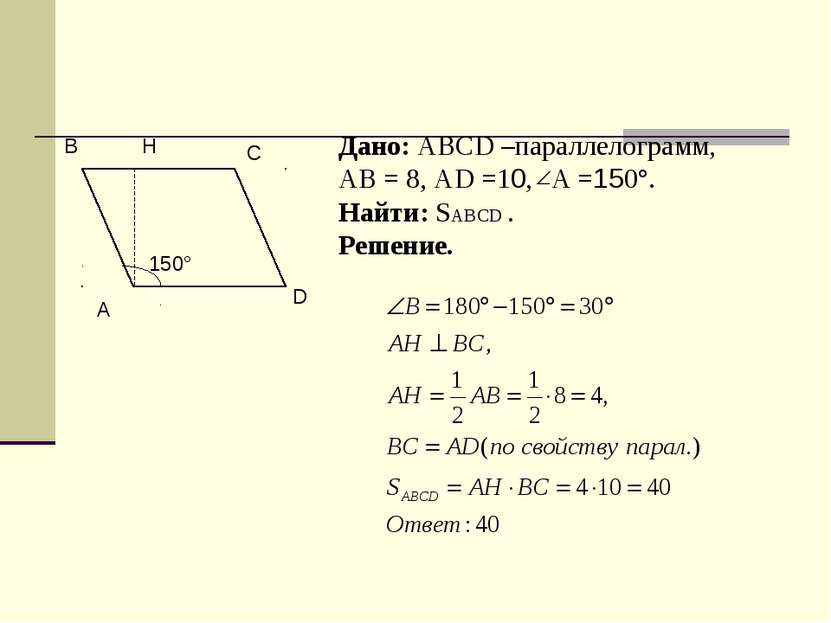
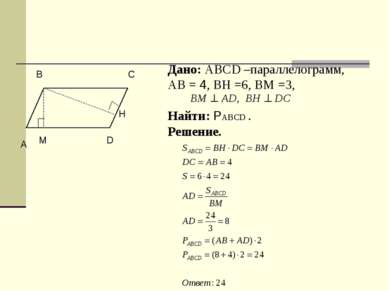
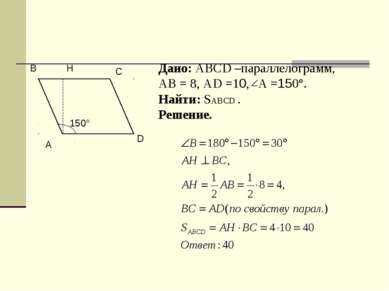Дано: ABCD –параллелограмм, АВ = 8, АD =10, A =150°. Найти: SABCD . Решение. А B D C H 150°
Cлайд 11
Дано: ABCD –параллелограмм, АВ = 4, ВН =6, ВМ =3, Найти: РABCD . Решение. C
Cлайд 12
Домашнее задание: Вопросы для повторения к главе VI 4 – 5; № 459(б), № 469. Вывести формулу площади дельтоида.
Cлайд 13
Подведение итогов. 2. Площадь треугольника равна половине произведения его высоты на сторону к которой она проведена. S = ha·a = hb·b = hс·с 1. Площадь параллелограмма равна произведению высоты параллелограмма на высоту к которой она проведена. S = ha·a = hb·b
Cлайд 14
Подведение итогов. Следствие 1 Площадь прямоугольного треугольника равна половине произведения его катетов. Следствие 2 Если высоты двух треугольников равны, то их площади относятся как основания. С В А а b S = a·b A B C D H SACD : SDCB = AD : DB
