X
Код презентации скопируйте его
Геометрия.Введение. Аксиоматика.
Скачать эту презентацию
Презентация на тему Геометрия.Введение. Аксиоматика.
Скачать эту презентациюCлайд 1
ГЕОМЕТРИЯ Гео – земля Метрео – измеряю (греч.) Волконская Н.Н . ГБОУ школа № 644 Санкт-Петербург
Cлайд 2
Египет 2000 г до н.э. Геродот V век до н.э.
Cлайд 3
IV – V вв. до н.э. – ПИФАГОРЕЙСКАЯ ШКОЛА ПЕНТОГРАММА
Cлайд 4
М е ф и с т о ф е л ь: Нет, трудновато выйти мне теперь Тут кое-что мешает мне немного: Волшебный знак у вашего порога. Ф а у с т: Не пентаграмма ль этому виной? Но как же, бес, пробрался ты за мной? Каким путем впросак попался? М е ф и с т о ф е л ь: Изволили ее вы плохо начертить, И промежуток в уголку остался, Там, у дверей, – и я свободно мог вскочить. Ф а у с т. Г е т е.
Cлайд 5
Египетский
Cлайд 6
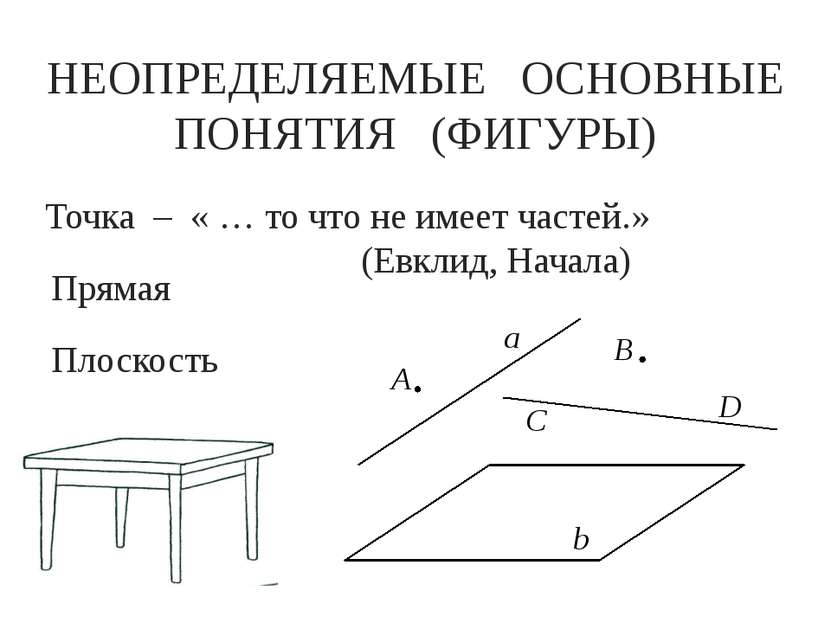
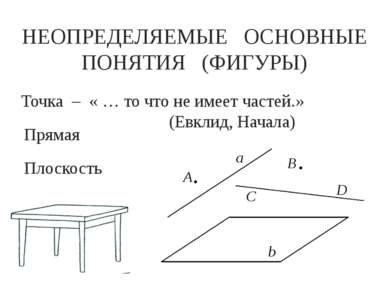НЕОПРЕДЕЛЯЕМЫЕ ОСНОВНЫЕ ПОНЯТИЯ (ФИГУРЫ) Точка – « … то что не имеет частей.» (Евклид, Начала) Прямая Плоскость а А В D С b
Cлайд 7
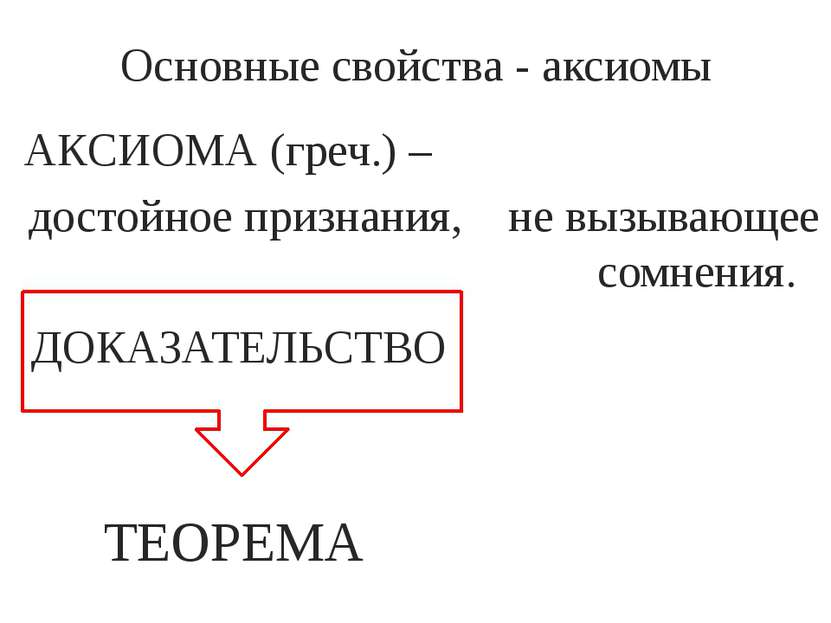
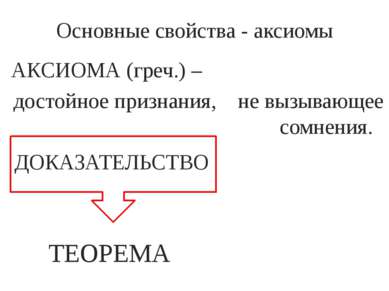АКСИОМА (греч.) – достойное признания, не вызывающее сомнения. Основные свойства - аксиомы ДОКАЗАТЕЛЬСТВО ТЕОРЕМА
Cлайд 8
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ А B C D а
Cлайд 9
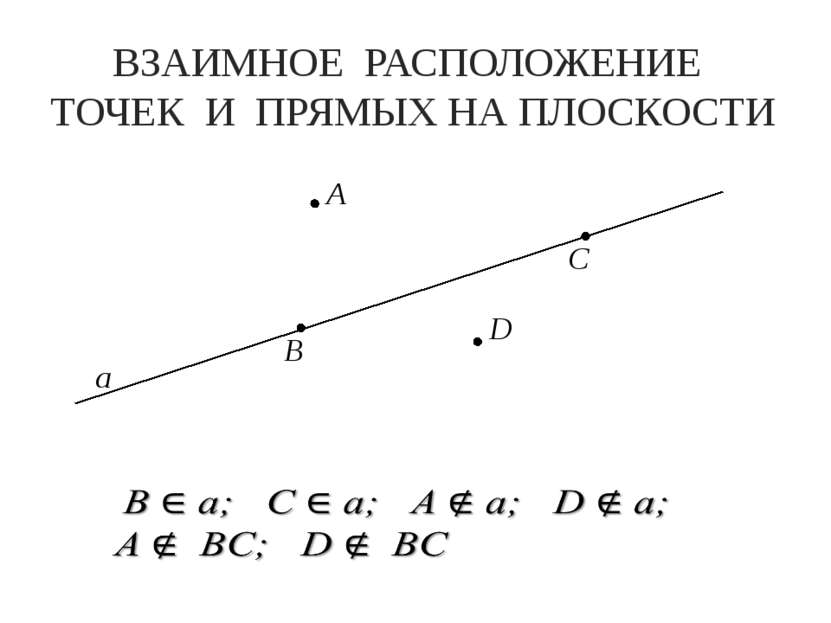
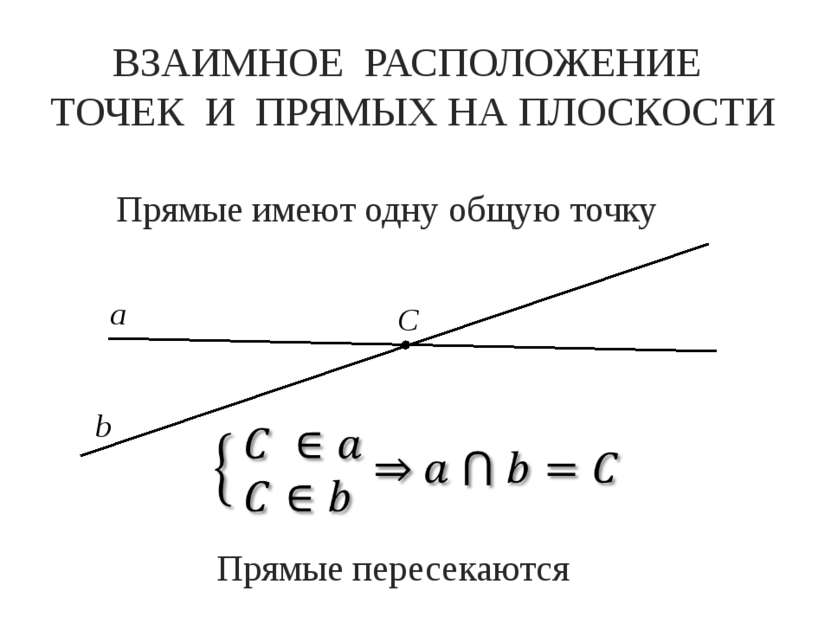
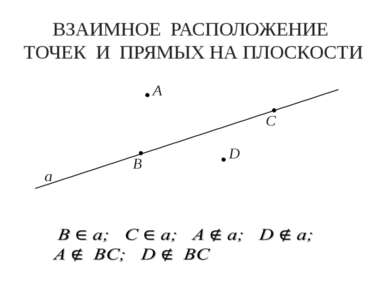
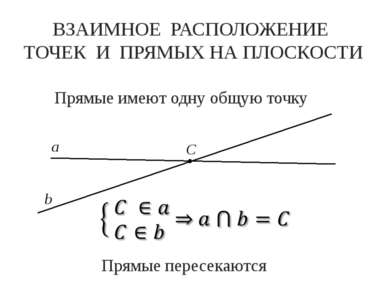ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ а b C Прямые пересекаются Прямые имеют одну общую точку
Cлайд 10
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ с d Прямые не имеют общих точек Прямые параллельны А1. Параллельные прямые не пересекаются
Cлайд 11
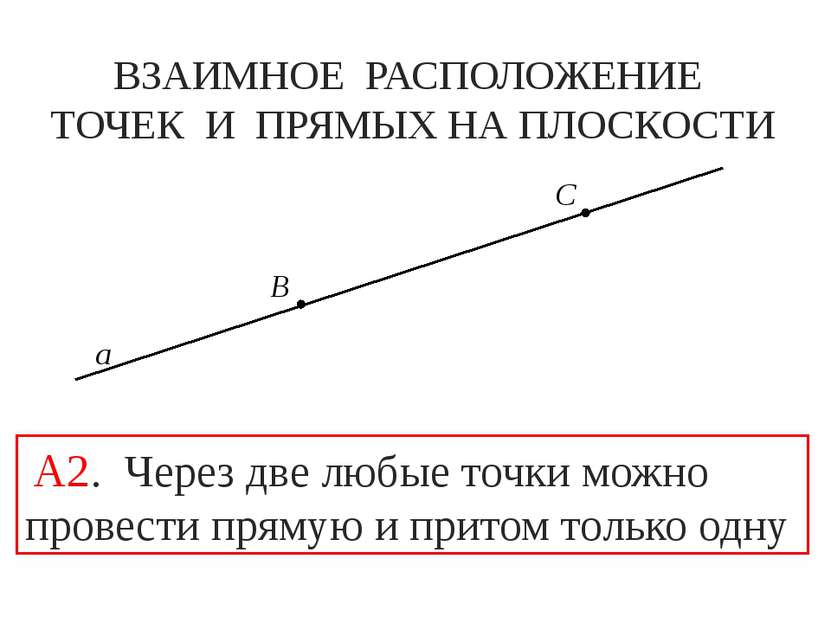
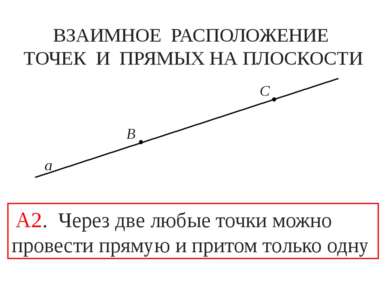ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ B C а А2. Через две любые точки можно провести прямую и притом только одну
Cлайд 12
Провести четыре прямые так чтобы каждые две из них пересекались, но никакие три не пересекались в одной точке. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
Cлайд 13
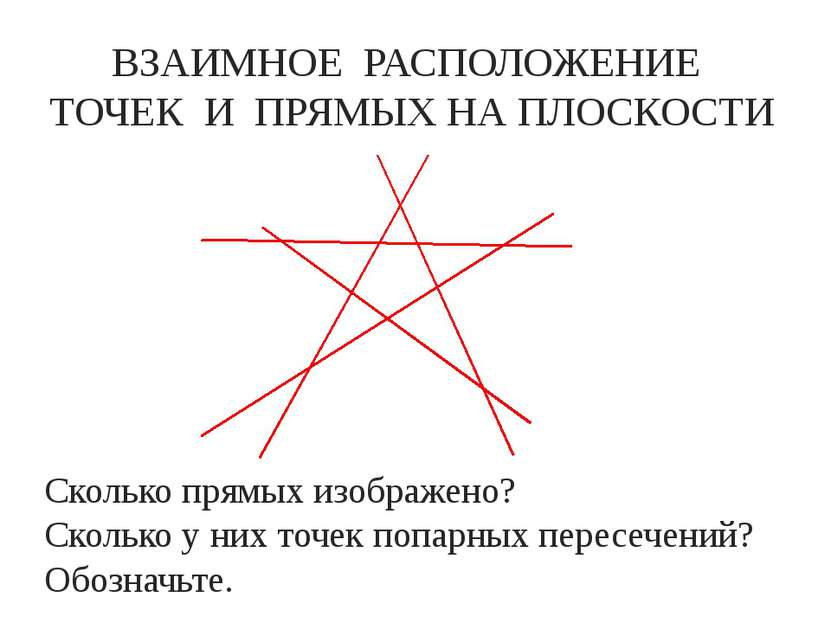
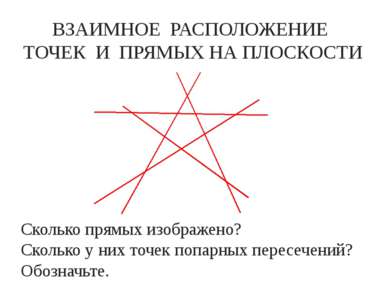ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ Сколько прямых изображено? Сколько у них точек попарных пересечений? Обозначьте.
Cлайд 14
Сколько прямых можно провести через а) три точки б) четыре точки Рассмотрите все возможные случаи. Выполните построения. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ
Cлайд 15
Домашнее задание СПАСИБО ЗА РАБОТУ !
