X
Код презентации скопируйте его
Четыре замечательные точки треугольника
Скачать эту презентацию
Презентация на тему Четыре замечательные точки треугольника
Скачать эту презентациюCлайд 1
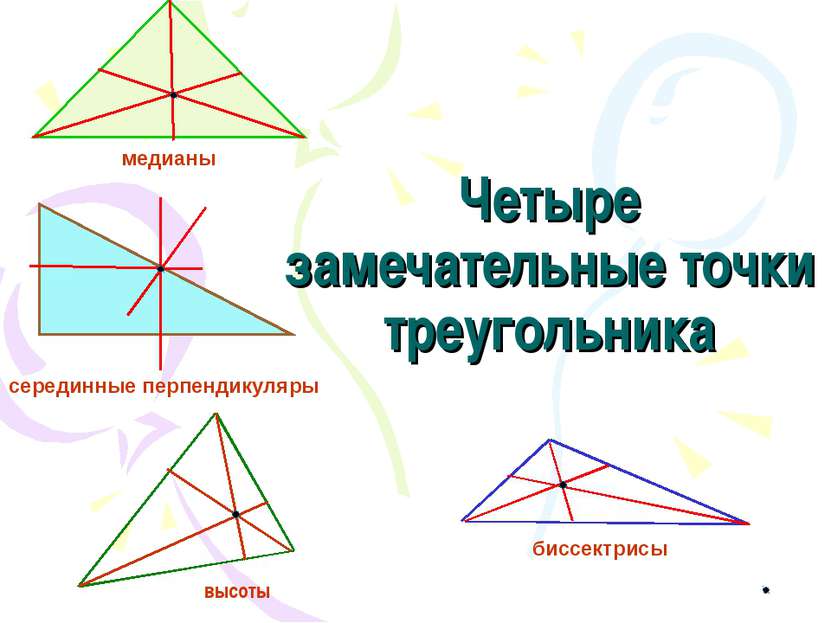
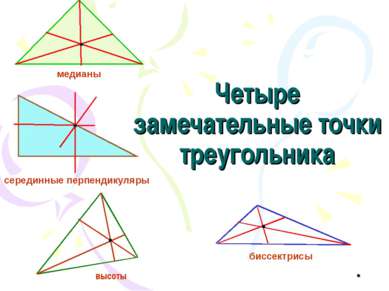Четыре замечательные точки треугольника высоты биссектрисы серединные перпендикуляры медианы
Cлайд 2
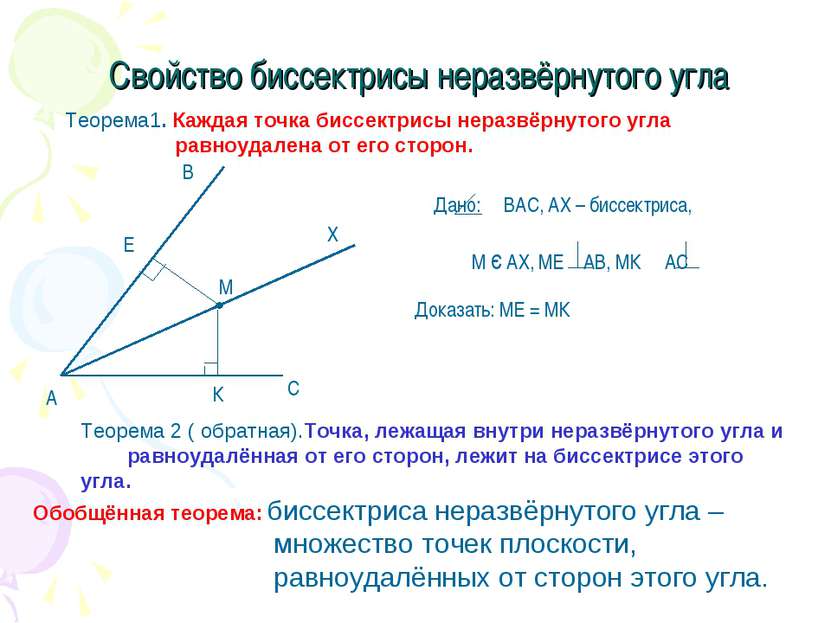
Свойство биссектрисы неразвёрнутого угла Теорема1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Доказать: МЕ = МК Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла. Обобщённая теорема: биссектриса неразвёрнутого угла – множество точек плоскости, равноудалённых от сторон этого угла.
Cлайд 3
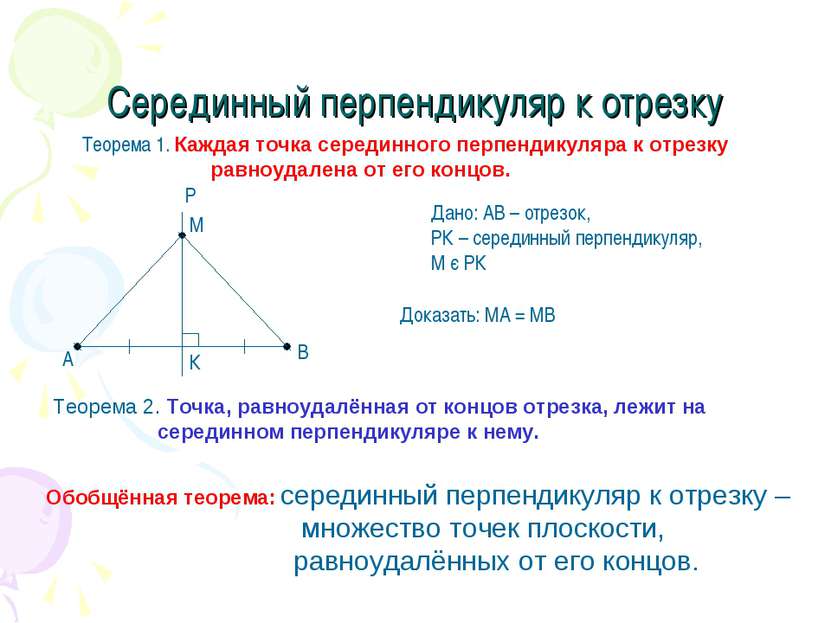
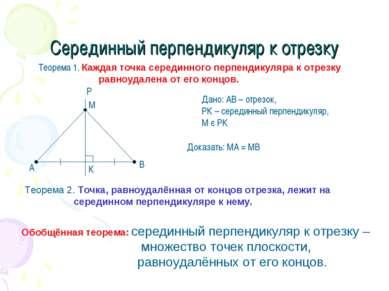Серединный перпендикуляр к отрезку Теорема 1. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. Дано: АВ – отрезок, РК – серединный перпендикуляр, М є РК Доказать: МА = МВ Теорема 2. Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. Обобщённая теорема: серединный перпендикуляр к отрезку – множество точек плоскости, равноудалённых от его концов.
Cлайд 4
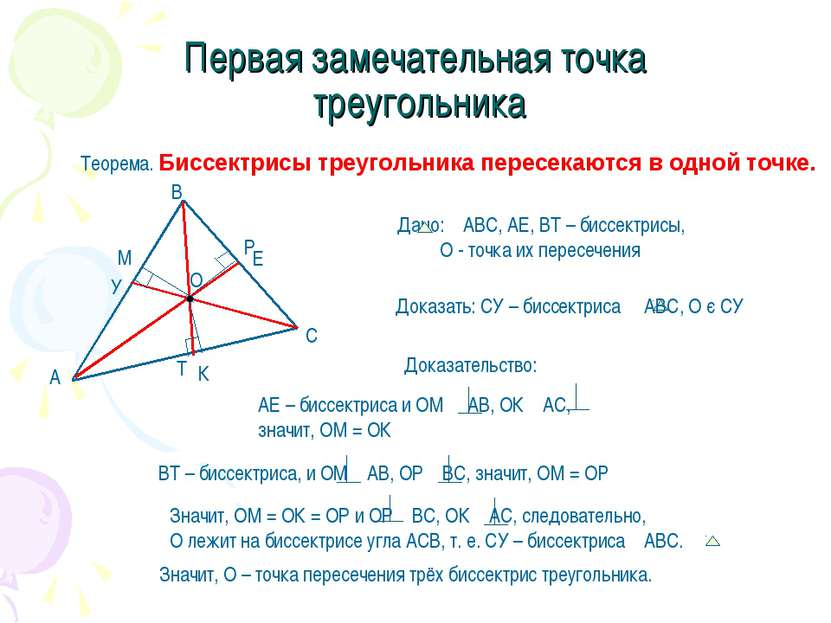
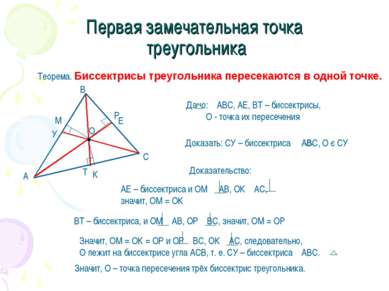Первая замечательная точка треугольника Теорема. Биссектрисы треугольника пересекаются в одной точке. Доказательство: Значит, О – точка пересечения трёх биссектрис треугольника.
Cлайд 5
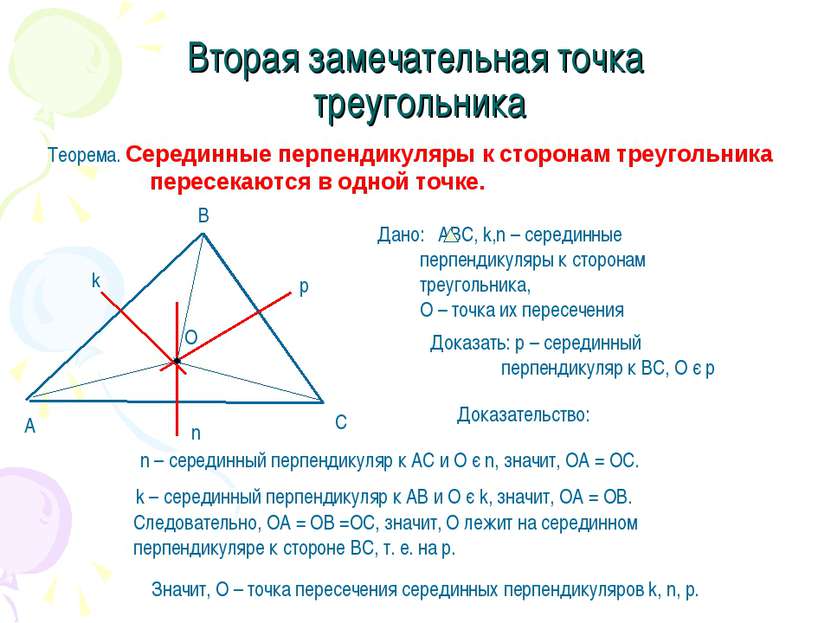
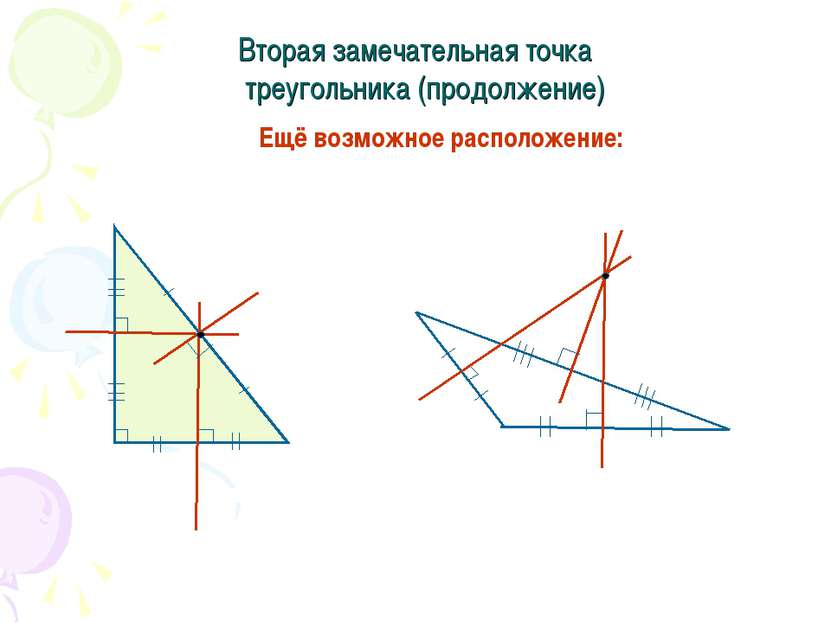
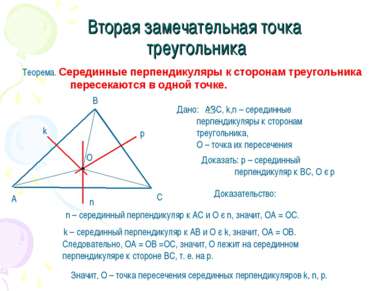Вторая замечательная точка треугольника Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказать: р – серединный перпендикуляр к ВС, О є р Доказательство: n – серединный перпендикуляр к АС и О є n, значит, ОА = ОС. k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ. Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном перпендикуляре к стороне ВС, т. е. на р. Значит, О – точка пересечения серединных перпендикуляров k, n, p.
Cлайд 6
Вторая замечательная точка треугольника (продолжение) Ещё возможное расположение:
Cлайд 7
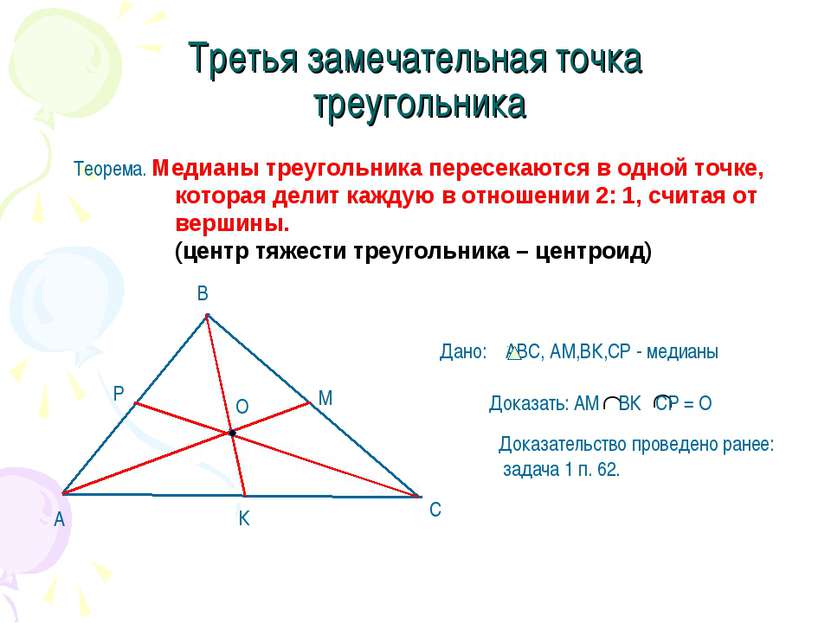
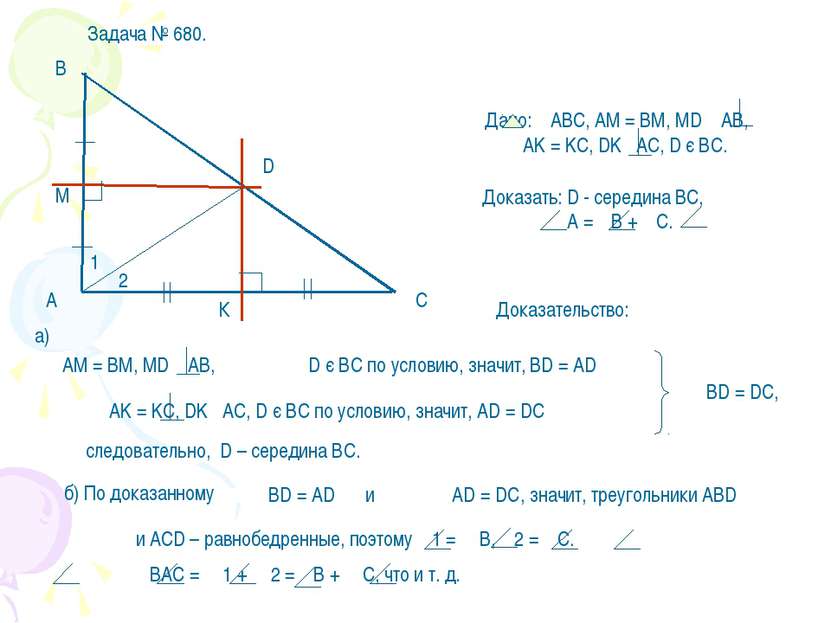
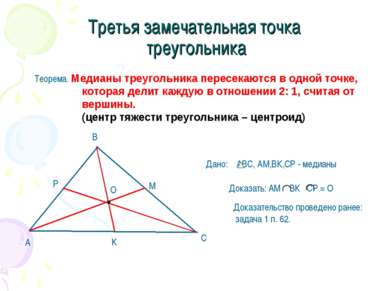Третья замечательная точка треугольника Теорема. Медианы треугольника пересекаются в одной точке, которая делит каждую в отношении 2: 1, считая от вершины. (центр тяжести треугольника – центроид) Доказательство проведено ранее: задача 1 п. 62.
Cлайд 8
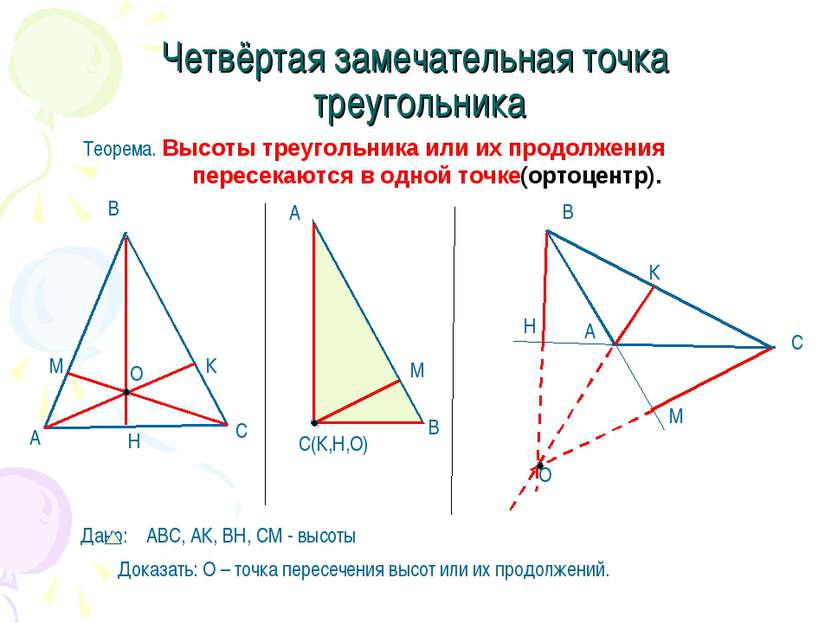
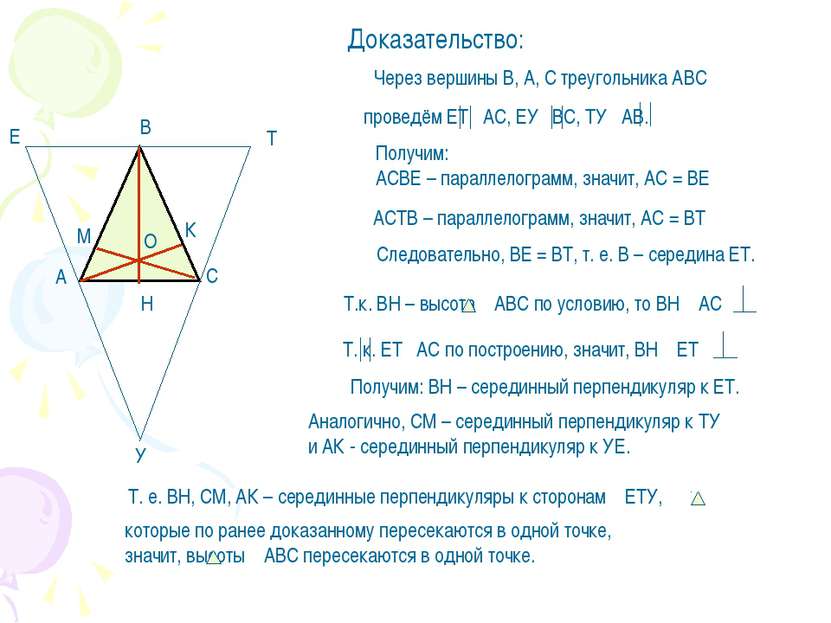
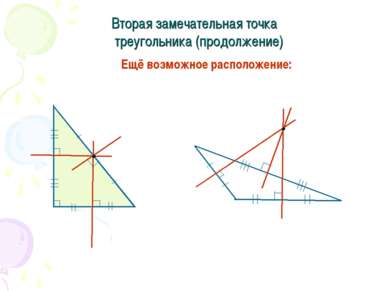
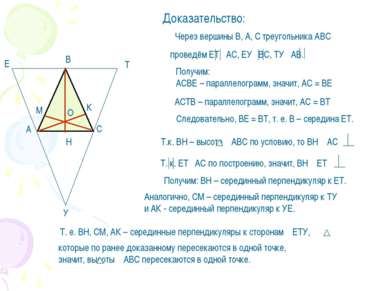
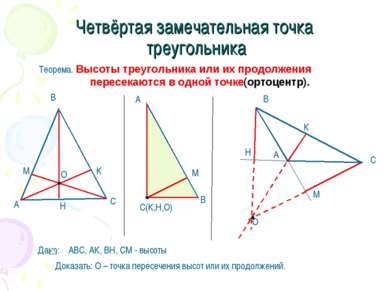Четвёртая замечательная точка треугольника Теорема. Высоты треугольника или их продолжения пересекаются в одной точке(ортоцентр).
Cлайд 9
Доказательство: Получим: АСВЕ – параллелограмм, значит, АС = ВЕ АСТВ – параллелограмм, значит, АС = ВТ Следовательно, ВЕ = ВТ, т. е. В – середина ЕТ. Получим: ВН – серединный перпендикуляр к ЕТ. Аналогично, СМ – серединный перпендикуляр к ТУ и АК - серединный перпендикуляр к УЕ.
Cлайд 10
Доказательство: следовательно, D – середина ВС.
