X
Код презентации скопируйте его
От египетского треугольника до Пифагора
Скачать эту презентацию
Презентация на тему От египетского треугольника до Пифагора
Скачать эту презентациюCлайд 1
От египетского треугольника до Пифагора Автор Янченко Т.Л. Август 9, 2004
Cлайд 2
Cлайд 3
Древний Египет В 23 веке до н.э. был известен прямоугольный треугольник со сторонами 3,4,5.Это единственная тройка последовательных чисел, для которых верно равенство 32+42=52.
Cлайд 4
Cлайд 5
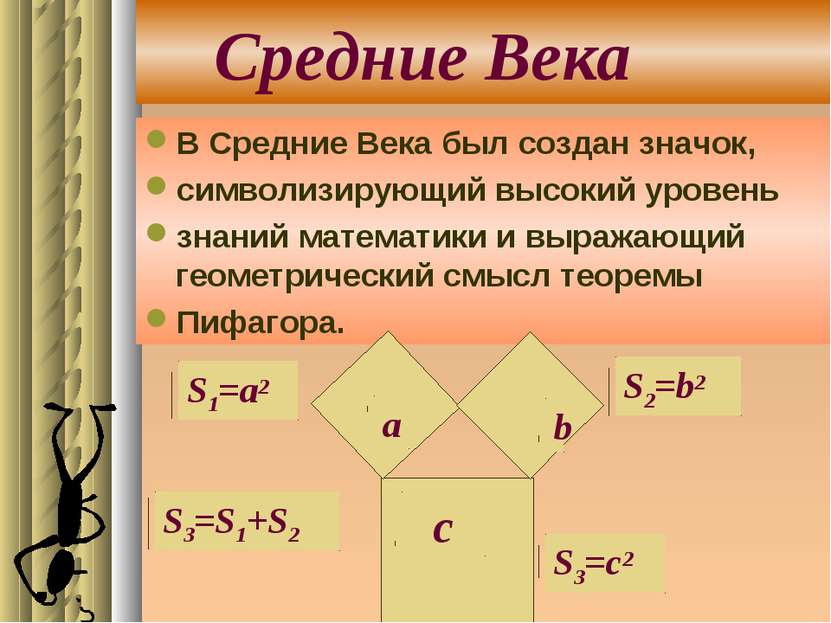
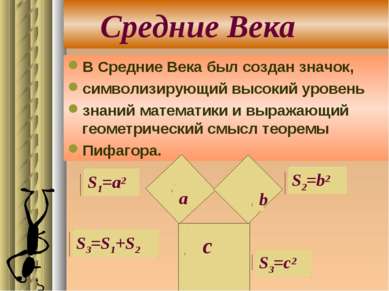
Древний Китай В 11 веке до н.э.был известен рисунок,дающий геометрическое доказательство т. Пифагора. с a b S1=c2 S2=(a-b)2 S3=4ab/2 S1=S2+S3 c2=(a-b)2+2ab c2=a2+b2
Cлайд 6
Cлайд 7
Древняя Индия С глубокой древности при строительстве храмов иконостас располагался строго на востоке. Для определения направления на восток использовались самая длинная тень от вертикального стержня(юг) и ей перпендикулярное направление(восток), для чего применялся прямоугольный треугольник со сторонами 15, 36, 39, известный в 7 веке до н.э. :152+362=392.
Cлайд 8
Cлайд 9
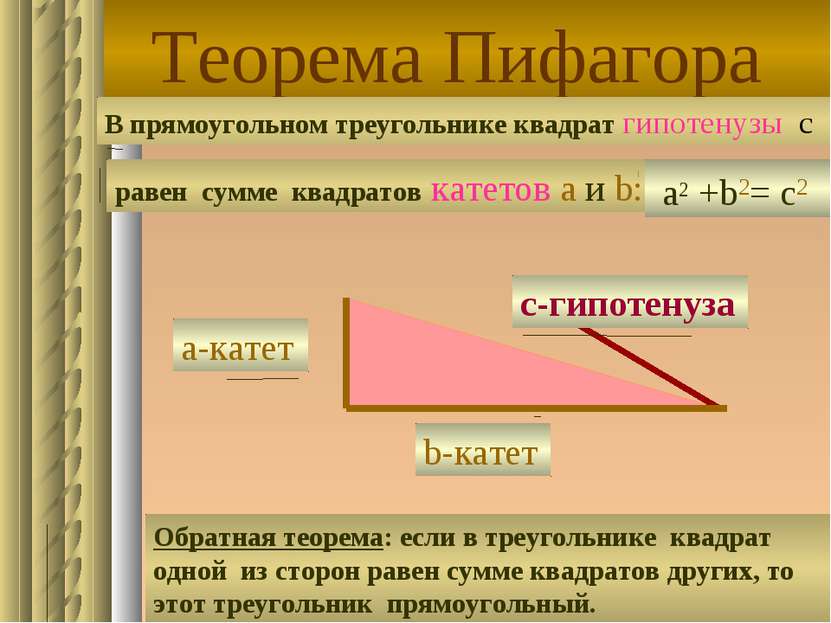
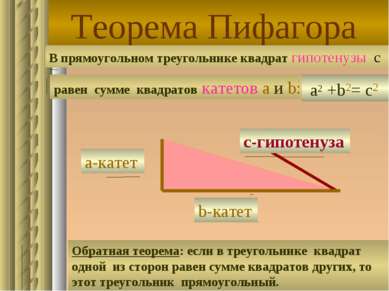Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы с равен сумме квадратов катетов а и b: с-гипотенуза а-катет b-катет а2 +b2= c2 Обратная теорема: если в треугольнике квадрат одной из сторон равен сумме квадратов других, то этот треугольник прямоугольный.
Cлайд 10
Средние Века В Средние Века был создан значок, символизирующий высокий уровень знаний математики и выражающий геометрический смысл теоремы Пифагора. S1=a2 S2=b2 S3=c2 a b c S3=S1+S2
Cлайд 11
Карикатуры Значок теоремы Пифагора породил ряд карикатур.
Cлайд 12
Карикатуры
