X
Код презентации скопируйте его
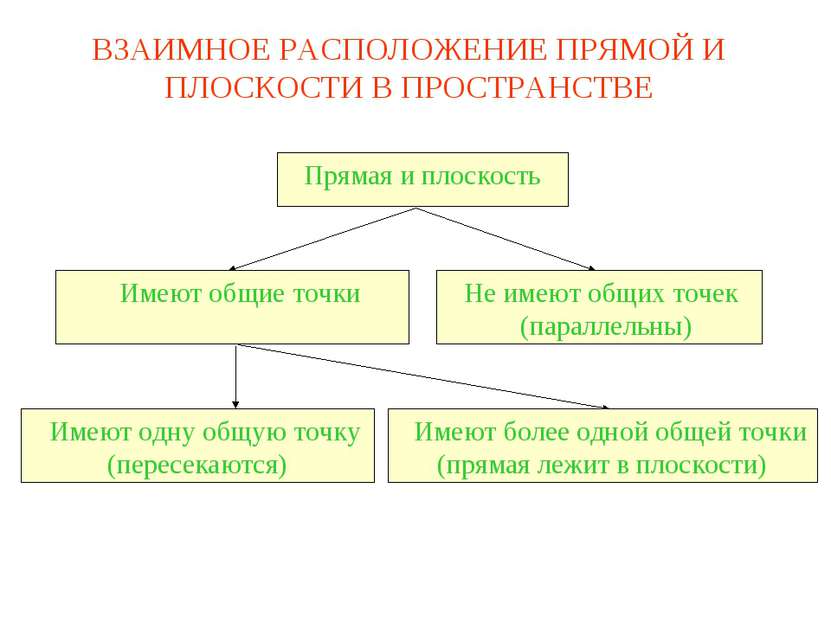
Параллельность прямой и плоскости
Скачать эту презентацию
Презентация на тему Параллельность прямой и плоскости
Скачать эту презентациюCлайд 1
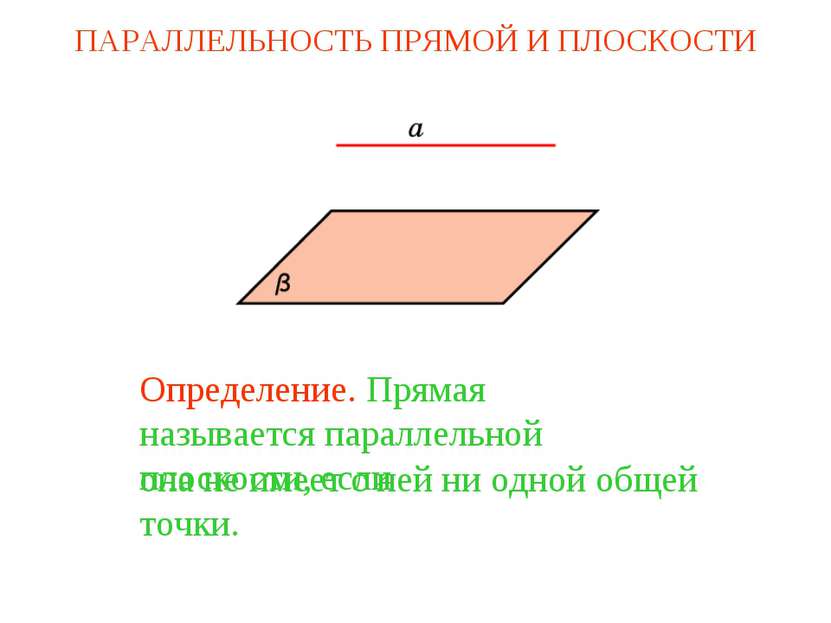
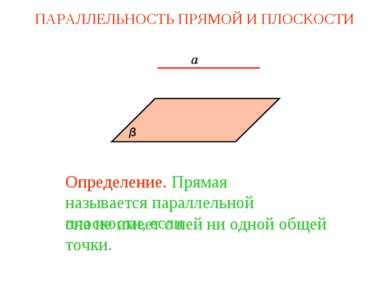Определение. Прямая называется параллельной плоскости, если она не имеет с ней ни одной общей точки. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Cлайд 2
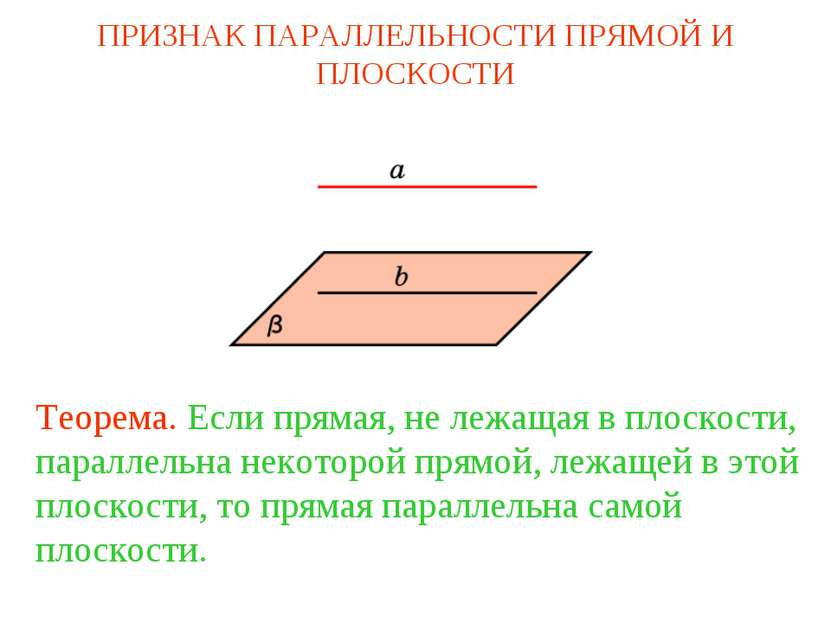
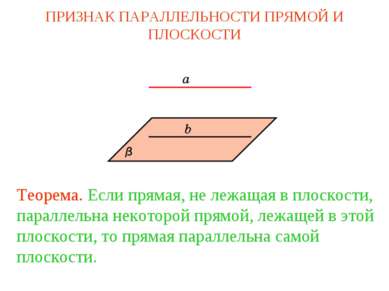Теорема. Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то прямая параллельна самой плоскости. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Cлайд 3
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
Cлайд 4
Верно ли утверждение о том, что две прямые, параллельные одной и той же плоскости, параллельны между собой? Ответ: Нет. Вопрос 1
Cлайд 5
Верно ли утверждение: "Прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости"? Ответ: Нет. Вопрос 2
Cлайд 6
Одна из двух параллельных прямых параллельна плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости? Ответ: Нет. Вопрос 3
Cлайд 7
Даны две параллельные прямые. Через каждую из них проведена плоскость. Эти две плоскости пересекаются. Как расположена их линия пересечения относительно данных прямых? Ответ: Параллельна. Вопрос 4
Cлайд 8
Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым? Ответ: Да. Вопрос 5
Cлайд 9
Сторона AF правильного шестиугольника ABCDEF лежит в плоскости α, не совпадающей с плоскостью шестиугольника. Как расположены остальные стороны ABCDEF относительно плоскости α? Ответ: AB, BC, DE, EF пересекают плоскость; CD параллельна плоскости. Упражнение 1
Cлайд 10
б) CDD1, A1C1D; В кубе A…D1 укажите плоскости, проходящие через вершины куба, параллельные прямой: а) AA1; б) AB1; в) AC1. Ответ: а) BCC1, CDD1, BDD1; в) нет. Упражнение 2
Cлайд 11
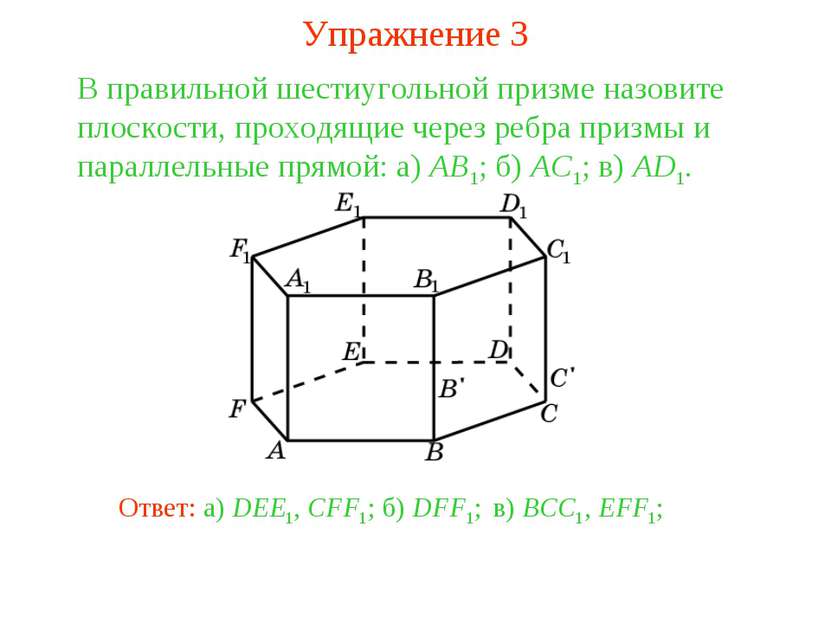
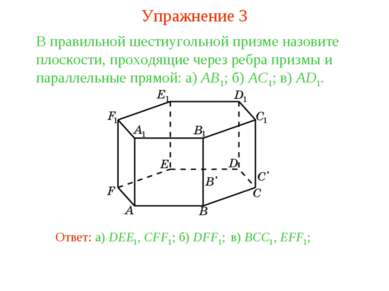в) BCC1, EFF1; В правильной шестиугольной призме назовите плоскости, проходящие через ребра призмы и параллельные прямой: а) AB1; б) AC1; в) AD1. б) DFF1; Ответ: а) DEE1, CFF1; Упражнение 3
Cлайд 12
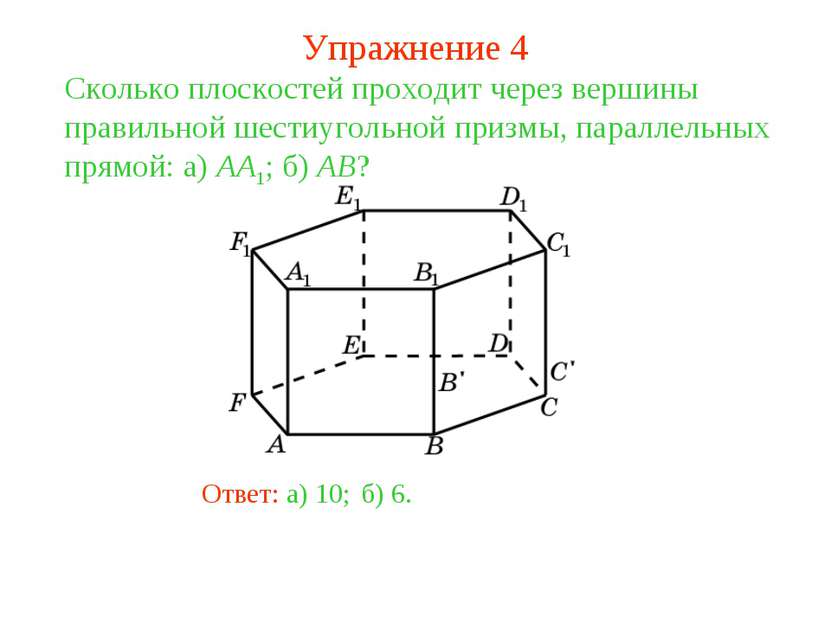
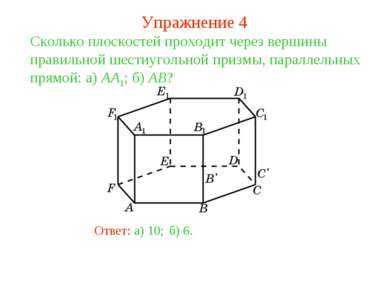Ответ: а) 10; Сколько плоскостей проходит через вершины правильной шестиугольной призмы, параллельных прямой: а) AA1; б) AB? б) 6. Упражнение 4
Cлайд 13
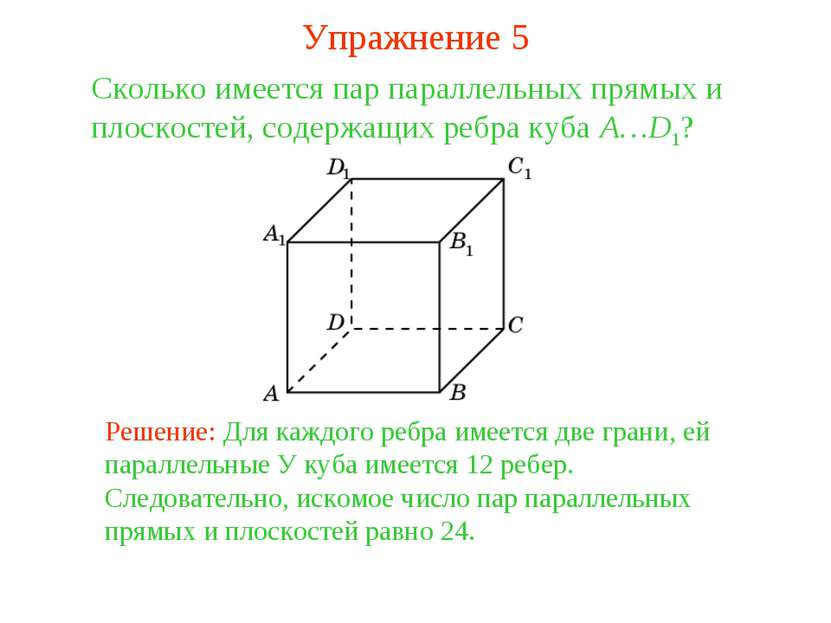
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра куба A…D1? Решение: Для каждого ребра имеется две грани, ей параллельные У куба имеется 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24. Упражнение 5
Cлайд 14
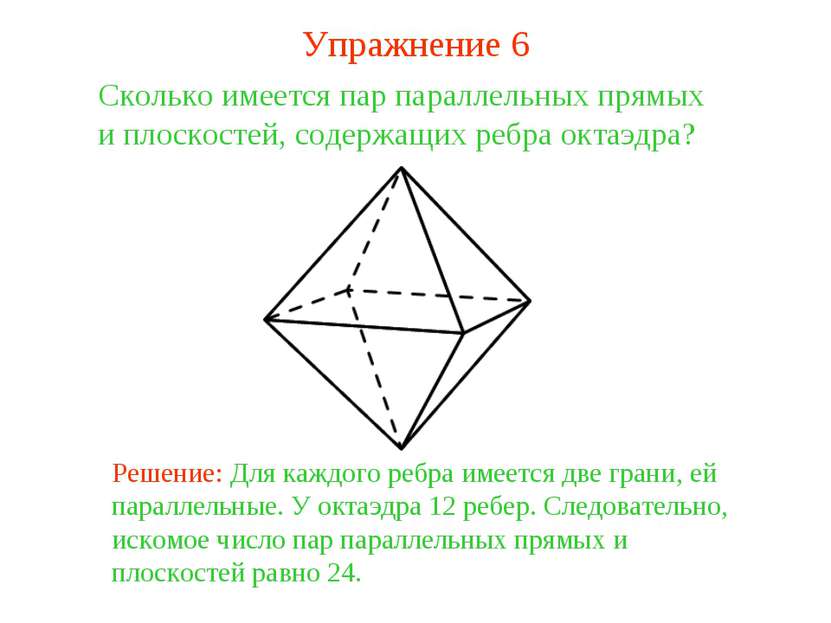
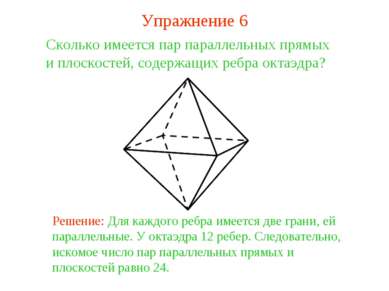Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра октаэдра? Решение: Для каждого ребра имеется две грани, ей параллельные. У октаэдра 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24. Упражнение 6
Cлайд 15
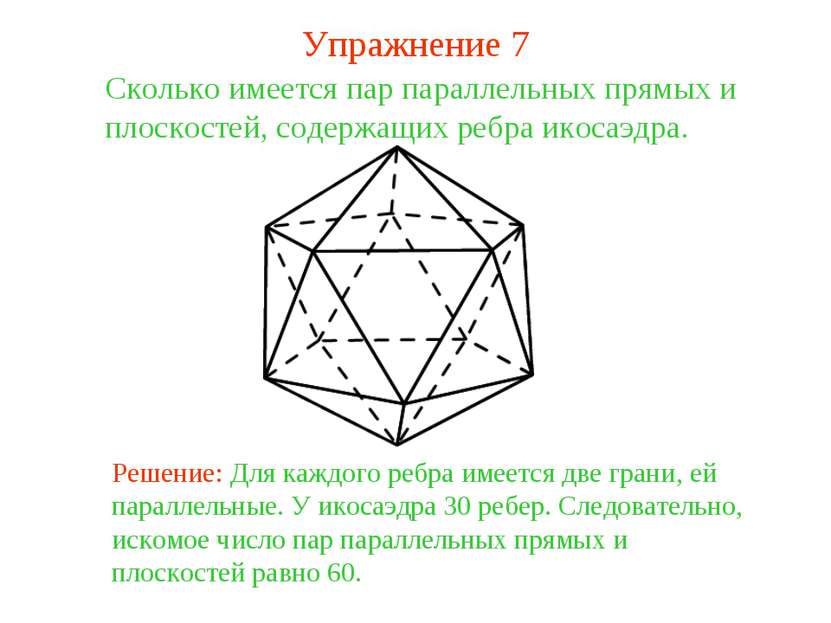
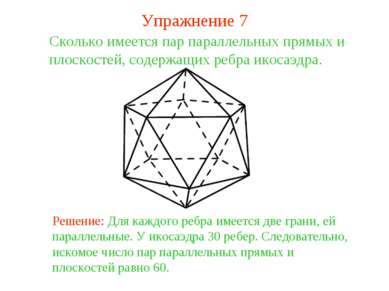Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра икосаэдра. Решение: Для каждого ребра имеется две грани, ей параллельные. У икосаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 60. Упражнение 7
Cлайд 16
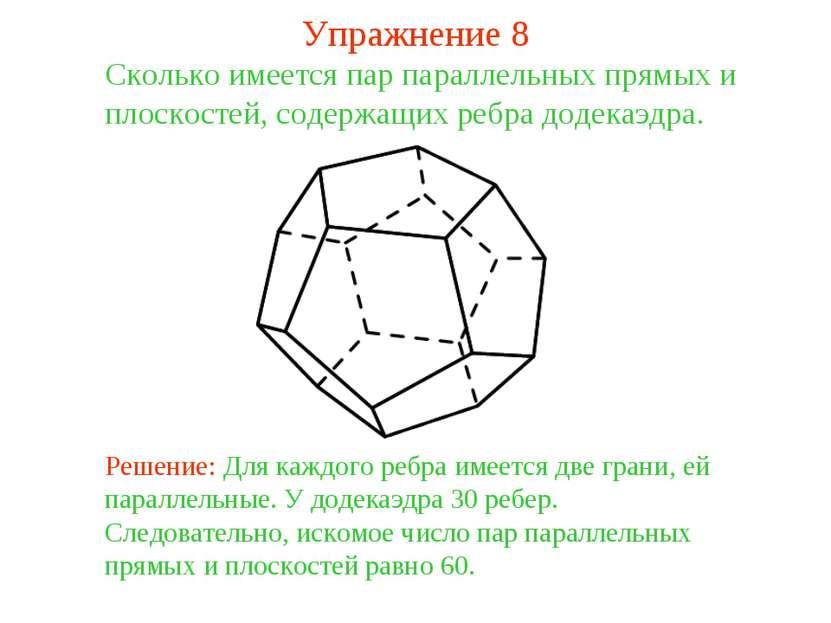
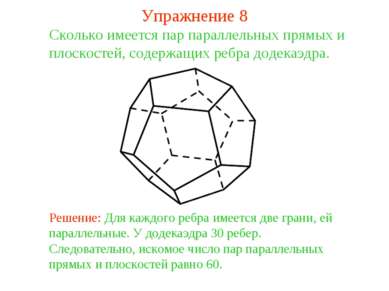Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра додекаэдра. Решение: Для каждого ребра имеется две грани, ей параллельные. У додекаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 60. Упражнение 8
Cлайд 17
Даны две скрещивающиеся прямые. Как через одну из них провести плоскость, параллельную другой? Решение: Через точку одной прямой провести прямую, параллельную второй данной прямой. Затем через полученные пересекающиеся прямые провести плоскость. Она будет параллельна второй данной прямой. Упражнение 9
Cлайд 18
В основании четырехугольной пирамиды SABCD лежит параллелограмм. Каково взаимное расположение прямой пересечения плоскостей граней SAB и SCD и плоскости основания ABCD? Ответ: Параллельны. Упражнение 10
