X
Код презентации скопируйте его
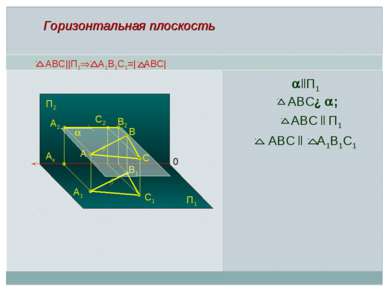
Положение плоскости относительно плоскостей проекций
Скачать эту презентацию
Презентация на тему Положение плоскости относительно плоскостей проекций
Скачать эту презентациюCлайд 1
Положение плоскости относительно плоскостей проекций
Cлайд 2
Плоскости частного положения
Cлайд 3
Плоскость, перпендикулярная к плоскости проекций, называется проецирующей Особенности проецирующих плоскостей: – одна проекция любого элемента, расположенного – в проецирующей плоскости, совпадает с соответствующим следом этой плоскости – угол наклона заданной плоскости к плоскости проекций на эпюре проецируется в натуральную величину Проецирующие плоскости
Cлайд 4
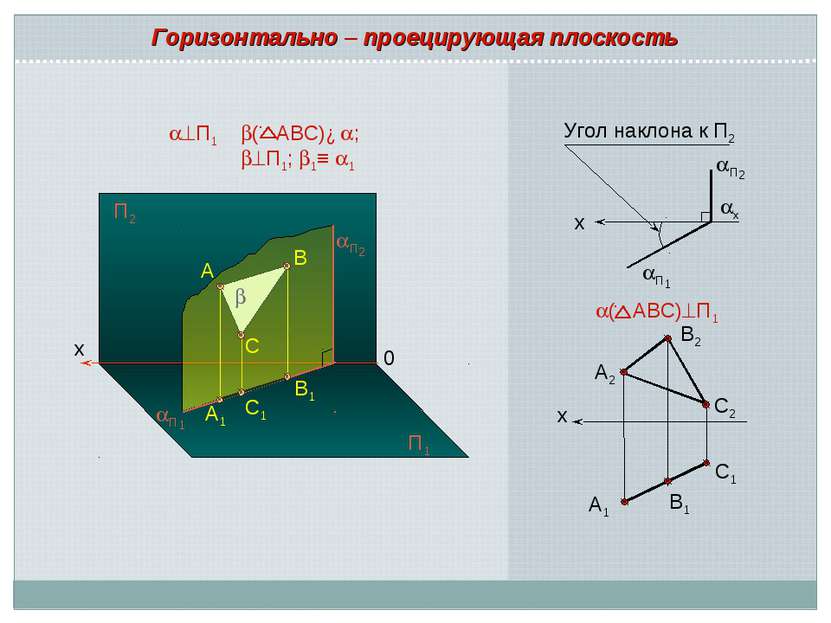
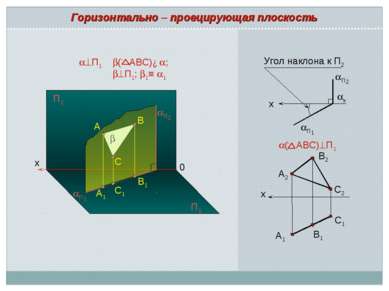х А2 В2 С2 С1 А1 В1 ( АВС) П1 Горизонтально – проецирующая плоскость x П1 x Угол наклона к П2 x A1 B1 A 0 B C П2 С1 П2 П1 П1 ( АВС)∈ ; П1; 1≡ 1 П1 П2
Cлайд 5
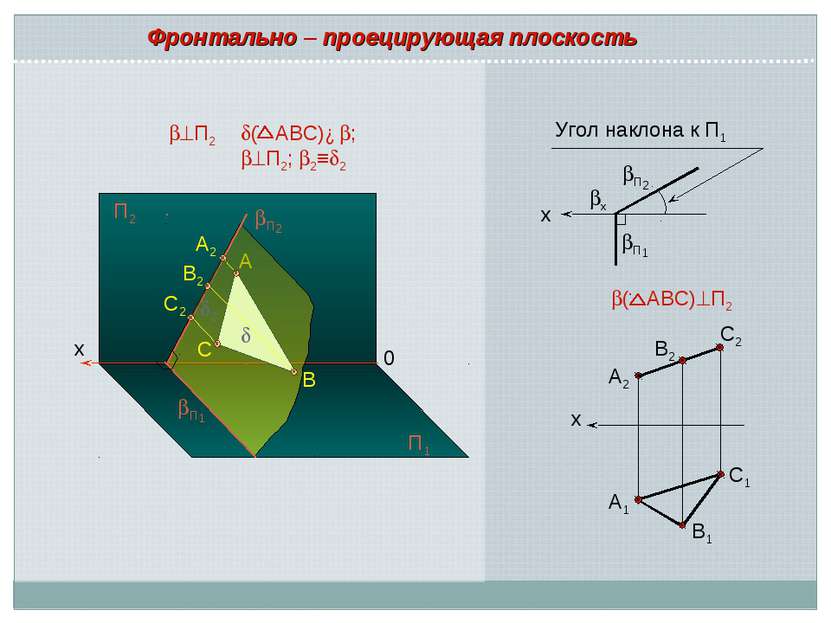
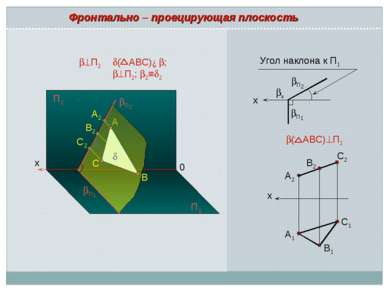x A2 B2 A 0 B C П2 П1 С2 П2 П1 П2 ( АВС)∈ ; П2; 2≡ 2 х А2 В2 С2 С1 А1 В1 ( АВС) П2 x П1 П2 x Угол наклона к П1 Фронтально – проецирующая плоскость 2
Cлайд 6
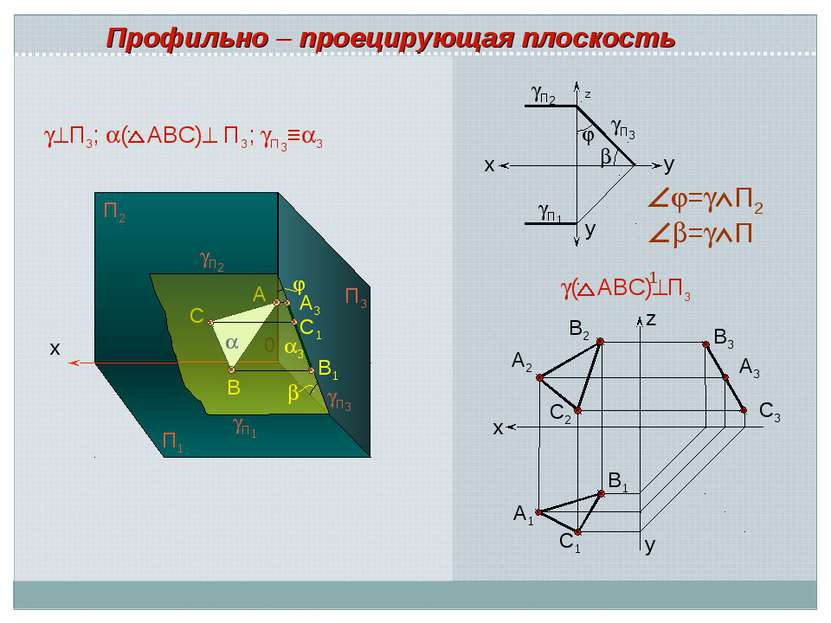
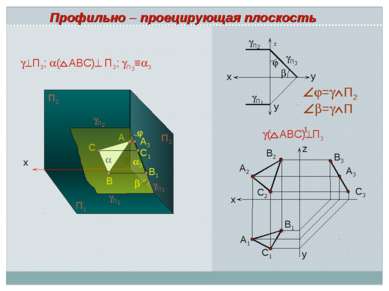x A 0 B C П2 П1 П2 П1 A3 С1 B1 П3 х А3 В3 С3 С1 А1 В1 В2 А2 С2 ( АВС) П3 Профильно – проецирующая плоскость z y x П1 П2 П3 z у у = П2 = П1 П3 3 П3; ( АВС) П3; П3≡ 3
Cлайд 7
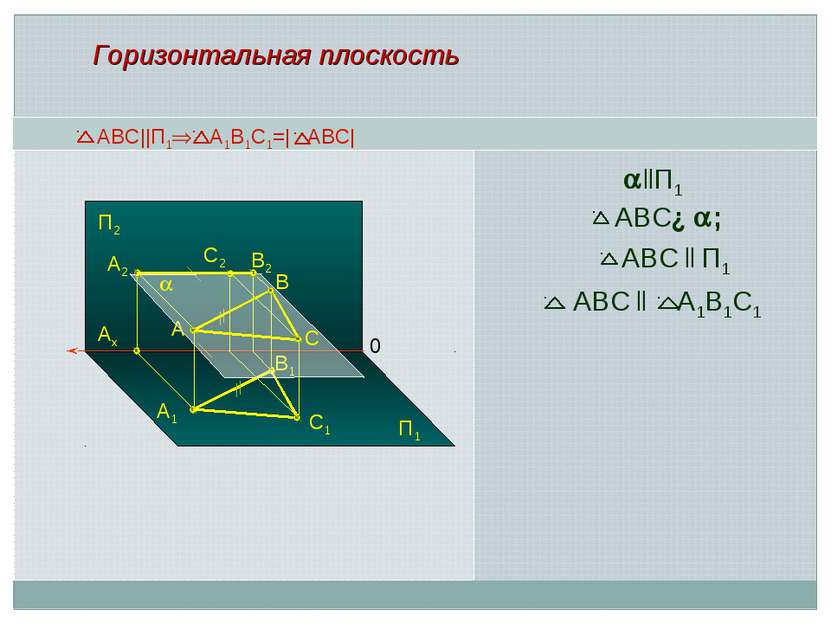
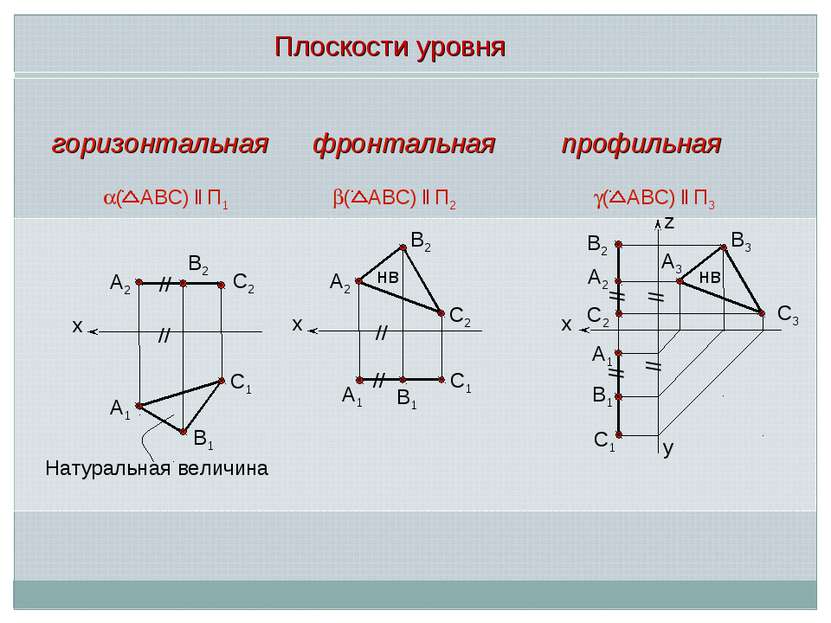
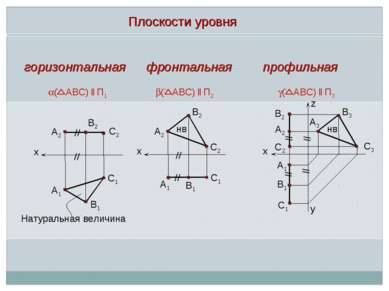
Плоскость, параллельная к плоскости проекций, называется плоскостью уровня Особенности плоскостей уровня: Плоскости уровня – любая плоская фигура, расположенная в плоскости уровня, проецируется на параллельную ей плоскость проекций без искажения, – т.е. в натуральную величину
Cлайд 8
АВС||П1 А1В1С1=| АВС| A1 B1 A A2 Ax 0 B B2 llП1 С1 С2 Горизонтальная плоскость П2 П1 АВС∈ ; АВС ll П1 АВС ll А1В1С1 С
Cлайд 9
Плоскости уровня х А2 В2 С2 С1 А1 В1 х А2 В2 С2 С1 А1 В1 х А3 В3 С3 С1 А1 В1 // // ( АВС) ll П1 Натуральная величина // // нв ( АВС) ll П2 В2 А2 С2 // // // // ( АВС) ll П3 нв горизонтальная фронтальная профильная z y
