X
Код презентации скопируйте его
Параллельность прямой и плоскости
Скачать эту презентацию
Презентация на тему Параллельность прямой и плоскости
Скачать эту презентациюCлайд 1
Творческий проект выполнил: ученик 10 класса МОУ СОШ № 22 г.Твери Бербеков Данила "Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей" Руководитель проекта Учитель математики МОУ СОШ № 22 г. Твери Синицына Жанна Анатольевна Творческий проект по теме:
Cлайд 2
Начнём по порядку . что же такое стереометрия? Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Cлайд 3
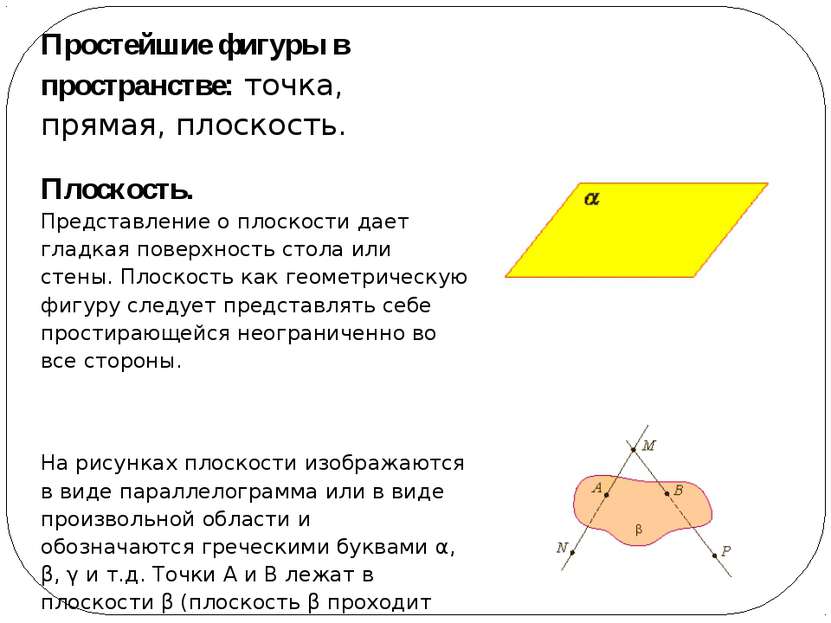
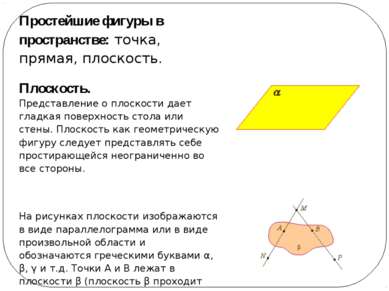Простейшие фигуры в пространстве: точка, прямая, плоскость. Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
Cлайд 4
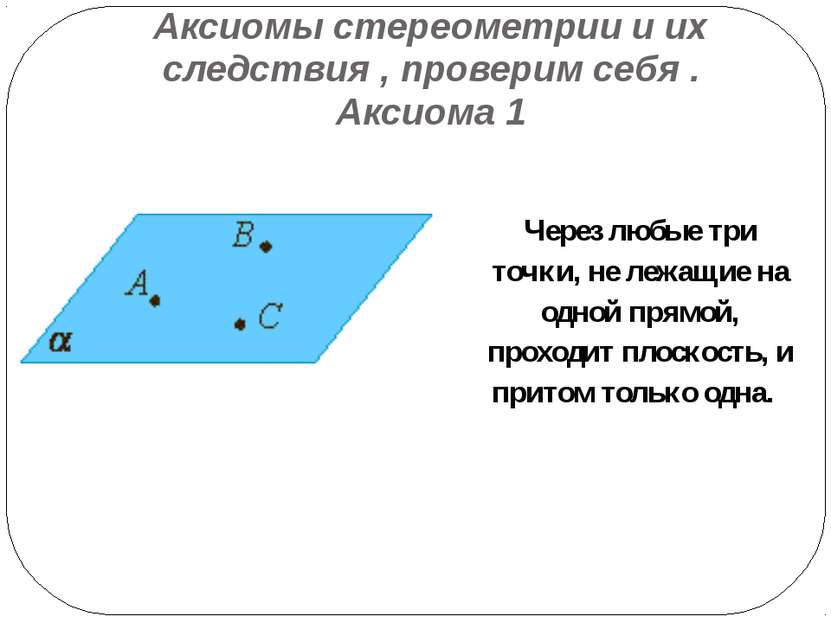
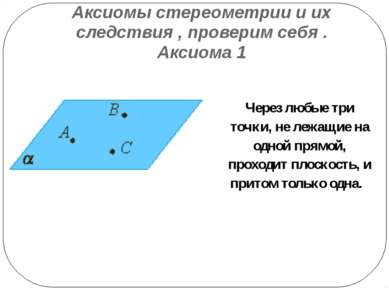Аксиомы стереометрии и их следствия , проверим себя . Аксиома 1 Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Cлайд 5
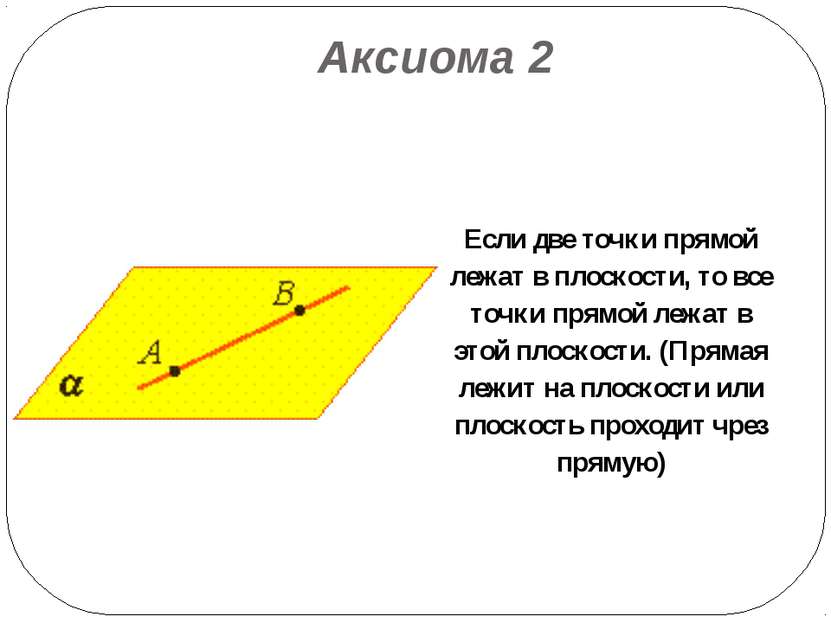
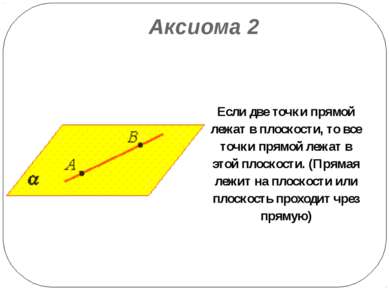Аксиома 2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит чрез прямую)
Cлайд 6
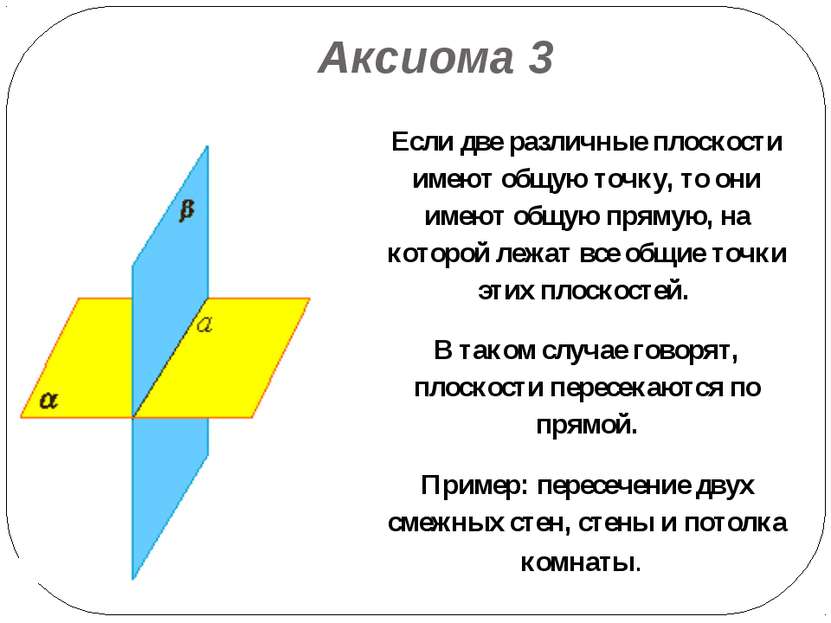
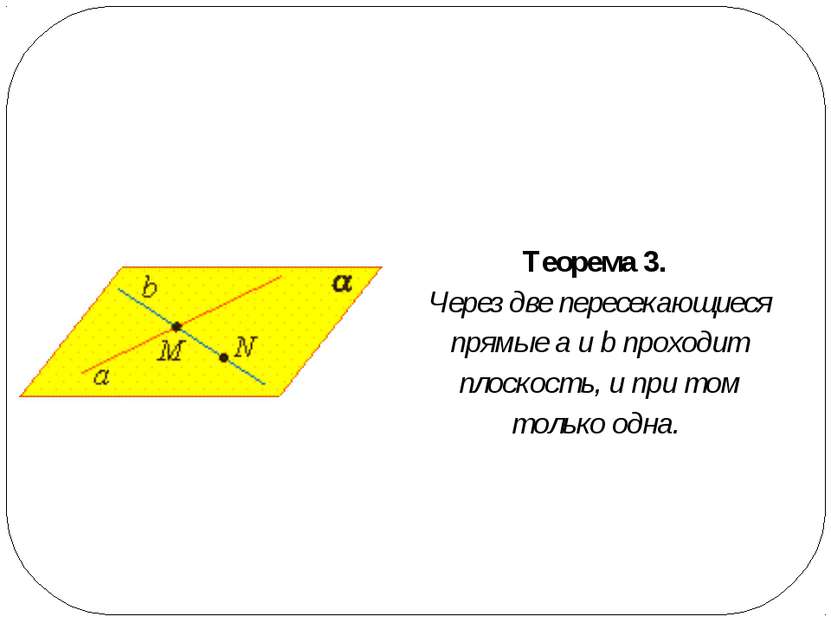
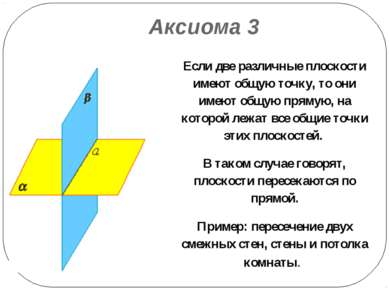Аксиома 3 Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты.
Cлайд 7
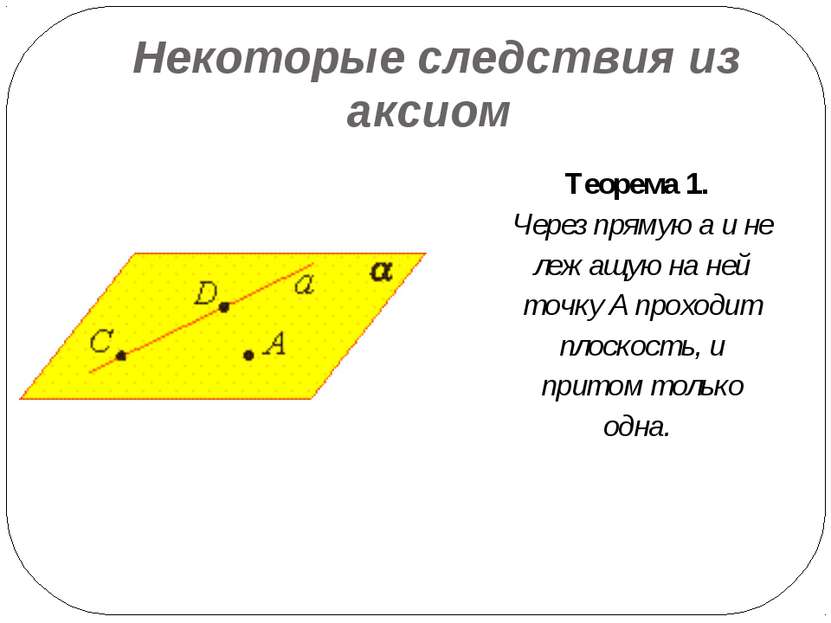
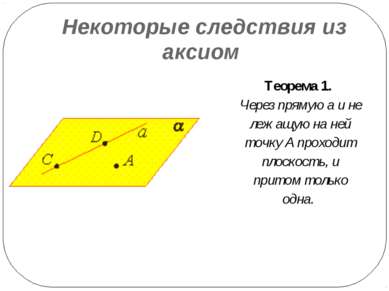Некоторые следствия из аксиом Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
Cлайд 8
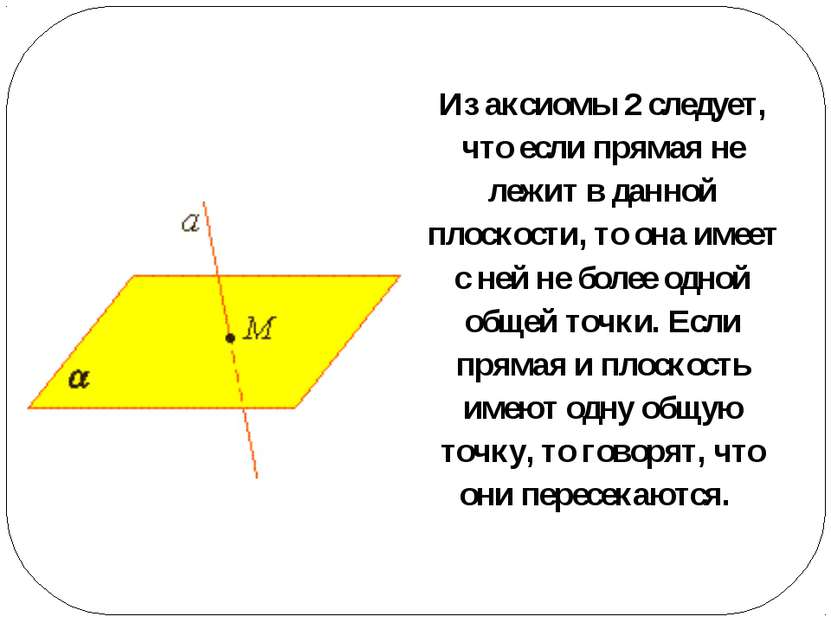
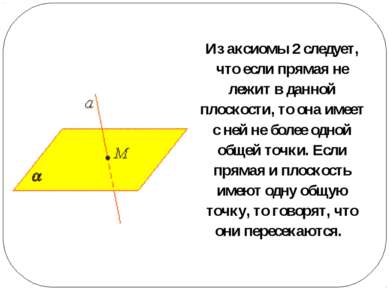Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Cлайд 9
Теорема 3. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
Cлайд 10
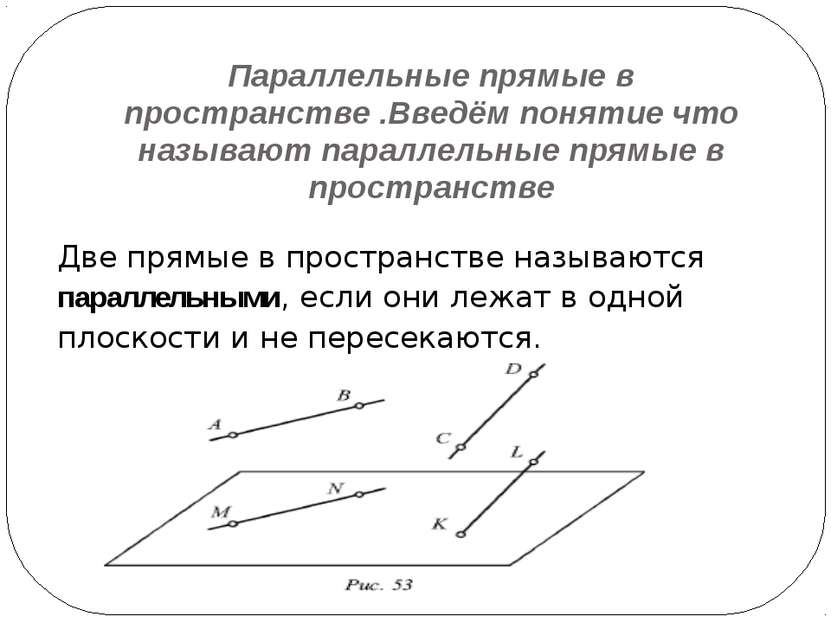
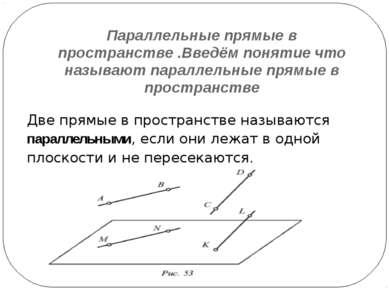Параллельные прямые в пространстве .Введём понятие что называют параллельные прямые в пространстве Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Cлайд 11
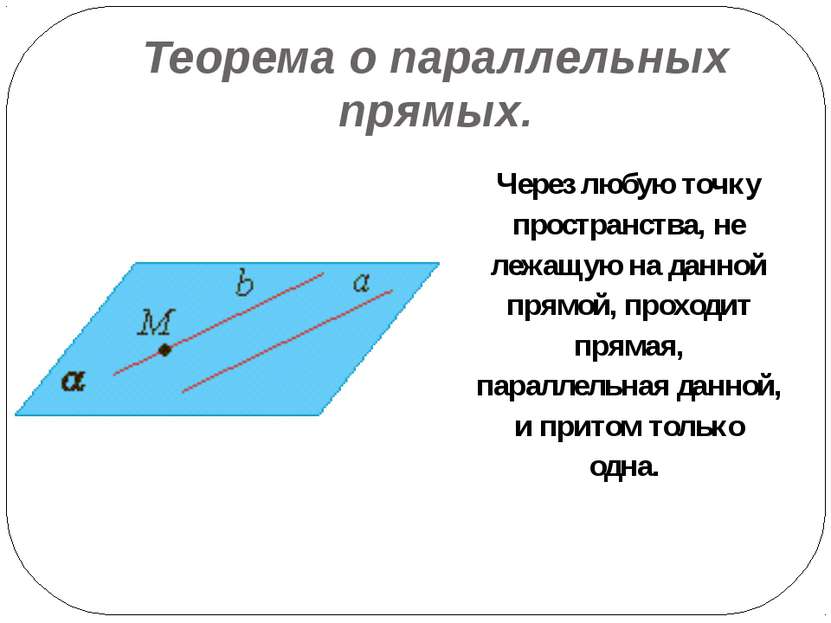
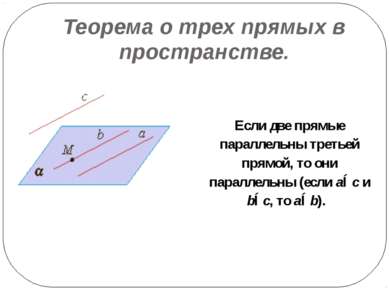
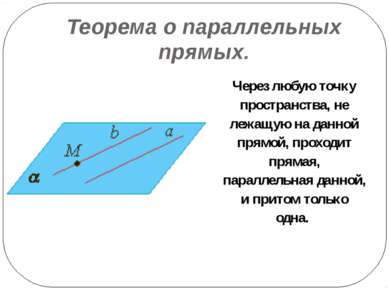Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Cлайд 12
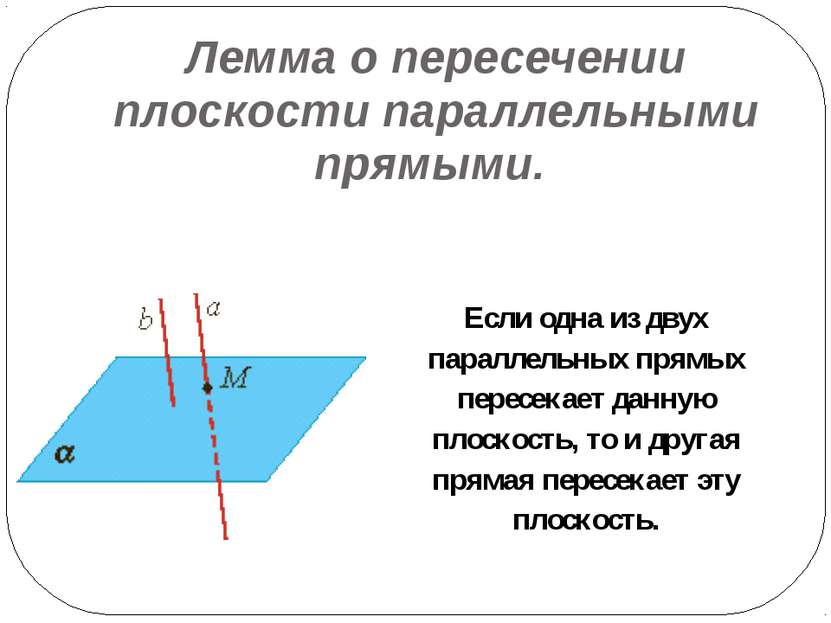
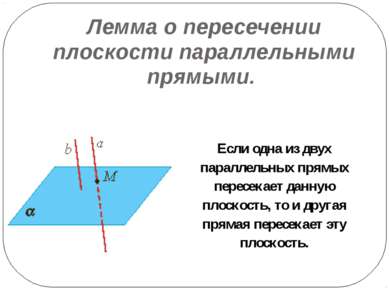Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Cлайд 13
Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).
Cлайд 14
Спасибо за внимание!
