X
Код презентации скопируйте его
Точки на прямой
Скачать эту презентацию
Презентация на тему Точки на прямой
Скачать эту презентациюCлайд 1
Точки на прямой В качестве аксиомы взаимного расположения точек на прямой принимается следующее свойство.
Cлайд 2
Отрезок Отрезком называется часть прямой, состоящая из двух данных точек и всех точек, лежащих между ними. При этом сами данные точки называются концами отрезка. Отрезок обозначается указанием его концов.
Cлайд 3
Луч Для обозначения лучей используются пары прописных латинских букв, например, AB, первая из которых обозначает начало луча, а вторая - какую-нибудь точку, принадлежащую лучу.
Cлайд 4
Вопрос 1 Какое свойство принимается в качестве аксиомы взаимного расположения точек на прямой? Ответ: Каждая точка на прямой разбивает эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки, а точки из одной части лежат по одну сторону от данной точки.
Cлайд 5
Вопрос 2 Какая фигура называется отрезком? Ответ: Отрезком называется часть прямой, состоящая из двух данных точек и всех точек, лежащих между ними.
Cлайд 6
Вопрос 3 Как обозначается отрезок? Ответ: Отрезок обозначается указанием его концов.
Cлайд 7
Вопрос 4 Какая фигура называется лучом? Ответ: Лучом называется часть прямой, состоящая из данной точки и всех точек, лежащих от нее по одну сторону.
Cлайд 8
Вопрос 5 Как обозначаются лучи? Ответ: Для обозначения лучей используются пары прописных латинских букв, например, AB, первая из которых обозначает начало луча, а вторая - какую-нибудь точку, принадлежащую лучу.
Cлайд 9
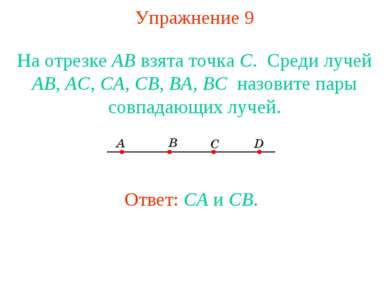
Упражнение 1 Между какими точками лежит точка D на рисунке? Ответ: E и F, C и F, A и F, O и F, B и F.
Cлайд 10
Упражнение 2 Какие точки лежат по одну сторону от точки A на рисунке? Ответ: E и C; O, B, D и F.
Cлайд 11
Упражнение 3 Для точек A, B, C, D прямой известно, что точки В и С лежат по одну сторону от точки А, точки В и D тоже лежат по одну сторону от точки А. Как расположены точки С и D относительно точки А?
Cлайд 12
Упражнение 4 На сколько частей делят прямую: а) одна точка? б) две точки? две; три; в) три точки? четыре; г) n точек? n + 1.
Cлайд 13
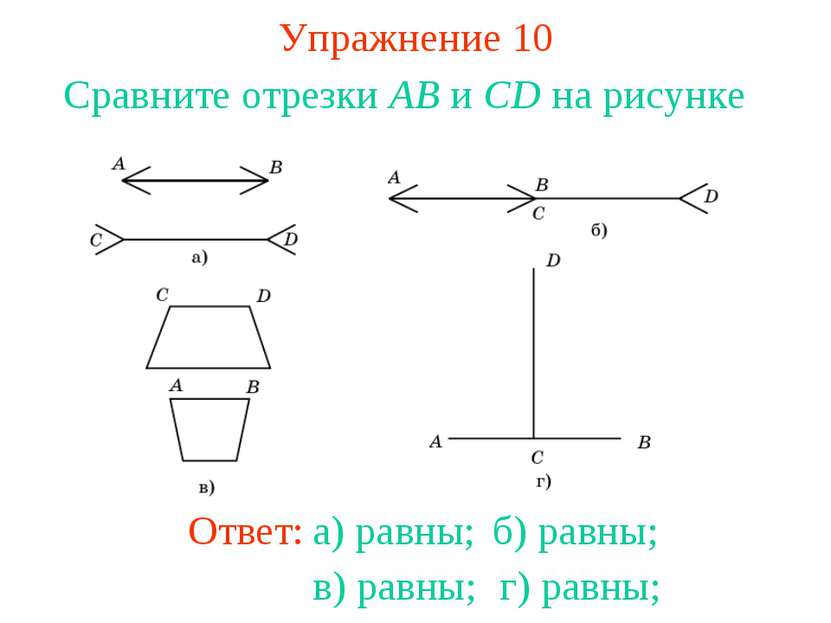
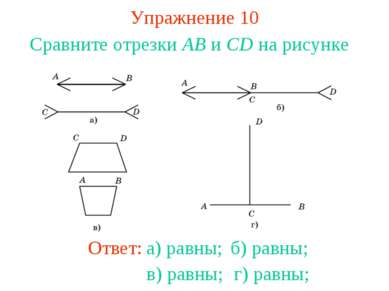
Упражнение 5 Назовите отрезки, изображенные на рисунках: а), б). Ответ: а) AB, AC, BC; б) AB, AC, AD, BC, BD, CD.
Cлайд 14
Упражнение 6 Для точек A, B прямой укажите, где расположены точки C, для которых выполняются равенства: а) AC + BC = AB; б) AC – BC = AB; в) BC – AC = AB. б) точки, лежащие от B по другую сторону, чем точка A; в) точки, лежащие от A по другую сторону, чем точка B.
Cлайд 15
Упражнение 7 На прямой отмечены точки А, В, С, D. Выразите каждый из отрезков в виде суммы или разности остальных. Ответ: AB = AC – BC; AC = AB + BC; AD = AB + BC + CD; BC = BD – CD; BD = BC + CD; CD = BD – BC.
Cлайд 16
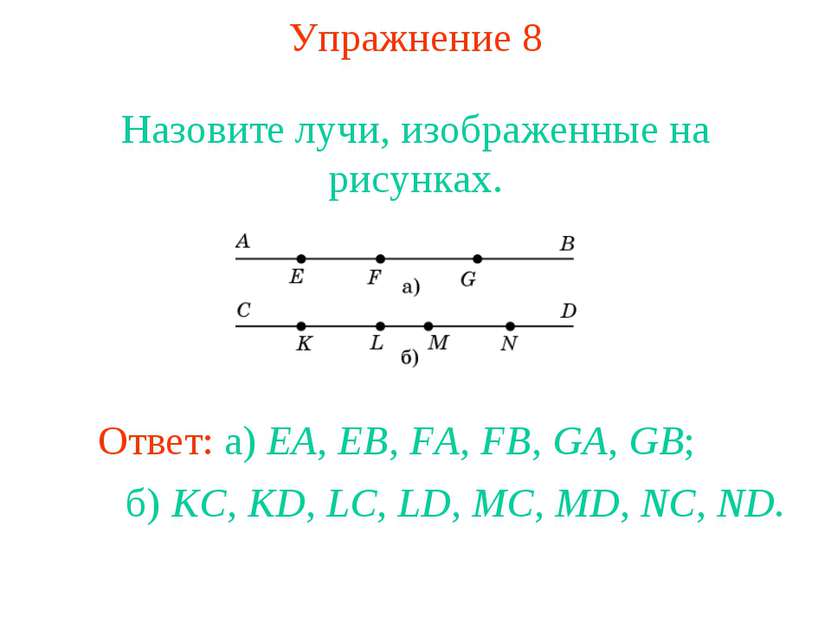
Упражнение 8 Назовите лучи, изображенные на рисунках. Ответ: а) EA, EB, FA, FB, GA, GB; б) KC, KD, LC, LD, MC, MD, NC, ND.
Cлайд 17
Упражнение 9 На отрезке АВ взята точка С. Среди лучей АВ, АС, СА, СВ, BA, BC назовите пары совпадающих лучей. Ответ: CA и CB.
Cлайд 18
Упражнение 10 Сравните отрезки AB и CD на рисунке б) равны; в) равны; г) равны;
Cлайд 19
Упражнение 11 Можно ли соединить пять точек плоскости отрезками так, чтобы каждая точка была соединена ровно с: а) двумя; б) тремя; в) четырьмя другими? б) нет; в) да.
