X
Код презентации скопируйте его
Расстояние от точки до плоскости в пространстве
Скачать эту презентацию
Презентация на тему Расстояние от точки до плоскости в пространстве
Скачать эту презентациюCлайд 1
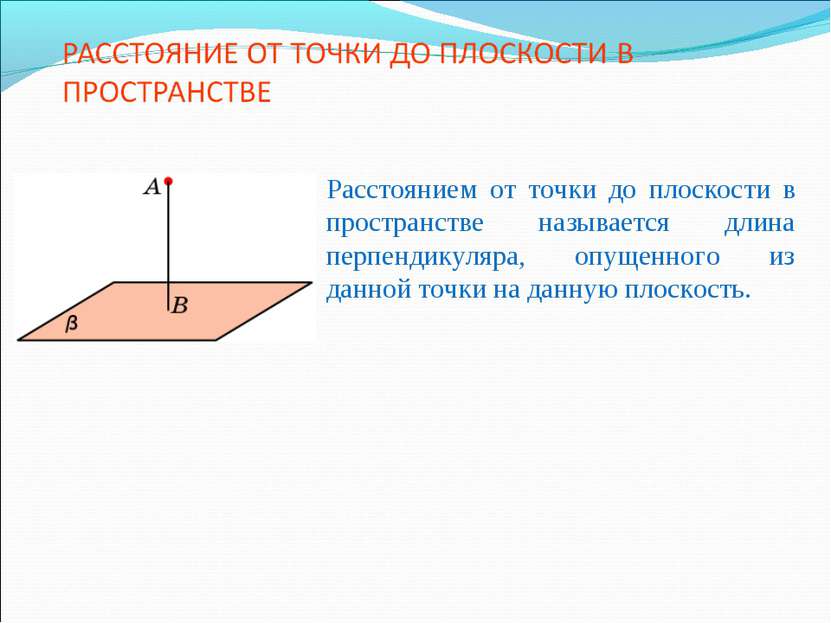
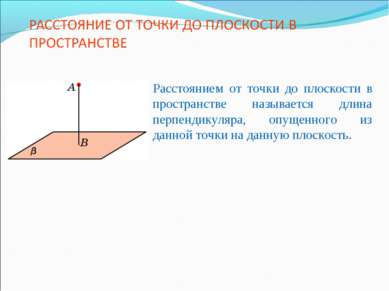Расстоянием от точки до плоскости в пространстве называется длина перпендикуляра, опущенного из данной точки на данную плоскость.
Cлайд 2
В правильном тетраэдре ABCD найдите расстояние от вершины D до плоскости ABC.
Cлайд 3
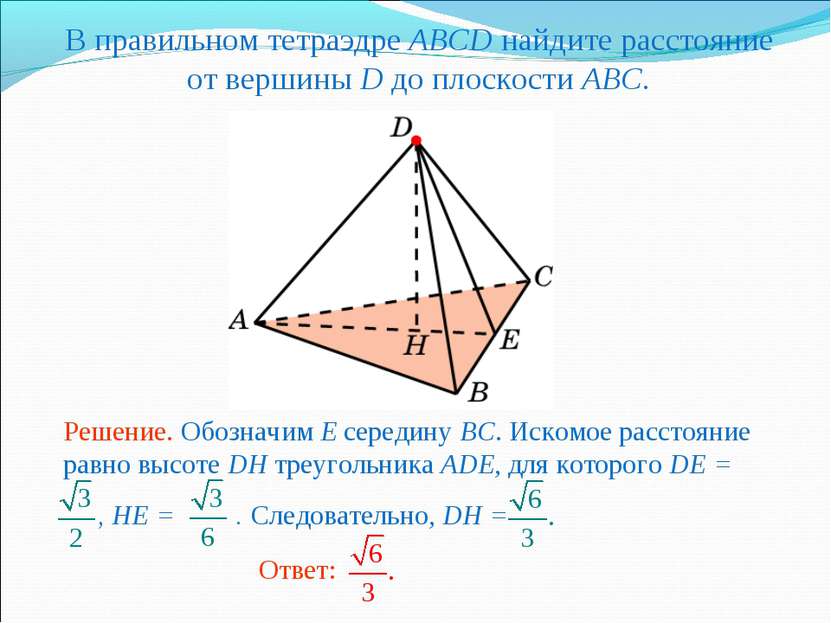
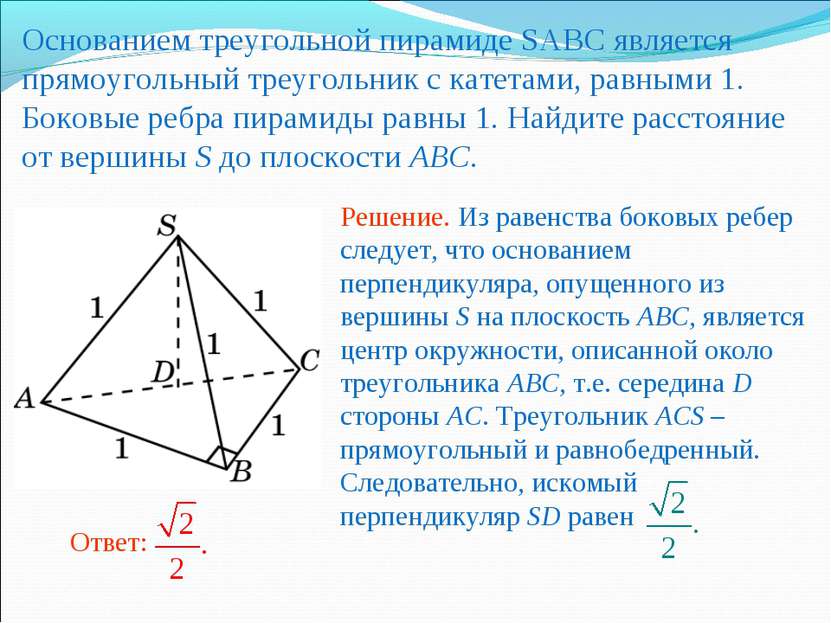
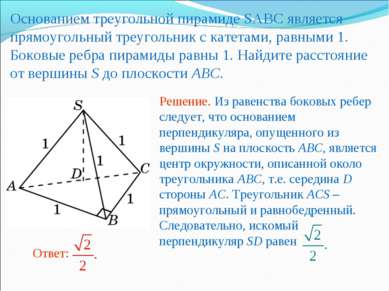Основанием треугольной пирамиде SABC является прямоугольный треугольник с катетами, равными 1. Боковые ребра пирамиды равны 1. Найдите расстояние от вершины S до плоскости ABC.
Cлайд 4
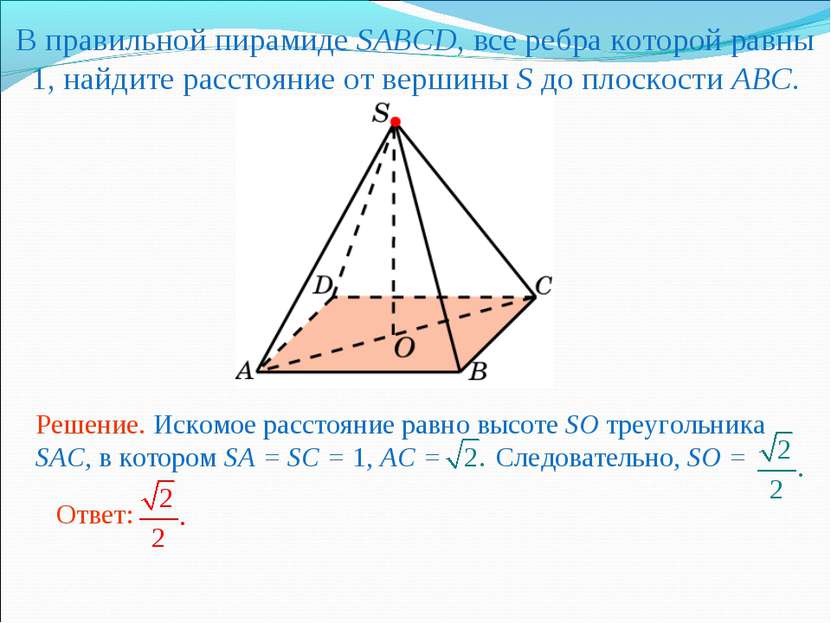
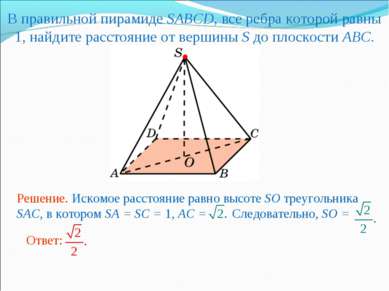В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от вершины S до плоскости ABC.
Cлайд 5
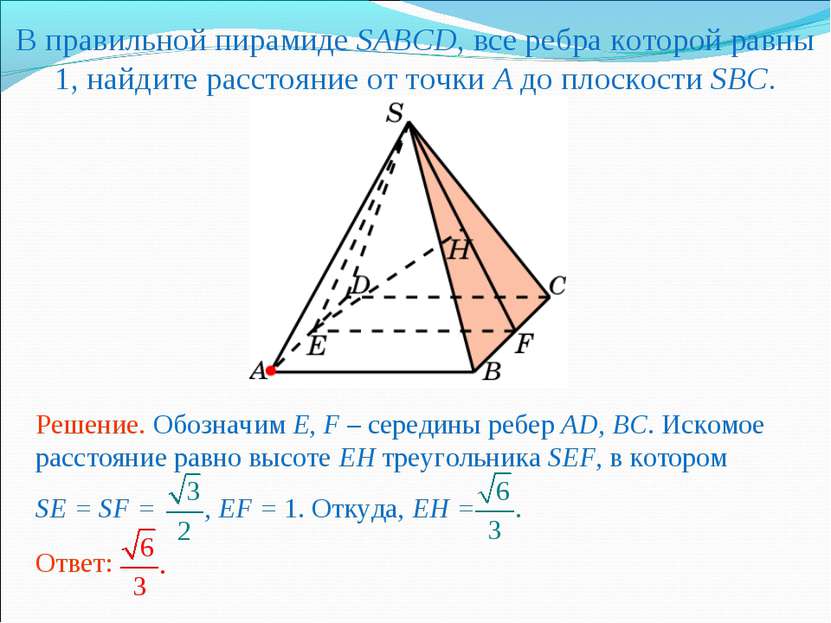
В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки A до плоскости SBC.
Cлайд 6
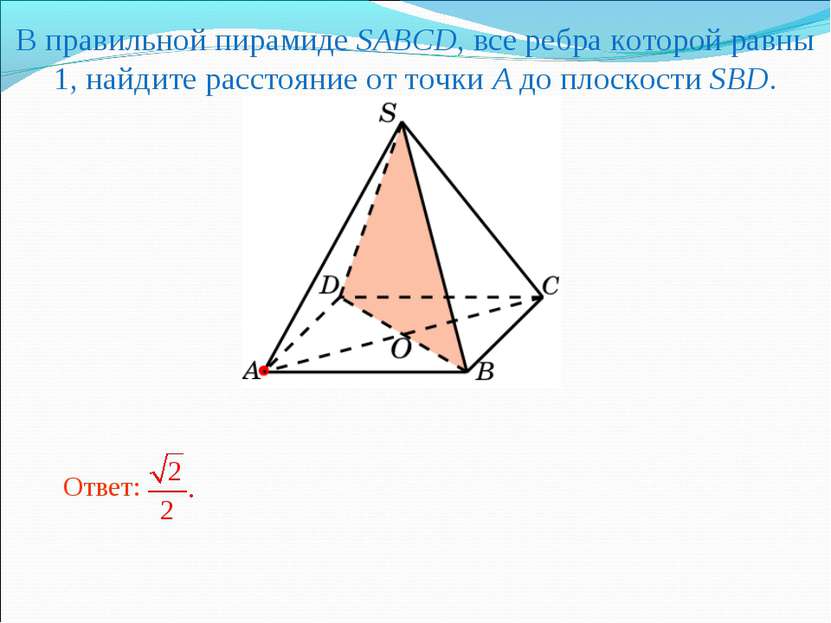
В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки A до плоскости SBD.
Cлайд 7
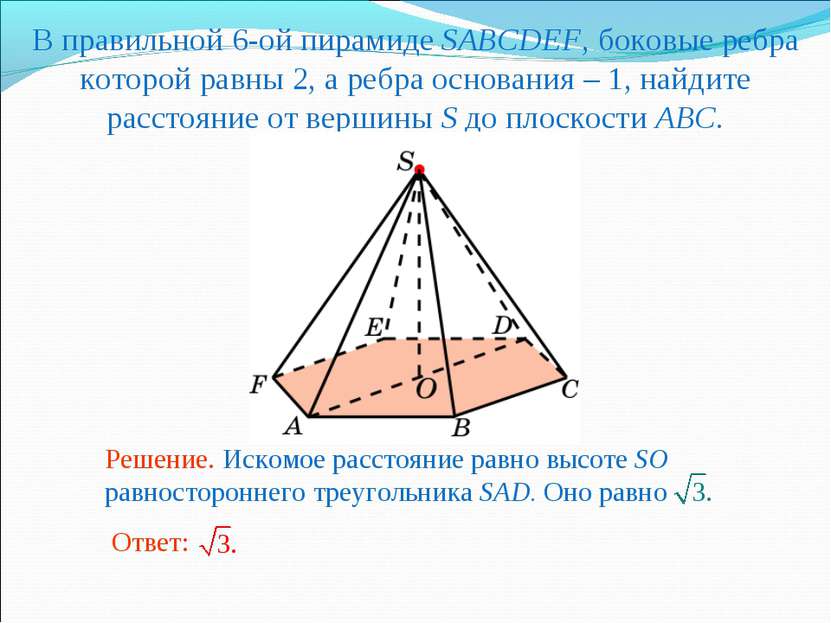
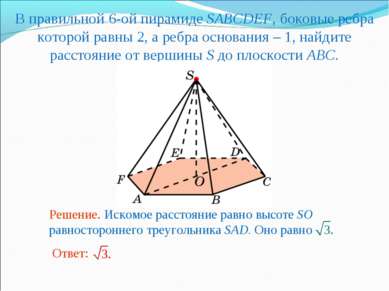В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от вершины S до плоскости ABC.
Cлайд 8
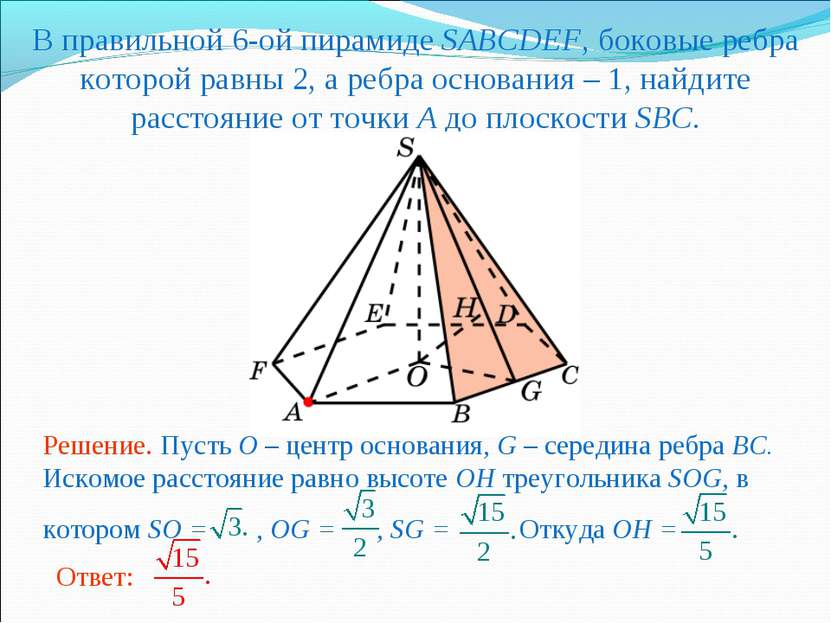
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SBC.
Cлайд 9
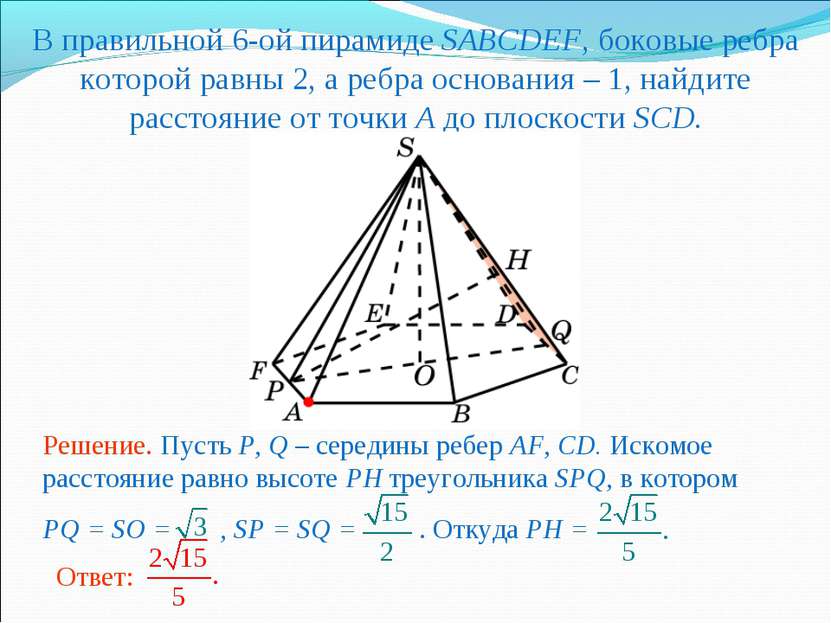
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SCD.
Cлайд 10
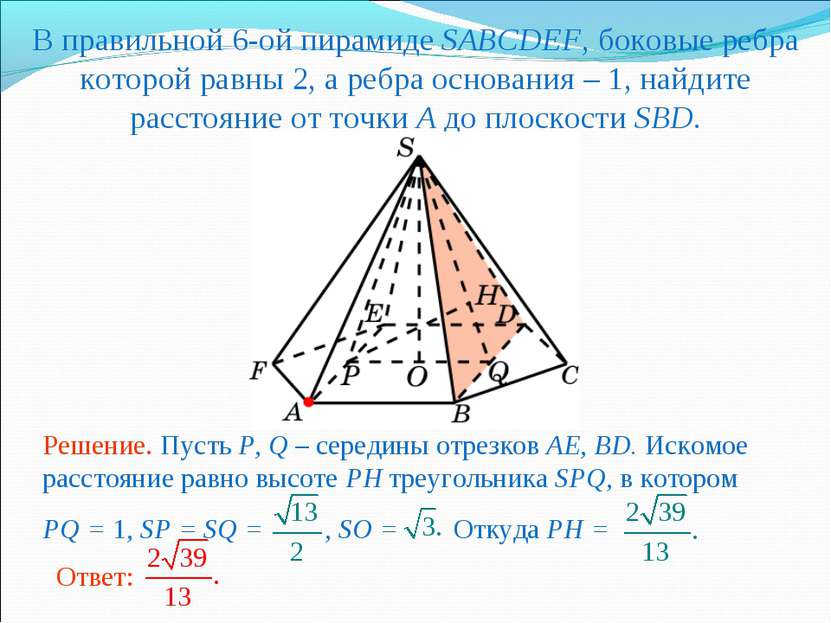
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SBD.
Cлайд 11
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SBE.
Cлайд 12
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SCE.
