X
Код презентации скопируйте его
Расстояние от точки до плоскости
Скачать эту презентацию
Презентация на тему Расстояние от точки до плоскости
Скачать эту презентациюCлайд 1
Cлайд 2
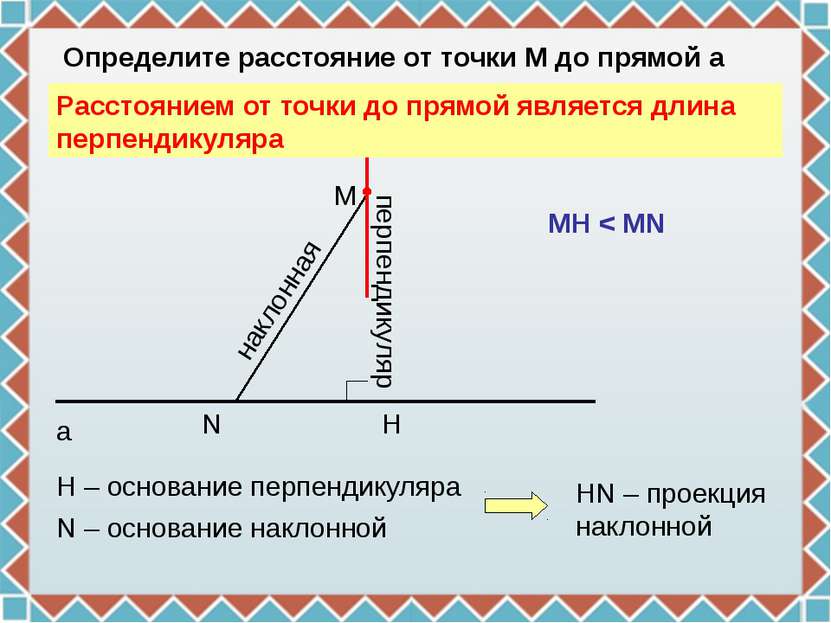
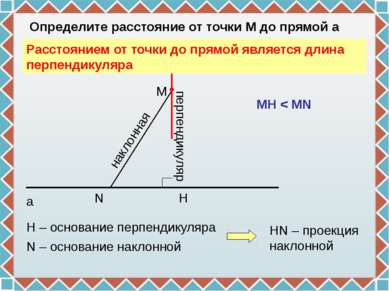N H M a Определите расстояние от точки М до прямой а перпендикуляр Н – основание перпендикуляра наклонная N – основание наклонной HN – проекция наклонной Расстоянием от точки до прямой является длина перпендикуляра MH < MN
Cлайд 3
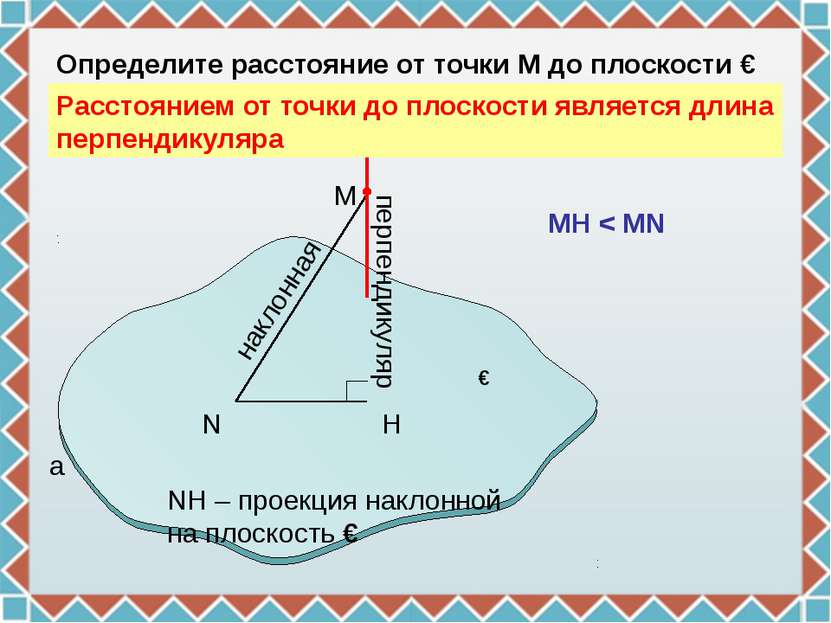
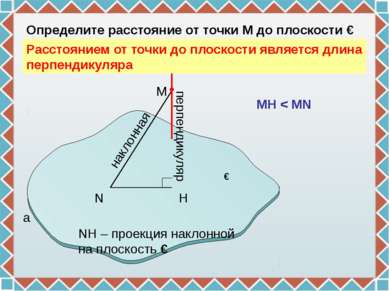N H M a перпендикуляр наклонная Определите расстояние от точки М до плоскости ɣ ɣ NH – проекция наклонной на плоскость ɣ MH < MN Расстоянием от точки до плоскости является длина перпендикуляра
Cлайд 4
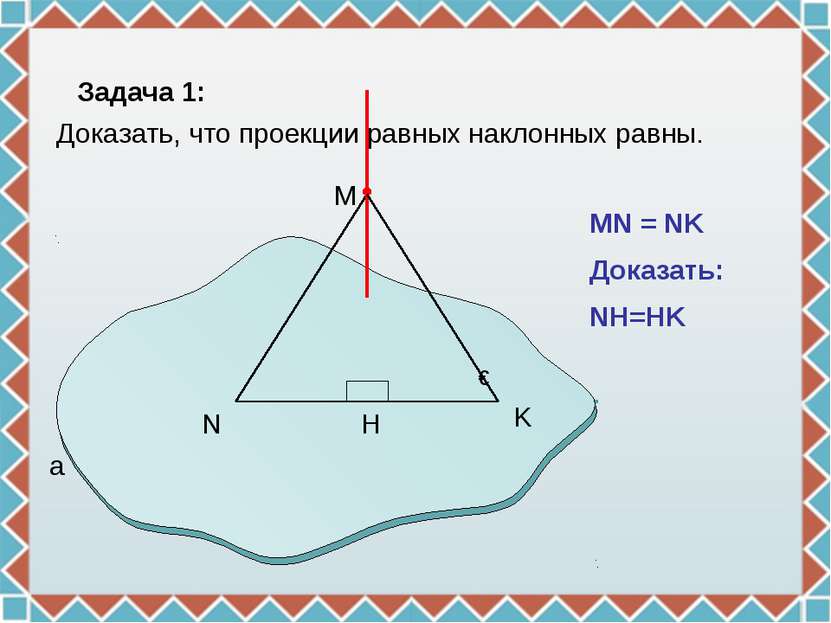
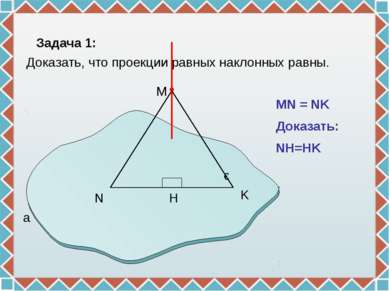N H M a ɣ MN = NK Доказать: NH=HK Задача 1: Доказать, что проекции равных наклонных равны. K
Cлайд 5
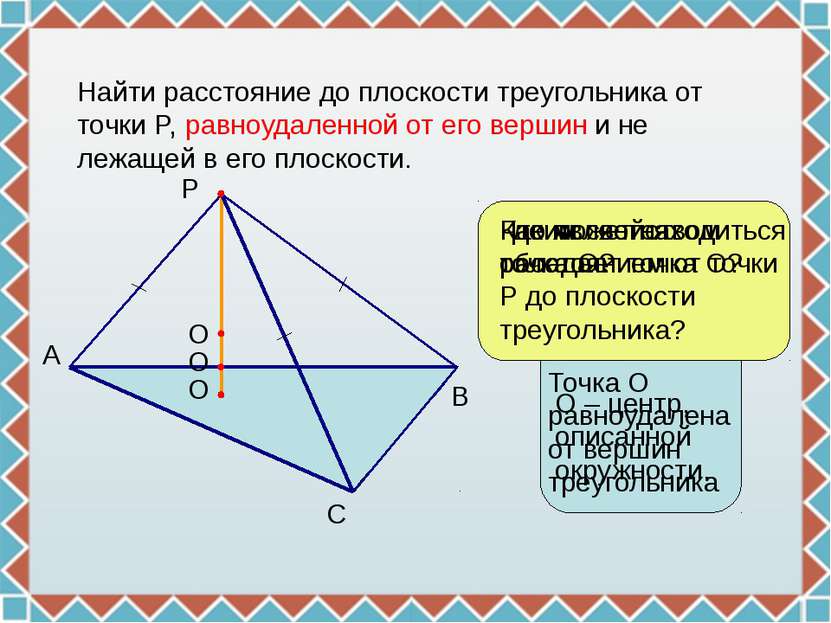
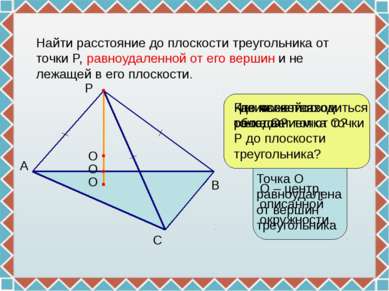Найти расстояние до плоскости треугольника от точки P, равноудаленной от его вершин и не лежащей в его плоскости. P A B C Что является расстоянием от точки Р до плоскости треугольника? О О О Где может находиться точка О? Каким свойством обладает точка О? Точка О равноудалена от вершин треугольника О – центр, описанной окружности.
Cлайд 6
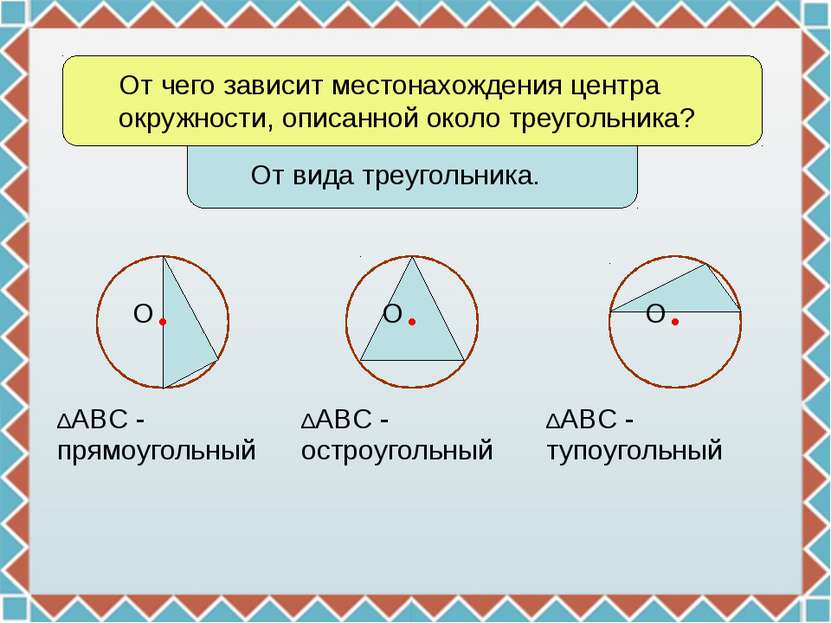
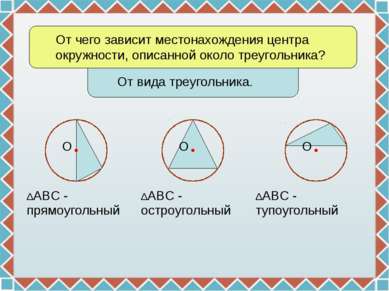От чего зависит местонахождения центра окружности, описанной около треугольника? От вида треугольника. О О О ΔABC -прямоугольный ΔABC -остроугольный ΔABC -тупоугольный
Cлайд 7
План решения задачи: Определить вид треугольника и местонахождение точки О. Найти радиус описанной окружности. ΔАВС 3. По теореме Пифагора найти расстояние РО Прямоугольный R=c/2,где с – гипотенуза треугольника Правильный R= ,где а – сторона треугольника Остроугольный и тупоугольный R= S= Р=(a+b+c)/2
Cлайд 8
Задача 2: Ответ: Ответ: 1 пара:Найти расстояние от точки К до плоскости равностороннего треугольника со стороной 6 см и равноудаленной от его вершин на расстояние равное 8. 2 пара:Точка М находится на расстоянии 15 см от всех вершин треугольника со сторонами 6 см, 10 см, 8 см. Найти расстояние от точки М до плоскости треугольника.
Cлайд 9
Задача 3: Ответ: Ответ: 1 пара:Точка К находится на расстоянии 7 см от вершин треугольника со сторонами 5 см, 5 см, 6 см. Найти расстояние от точки К до плоскости треугольника. 2 пара:Точка К находится на расстоянии 8 см от вершин треугольника со сторонами 5 см, 5 см, 8 см. Найти расстояние от точки К до плоскости треугольника.
