X
Код презентации скопируйте его
Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)
Скачать эту презентацию
Презентация на тему Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)
Скачать эту презентациюCлайд 1
Подготовил: учитель математики МОУ «СОШ №10 с. Солдато-Александровского» Кобзев Д.А. 2012 – 2013 уч.г. (Расстояние от точки до плоскости)
Cлайд 2
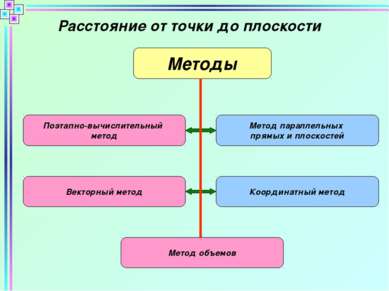Расстояние от точки до плоскости Методы Поэтапно-вычислительный метод Метод параллельных прямых и плоскостей Векторный метод Координатный метод Метод объемов
Cлайд 3
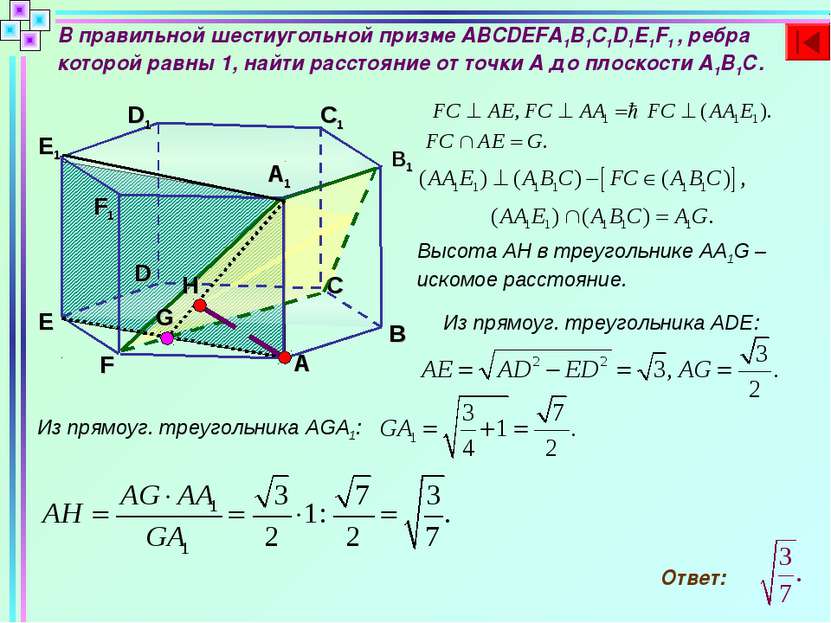
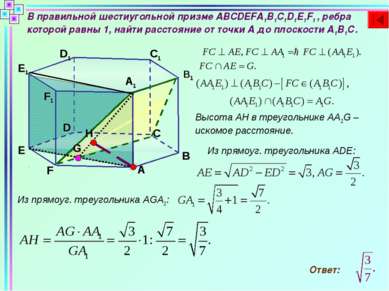В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости А1В1С. B C D A C1 D1 E1 F1 A1 B1 E F G H Высота АН в треугольнике АА1G – искомое расстояние. Из прямоуг. треугольника ADE: Из прямоуг. треугольника AGA1: Ответ:
Cлайд 4
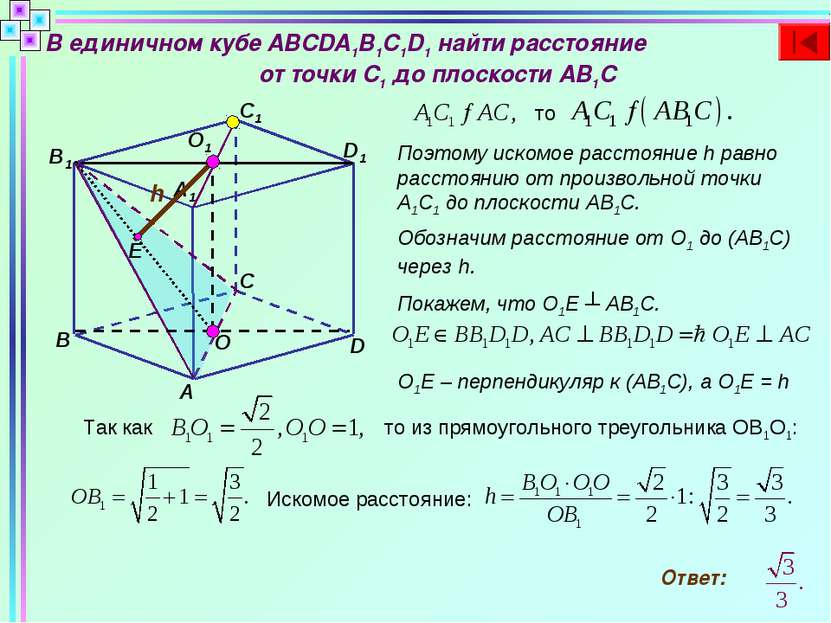
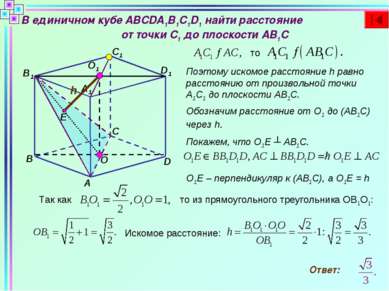В единичном кубе ABCDA1B1C1D1 найти расстояние от точки C1 до плоскости AB1C B D C A A1 B1 C1 D1 то Поэтому искомое расстояние h равно расстоянию от произвольной точки А1С1 до плоскости АВ1С. Е О О1 h Обозначим расстояние от О1 до (АВ1С) через h. Покажем, что О1Е ┴ АВ1С. О1Е – перпендикуляр к (АВ1С), а О1Е = h Так как то из прямоугольного треугольника ОВ1О1: Искомое расстояние: Ответ:
Cлайд 5
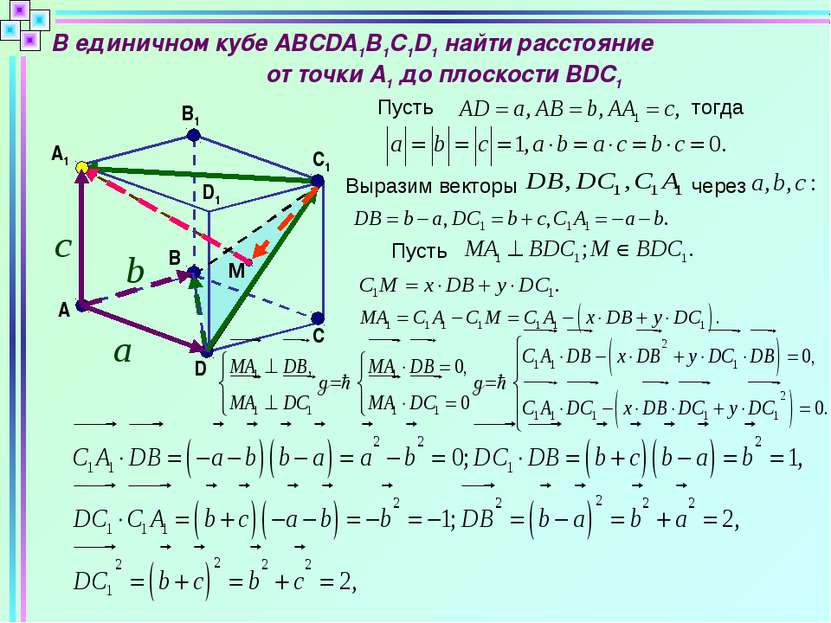
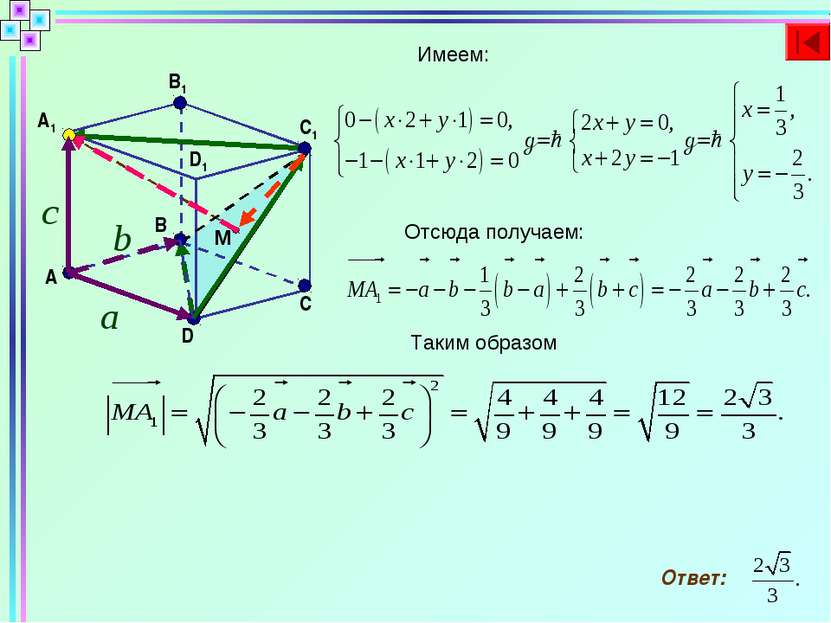
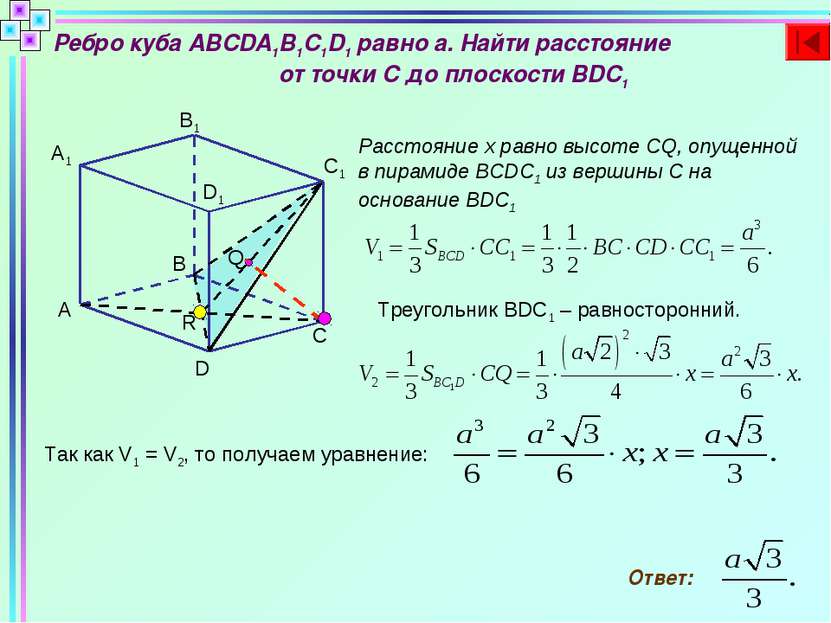
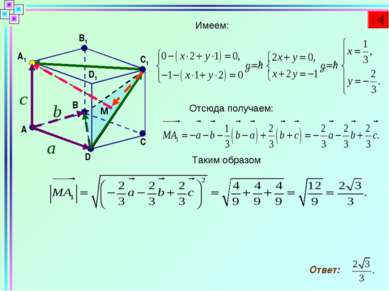
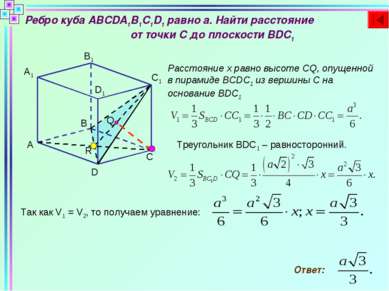
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1 D C B A A1 B1 D1 M C1 Пусть тогда Выразим векторы через Пусть
Cлайд 6
D C B A A1 B1 D1 M C1 Имеем: Отсюда получаем: Таким образом Ответ:
Cлайд 7
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости DEF1 B C D A C1 D1 E1 F1 A1 B1 E F O z y x Введем систему координат и найдем координаты точек: уравнение (DEF1). Подставим координаты точек D, E, F1 в уравнение: уравнение (DEF1): Ответ:
Cлайд 8
Ребро куба ABCDA1B1C1D1 равно а. Найти расстояние от точки C до плоскости BDC1 D C B A A1 B1 C1 D1 Q R Расстояние х равно высоте CQ, опущенной в пирамиде BCDC1 из вершины С на основание BDC1 Треугольник BDC1 – равносторонний. Так как V1 = V2, то получаем уравнение: Ответ:
