X
Код презентации скопируйте его
Теория и методика изучения комплексных чисел в старших классах средней школы
Скачать эту презентацию
Презентация на тему Теория и методика изучения комплексных чисел в старших классах средней школы
Скачать эту презентациюCлайд 1
специальность математика и информатика на тему: «Теория и методика изучения комплексных чисел в старших классах средней школы» Выполнила Юшина Дарья Сергеевна Научный руководитель Латышев Анатолий Васильевич
Cлайд 2
Данная работа состоит из введения, трех глав, заключения и списка используемой литературы. Во введении я отмечаю важность в предоставлении каждому учащемуся возможности достижения определенных целей образования с учетом собственных интересов, способностей и склонностей. Средством реализации чего является дифференциация в обучении. В первой главе рассматриваются психолого-педагогические аспекты учебной деятельности старших школьников и методические основы введения комплексных чисел в старших классах средней школы. Во второй главе приводятся сведения исторического характера о развитии и построении поля комплексных чисел. Третья глава посвящена непосредственно изложению теории комплексных чисел в старших классах средней школы.
Cлайд 3
Современная трактовка дифференциации обучения математике затрагивает два аспекта обучения: процессуальный и содержательный. Этим диктуется необходимость рассматривать два вида дифференциации: Уровневая дифференциация; Дифференциация по содержанию или профильная. Оба вида дифференциации - уровневая и профильная - сосуществуют и взаимно дополняют друг друга на различных ступенях школьного математического образования, однако в разном удельном весе. Развитие среднего общего образования требует значительного улучшения и совершенствования преподавания всех дисциплин. Их содержание должно соответствовать современному уровню науки и техники и в значительной степени определять уровень профессиональной подготовки будущих выпускников средних общеобразовательных школ.
Cлайд 4
Особенности мышления старшеклассников – Мышление становится более глубоким, полным, разносторонним и всё более абстрактным. Мыслительная деятельность отличается у них высоким уровнем обобщения и абстракции, учащиеся стремятся к установлению причинно-следственных связей и других закономерностей между явлениями окружающего мира. Учебная деятельность старшеклассников – Углубляется содержание обучения и вводятся новые учебные разделы, также учебная деятельность старшеклассников предъявляет гораздо более высокие требования к их активности и самостоятельности.
Cлайд 5
Рассмотрим пример дифференцированного изучения темы "Комплексные числа". Эта тема выбрана не случайно: без нее курс школьной математики нельзя считать завершенным, так как в результате введения данного понятия (мнимая единица, комплексное число) получается необходимое расширение множества действительных чисел и поэтому знакомство с комплексными числами должно входить в программу курса математики средних общеобразовательных школ любого профиля, а не только школ с углубленным изучением математики.
Cлайд 6
Истории комплексных чисел посвящено много работ, из которых видно, что появление мнимых чисел относится к ХVI в., а может быть, к еще более раннему времени. В трудах Кардано, Бомбелли, Жираро, Декарта и других математиков они стали называться «величинами», но с обязательным прибавлением эпитетов: «невозможные», «софистические», «мнимые» и т.п. Джеронимо Кардано (1501-1576гг.) решает задачу - нарезать участок земли прямоугольной формы с площадью S=40 (кв.ед.) и периметром 2р=20 (лин.ед). Выражения вида а+√-b появились в книге Кардано «Великое искусство, или о правилах алгебры», вышедшей в 1545г., при решении кубического уравнения х3+px=q: именно потребность решать уравнения второй и третьей степени привела к необходимости строить новую теорию -комплексных чисел. Первые правила арифметических действий над такими числами были введены итальянским алгебраистом Бомбелли в 1572 году.
Cлайд 7
В работе «Введение в математический анализ» (1746г.) Леонардо Эйлер, приняв название мнимой единицы Р.Декарда imaginaires, вводит первую букву этого слова i для обозначения , так что i2=-1, и вводит функцию еxi . Позднее, в 1831г. Гаусс предложил геометрическую интерпретацию комплексных чисел, которая позволила дать обоснование многим понятиям теории комплексных чисел. Геометрическое истолкование комплексных чисел независимо от Гаусса и друг от друга было получено также датчанином Весселем (1797г.) и французом Арганом (1806г.) Так, Софья Ковалевская (1850-1891) решила, используя теорию функций комплексного переменного, задачу о вращении твердого тела вокруг неподвижной точки, решение которой в течение долгого времени не поддавалось усилиям многих математиков и механиков. Н.Е. Жуковский при помощи функции , которая в настоящее время носит его имя, вывел формулу для определения подъемной силы крыла.
Cлайд 8
«Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что сочетание бытия с небытием» Г. Лейбниц
Cлайд 9
Представление о числе изменялось по мере расширения круга задач.
Cлайд 10
Понятие комплексного числа Название «комплексные» происходит от слова «составные» — по виду выражения a+bi. Равенство комплексных чисел Два комплексных числа a+bi и c+di называются равными тогда и только тогда, когда а=с и b=d, т. е. когда равны их действительные и мнимые части. Например, 1,5+√9i=3/2+3i, т.к. 1,5=3/2 и √9=3 Сложение и умножение комплексных чисел (a+bi)+(c+di)=(a+c)+(b+d)i. (a+bi)(с+di)=(ас-bd)+(ad+bc)i. Комплексно сопряженные числа Сопряженным с числом z=a+bi называется комплексное число a-bi
Cлайд 11
Модуль комплексного числа Модулем комплексного числа z=a+bi называется число Вычитание комплексных чисел Если z1=a1+b1i, z2 =a2+b2i, то разность z1-z2 имеет следующий вид: (а1+b1i)-(а2+b2i)=(a1-а2)+(b1-b2)i. Деление комплексных чисел
Cлайд 12
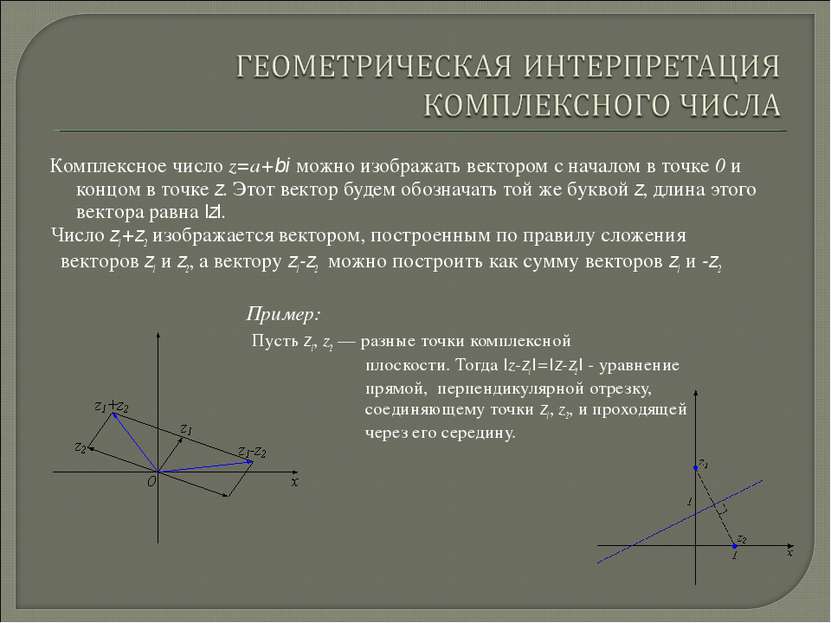
Комплексное число z=а+bi можно изображать вектором с началом в точке 0 и концом в точке z. Этот вектор будем обозначать той же буквой z, длина этого вектора равна |z|. Число z1+z2 изображается вектором, построенным по правилу сложения векторов z1 и z2, а вектору z1-z2 можно построить как сумму векторов z1 и -z2 Пример: Пусть z1, z2 — разные точки комплексной плоскости. Тогда |z-z1|=|z-z2| - уравнение прямой, перпендикулярной отрезку, соединяющему точки z1, z2, и проходящей через его середину.
Cлайд 13
Любое комплексное число z=a+bi, где z≠0, представляется в виде z=r(cosφ +i sinφ ) С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел zl и z2. z1z2=r1r2(cos( φ1+ φ2)+i sin( φ1+ φ2)). Вообще для любого n из N (и для всех n из Z) справедлива формула (cosφ +i sinφ )n=cos φn +i sin φn, которую называют формулой Муавра. Для n-й степени комплексного числа, записанного в тригонометрической форме z=r(cosφ +i sin φ), справедлива формула zn=rn(cos φn +i sin φn ).
Cлайд 14
Рассмотрим уравнение z2=a, где а — заданное действительное число, z — неизвестное. Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами az2+bz+c=0 по известной общей формуле. Пример: Решить уравнение z2-16z+65=0. По общей формуле находим т. е. z1=8+i, z2=8-i.
Cлайд 15
Число z называется корнем степени n из числа w (обозначается ), если zn=w. Все решения уравнения zn=w могут быть записаны следующим образом: k=0, 1, 2, …, n-1.
Cлайд 16
Положим по определению eiφ=cosφ+isinφ называется формулой Эйлера. Тогда любое комплексное число z≠0 можно записать в виде: z=r(cosφ+isinφ)=reiφ Эта форма записи комплексного числа называется показательной.
