X
Код презентации скопируйте его
Геометрические построения на плоскости
Скачать эту презентациюПрезентация на тему Геометрические построения на плоскости
Скачать эту презентациюCлайд 2
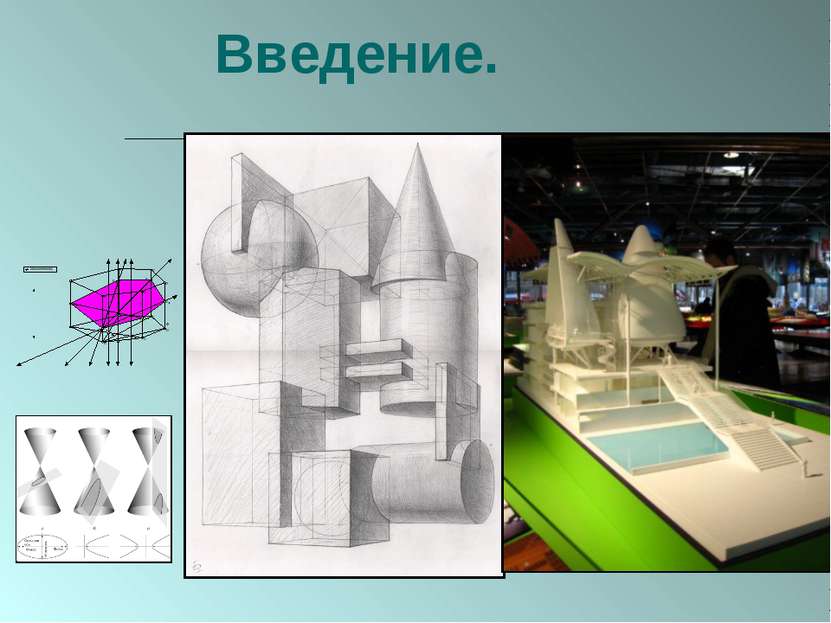
 Цель: Исследование роли «геометрического построения на плоскости» в геометрии и архитектуре. Задачи: 1.Изучить научную литературу, ресурсы сети Интернет по исследуемой теме. 2.Выявить роль задач на построение сечений в геометрии, архитектуре. 3.Показать: а) непосредственную связь геометрии и архитектуры. б) прикладные возможности задач на построение сечений. в) значимость задач в развитии современной науки.
Цель: Исследование роли «геометрического построения на плоскости» в геометрии и архитектуре. Задачи: 1.Изучить научную литературу, ресурсы сети Интернет по исследуемой теме. 2.Выявить роль задач на построение сечений в геометрии, архитектуре. 3.Показать: а) непосредственную связь геометрии и архитектуры. б) прикладные возможности задач на построение сечений. в) значимость задач в развитии современной науки.
Cлайд 3
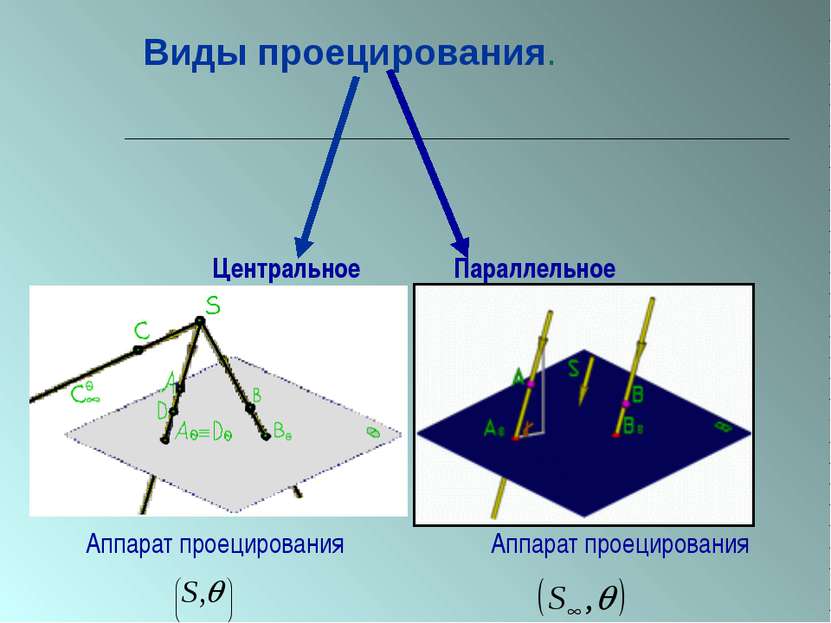
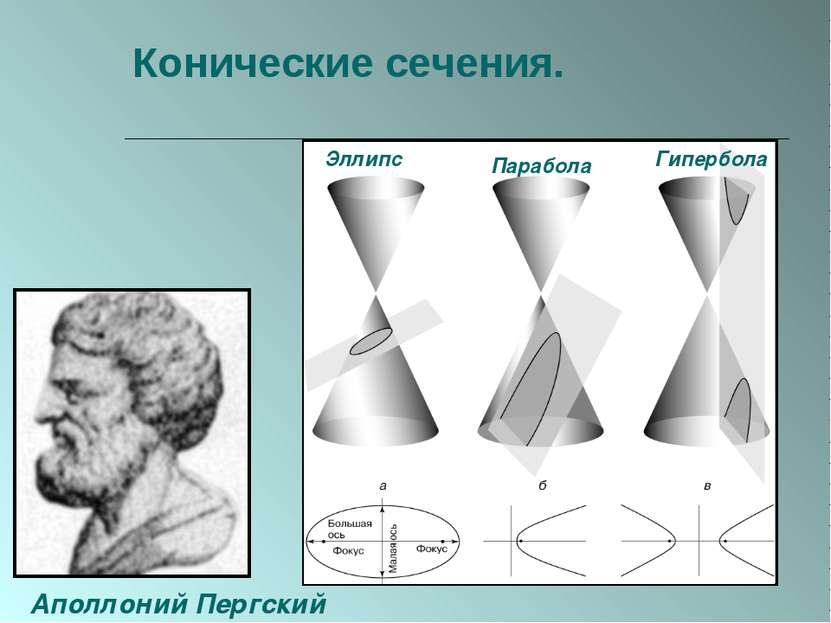
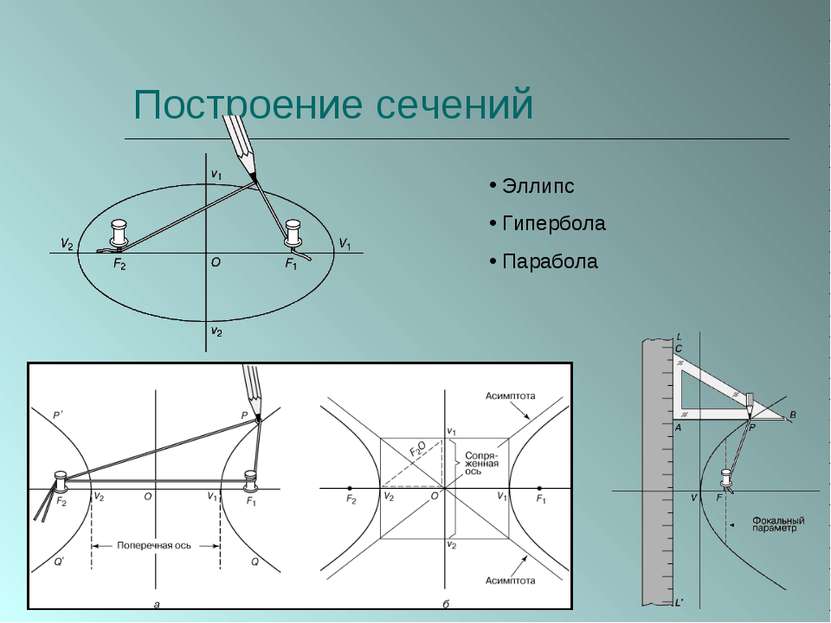
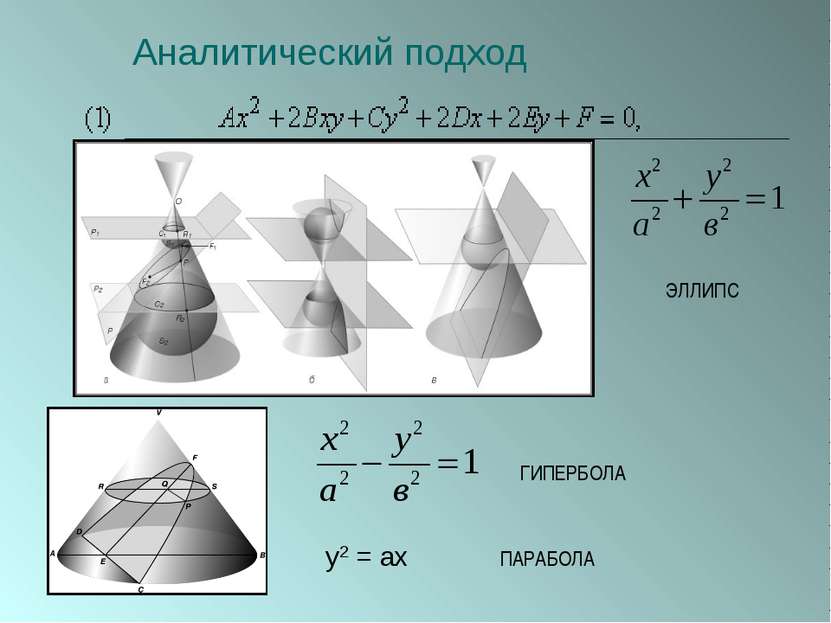
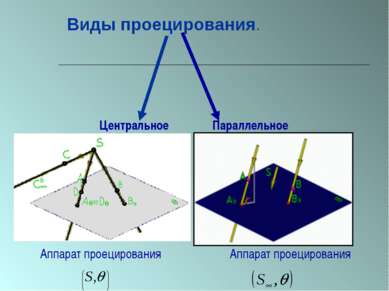
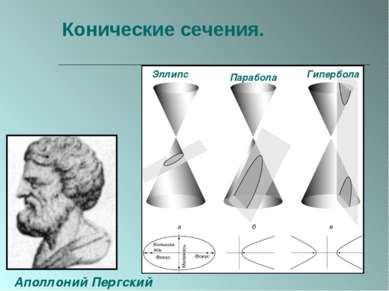
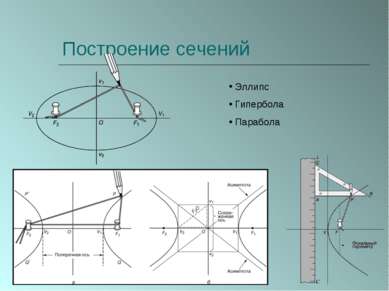
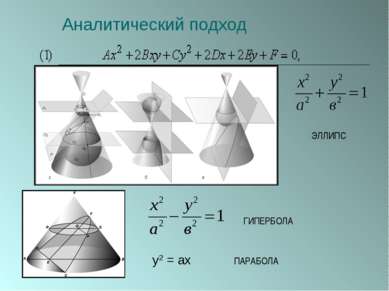
 ПЛАН 1. Введение. 2. Из истории начертательной геометрии. 3. Виды проецирования. 1) центральное проецирование; 2) параллельное проецирование; 3) основные независимые свойства параллельного проецирования. 4. Пересечение многогранников плоскостью. 1) методы построения сечений многогранников: - метод следов; - решение задач на построение сечений многогранников; - способ внутреннего проектирования; - решение задач на построение сечений многогранников. 5. Конические сечения. 1) ранняя история; 2) построение конических сечений: - эллипс; - гипербола; - парабола. 3) свойства конических сечений: - определения Папа; - конструкция Данделена; - другие свойства. 4) аналитический подход: - алгебраическая классификация; - вывод уравнений конических сечений. 5) проективный подход; 6) специальные построения; 6. Заключение. 7. Список используемой литературы
ПЛАН 1. Введение. 2. Из истории начертательной геометрии. 3. Виды проецирования. 1) центральное проецирование; 2) параллельное проецирование; 3) основные независимые свойства параллельного проецирования. 4. Пересечение многогранников плоскостью. 1) методы построения сечений многогранников: - метод следов; - решение задач на построение сечений многогранников; - способ внутреннего проектирования; - решение задач на построение сечений многогранников. 5. Конические сечения. 1) ранняя история; 2) построение конических сечений: - эллипс; - гипербола; - парабола. 3) свойства конических сечений: - определения Папа; - конструкция Данделена; - другие свойства. 4) аналитический подход: - алгебраическая классификация; - вывод уравнений конических сечений. 5) проективный подход; 6) специальные построения; 6. Заключение. 7. Список используемой литературы
Cлайд 7
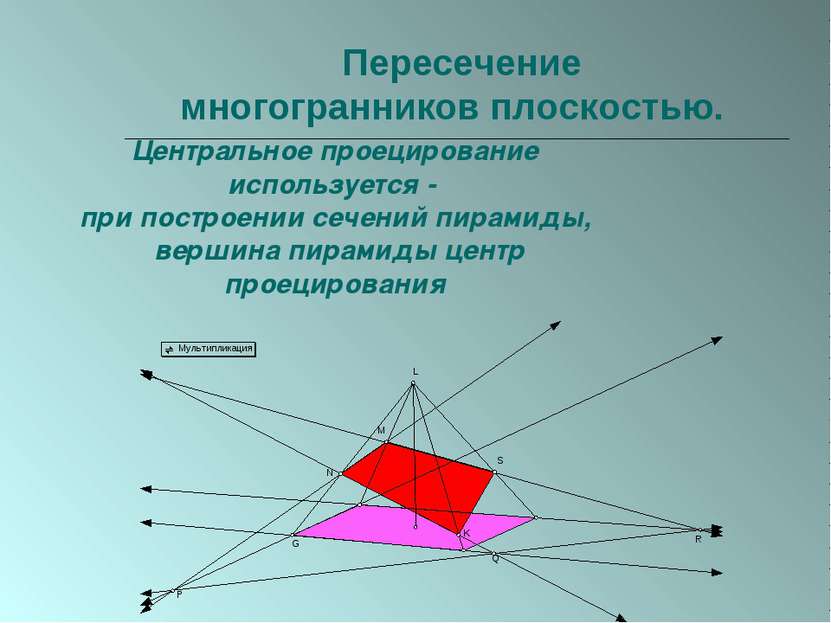
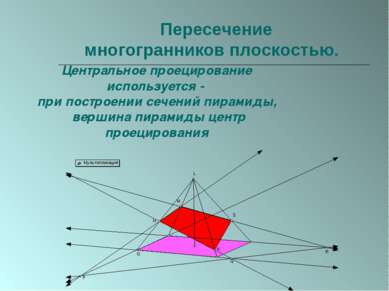 Пересечение многогранников плоскостью. Центральное проецирование используется - при построении сечений пирамиды, вершина пирамиды центр проецирования
Пересечение многогранников плоскостью. Центральное проецирование используется - при построении сечений пирамиды, вершина пирамиды центр проецирования
Cлайд 8
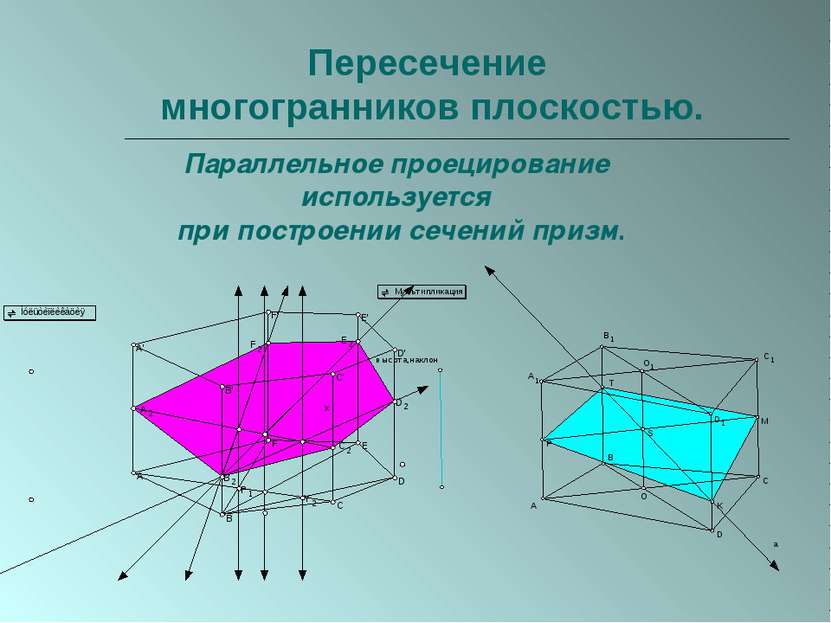
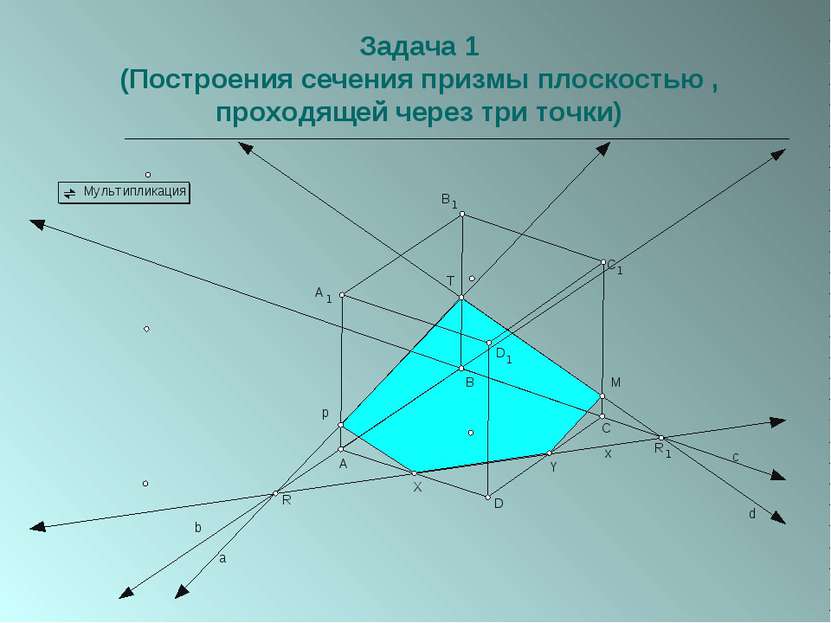
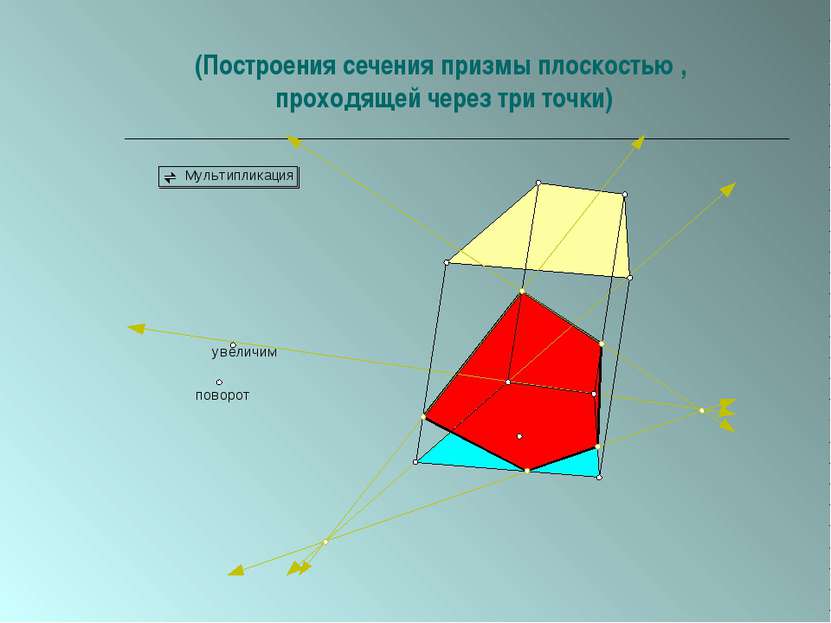
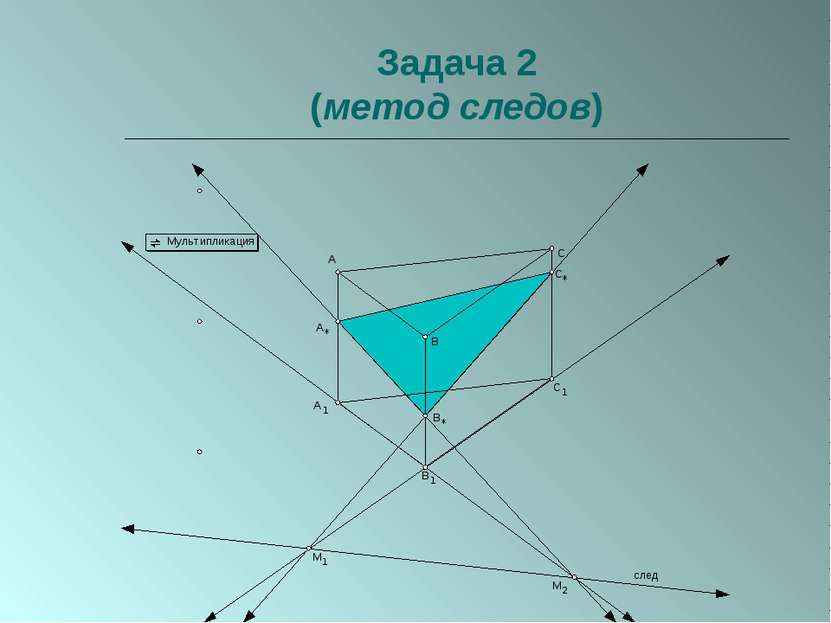
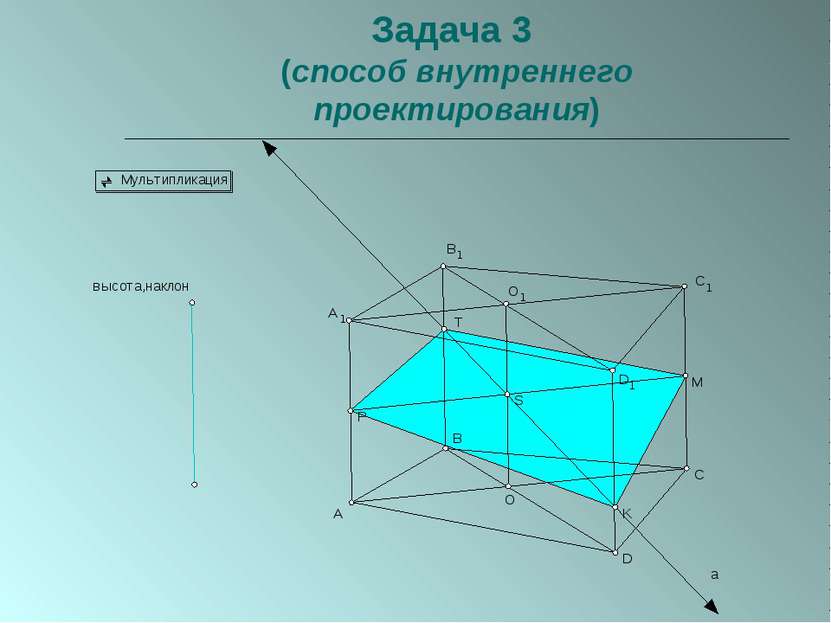
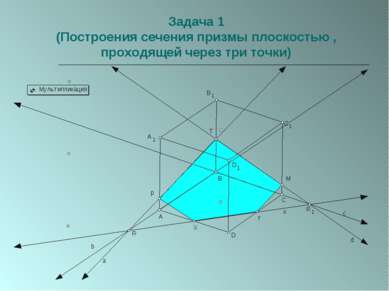
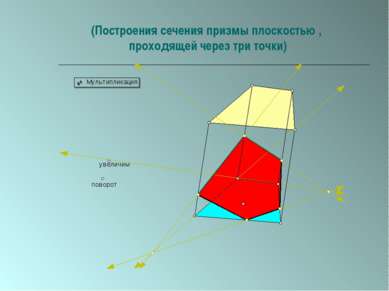
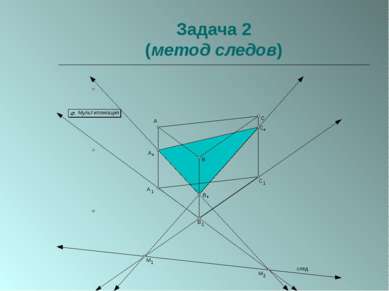
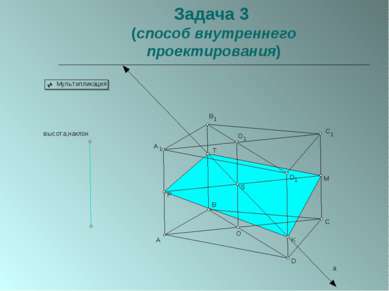
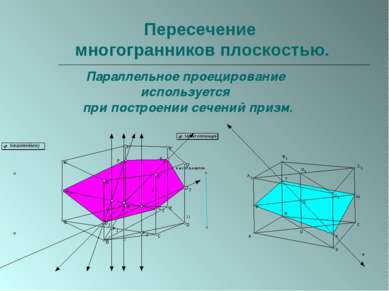 Пересечение многогранников плоскостью. Параллельное проецирование используется при построении сечений призм.
Пересечение многогранников плоскостью. Параллельное проецирование используется при построении сечений призм.