X
Код презентации скопируйте его
Движение тел по наклонной плоскости
Скачать эту презентацию
Презентация на тему Движение тел по наклонной плоскости
Скачать эту презентациюCлайд 1
Cлайд 2
Алгоритм решения задач на законы динамики: Записать условие задачи, перевести данные в СИ; Сделать чертёж, на котором указать все силы, действующие на тело, вектор ускорения, направление координатных осей; Записать 2 закон Ньютона векторной форме, где F- равнодействующая всех сил, действующих на тело; Определить знаки проекций сил на координатные оси и переписать 2 закон Ньютона с учётом этих знаков; Решить полученное уравнение (систему уравнений) относительно неизвестной величины.
Cлайд 3
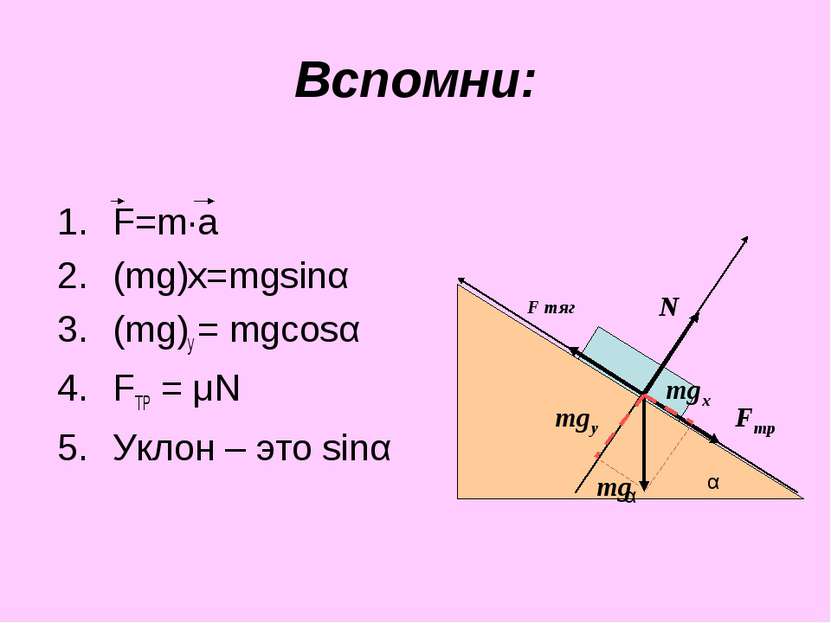
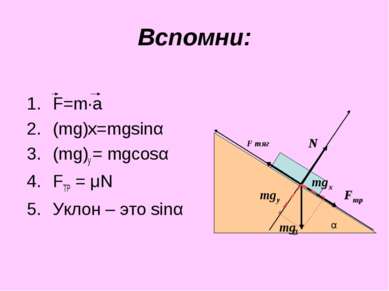Вспомни: F=m·a (mg)х=mgsinα (mg)у = mgcosα FТР = μN Уклон – это sinα mg N Fтр F тяг mgх mgу α α
Cлайд 4
Выполните следующие задания: По данным составьте задачу; Опишите движение; Запишите второй закон Ньютона в векторной форме; Запишите второй закон Ньютона в скалярной форме Выразите действующую силу тяги; Найдите ускорение, с которым движется тело.
Cлайд 5
μ =0 a> 0 a v Тело движется вверх по наклонной плоскости N F mg a= F=m·( g· sinα+a) α
Cлайд 6
μ =0 a< 0 a v Тело движется вверх по наклонной плоскости N F mg a= F=m·( g· sinα-a) α
Cлайд 7
μ =0 a= 0 v Тело движется вверх по наклонной плоскости N F mg F=mg· sinα α
Cлайд 8
μ =0 a> 0 Тело движется вниз по наклонной плоскости N F mg a= F=m·( a - g·sinα) α a V
Cлайд 9
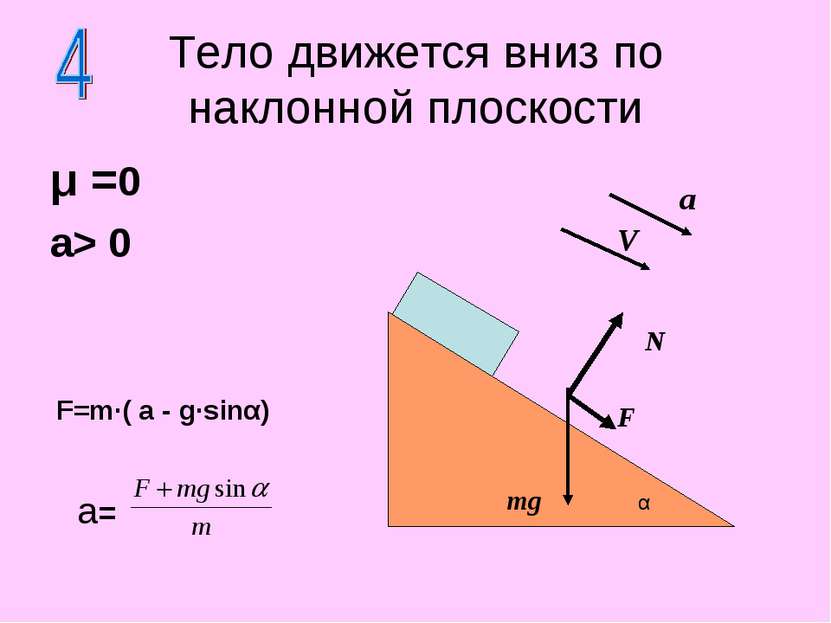
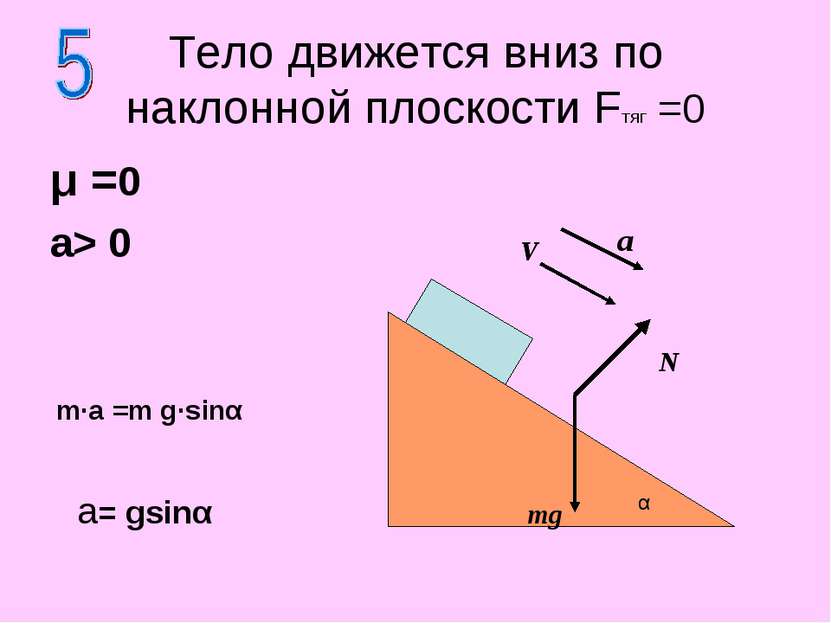
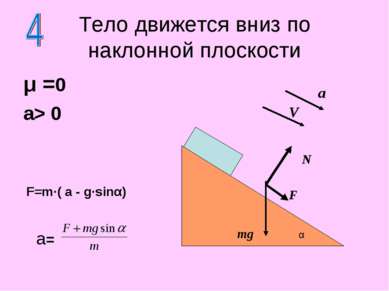
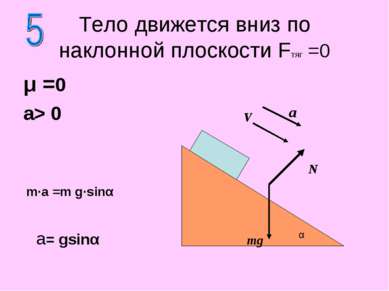μ =0 a> 0 Тело движется вниз по наклонной плоскости Fтяг =0 N mg a= gsinα m·a =m g·sinα α a V V
Cлайд 10
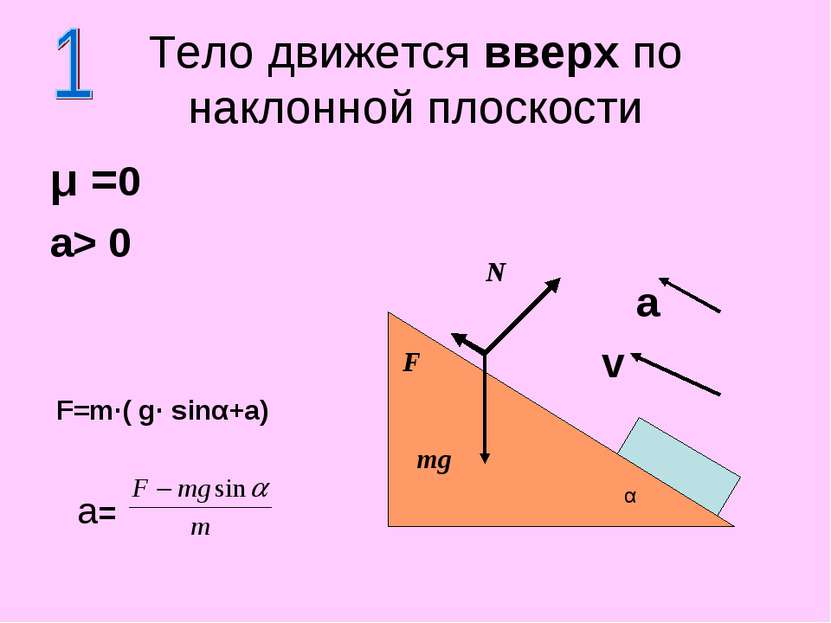
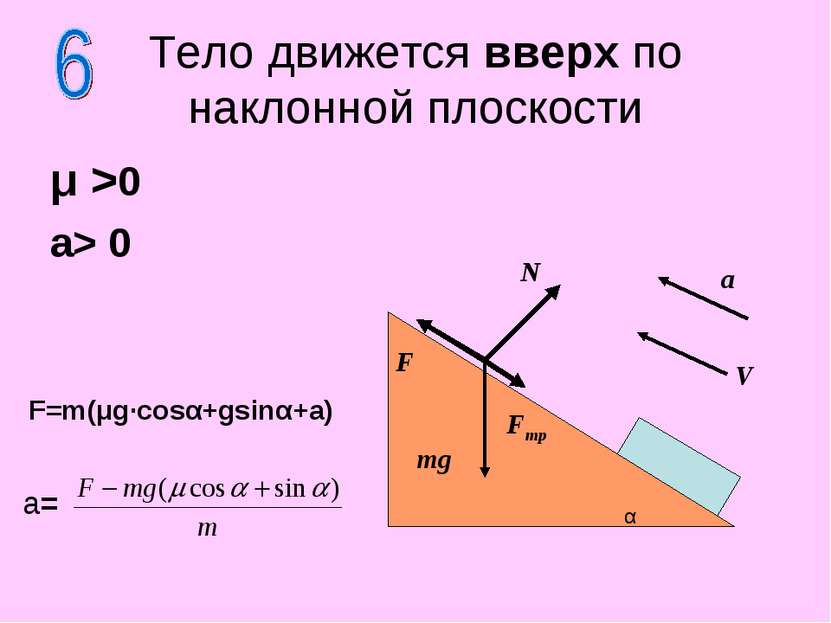
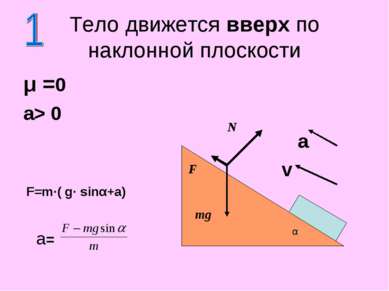
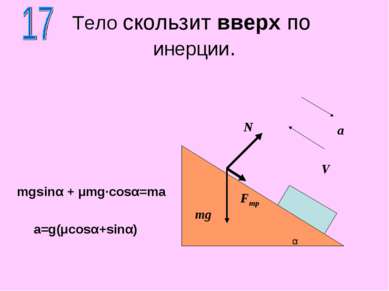
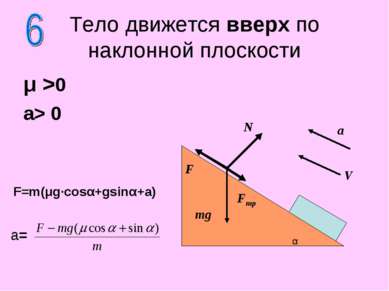μ >0 a> 0 Тело движется вверх по наклонной плоскости N F mg F=m(μg·cosα+gsinα+a) α Fтр V a a=
Cлайд 11
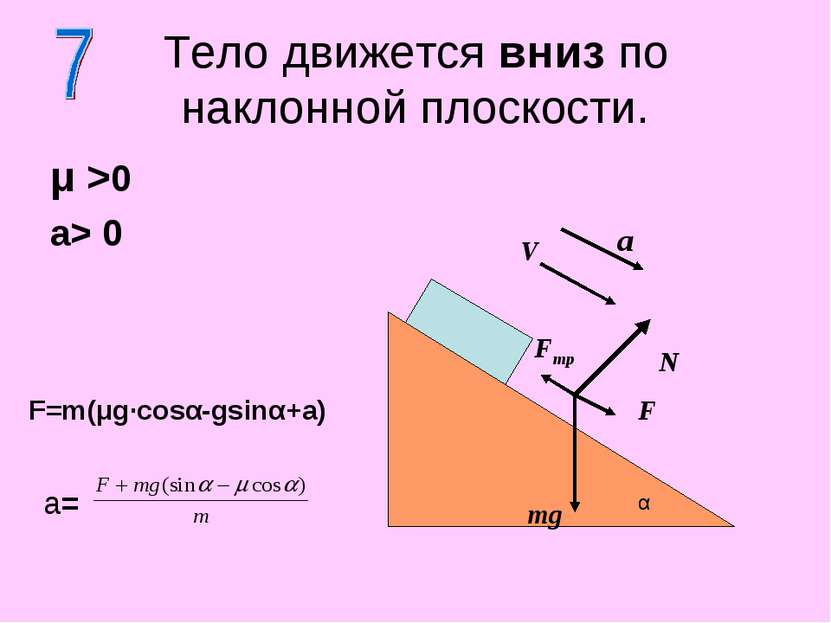
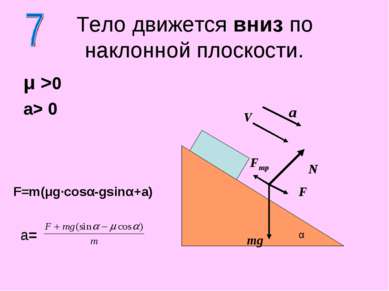Тело движется вниз по наклонной плоскости. μ >0 a> 0 N mg α a V F Fтр F=m(μg·cosα-gsinα+a) a=
Cлайд 12
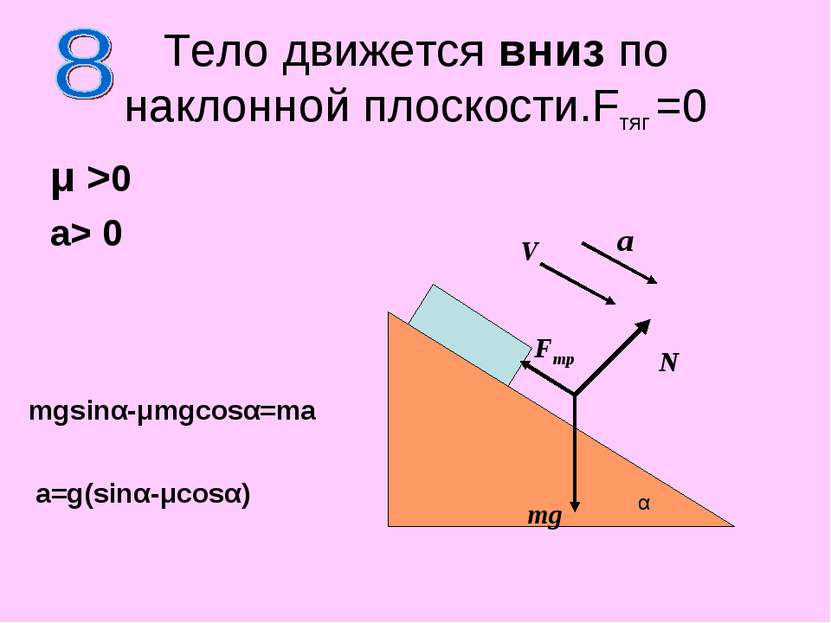
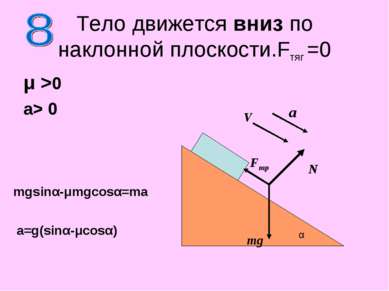Тело движется вниз по наклонной плоскости.Fтяг =0 μ >0 a> 0 N mg α a V Fтр mgsinα-μmgcosα=ma a=g(sinα-μcosα)
Cлайд 13
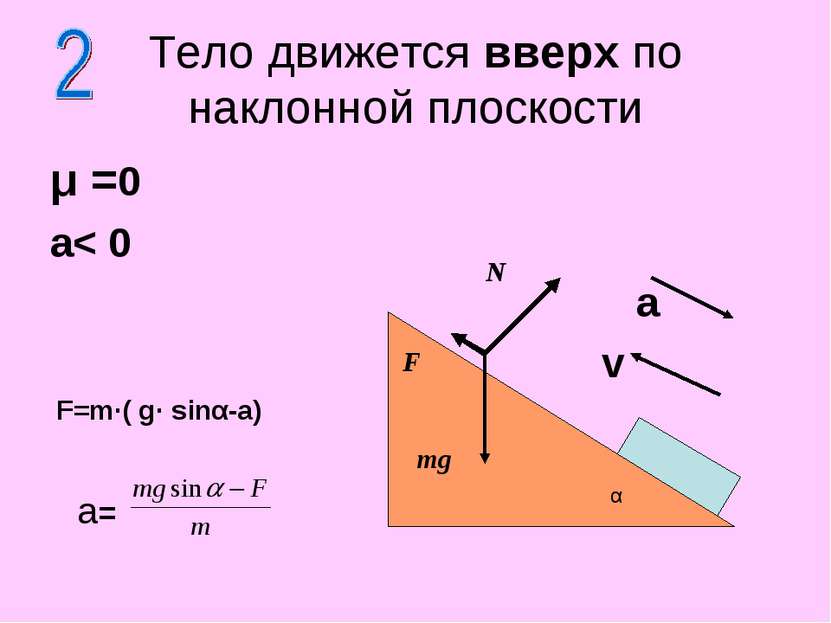
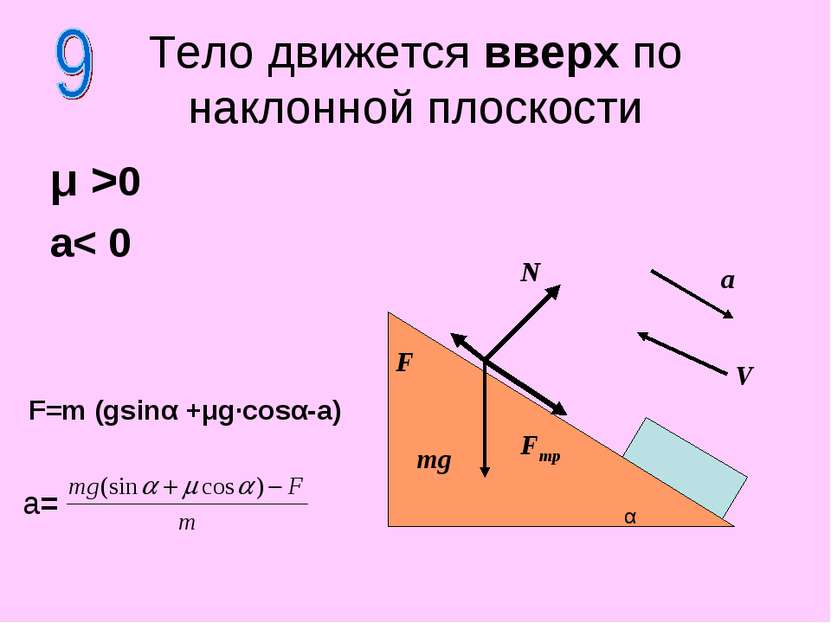
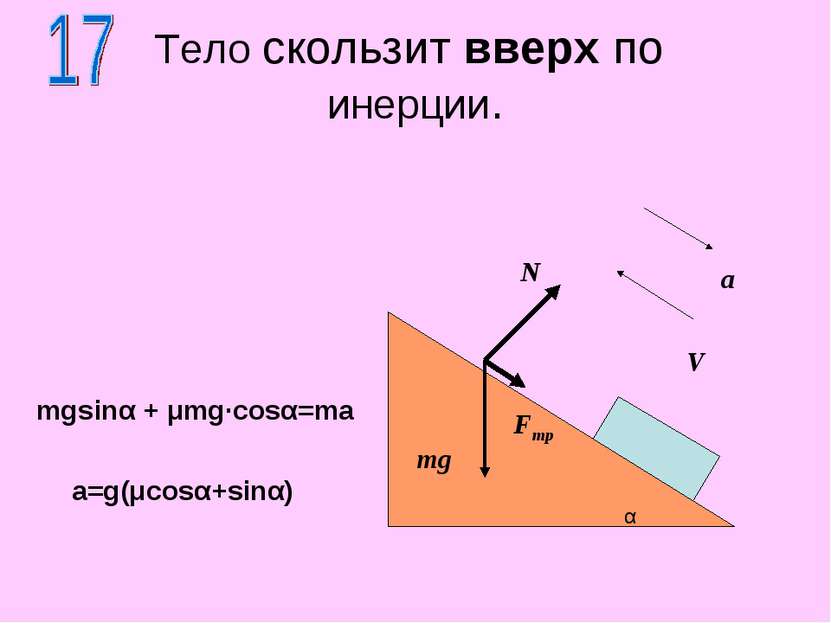
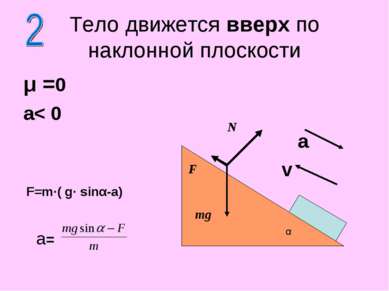
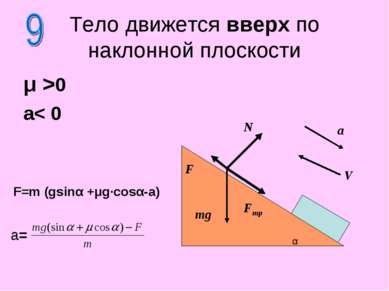μ >0 a< 0 Тело движется вверх по наклонной плоскости N F mg F=m (gsinα +μg·cosα-a) α Fтр V a a=
Cлайд 14
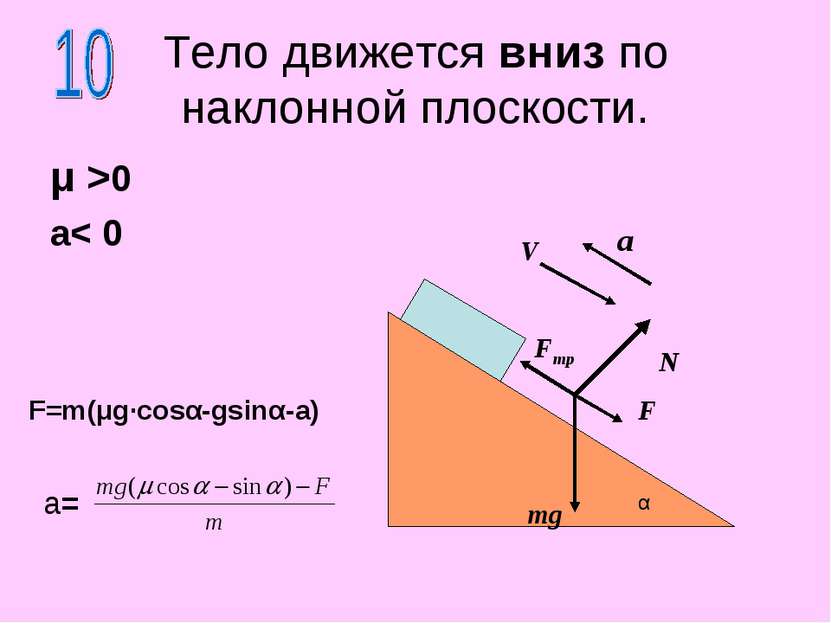
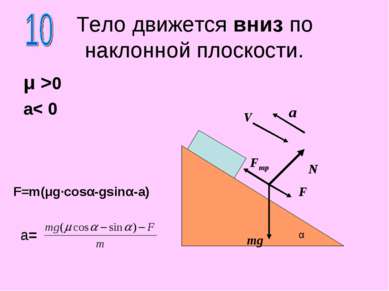Тело движется вниз по наклонной плоскости. μ >0 a< 0 N mg α a V F Fтр F=m(μg·cosα-gsinα-a) a=
Cлайд 15
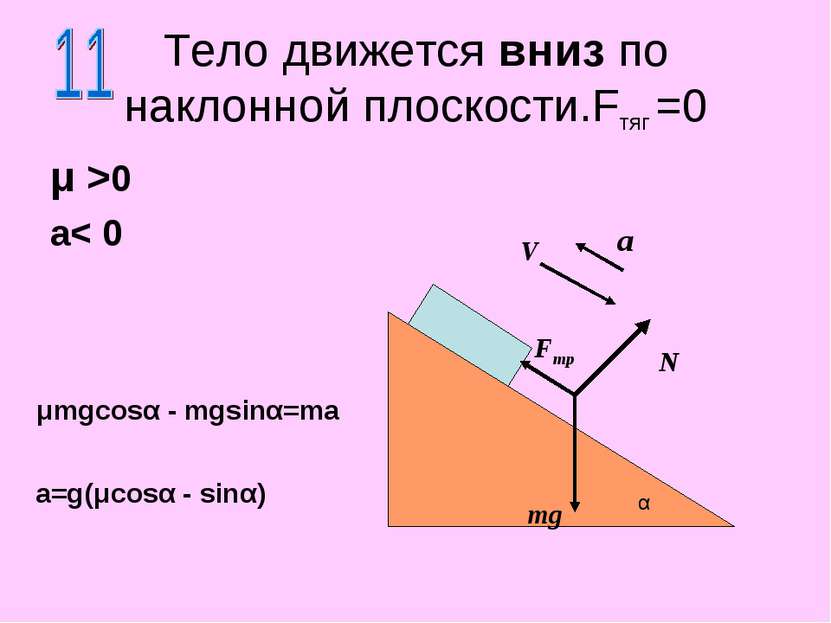
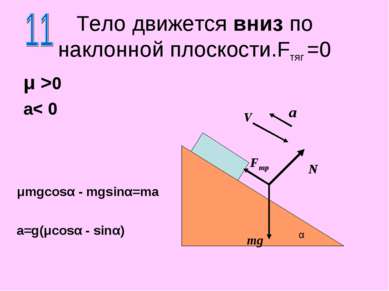Тело движется вниз по наклонной плоскости.Fтяг =0 μ >0 a< 0 N mg α a V Fтр μmgcosα - mgsinα=ma a=g(μcosα - sinα)
Cлайд 16
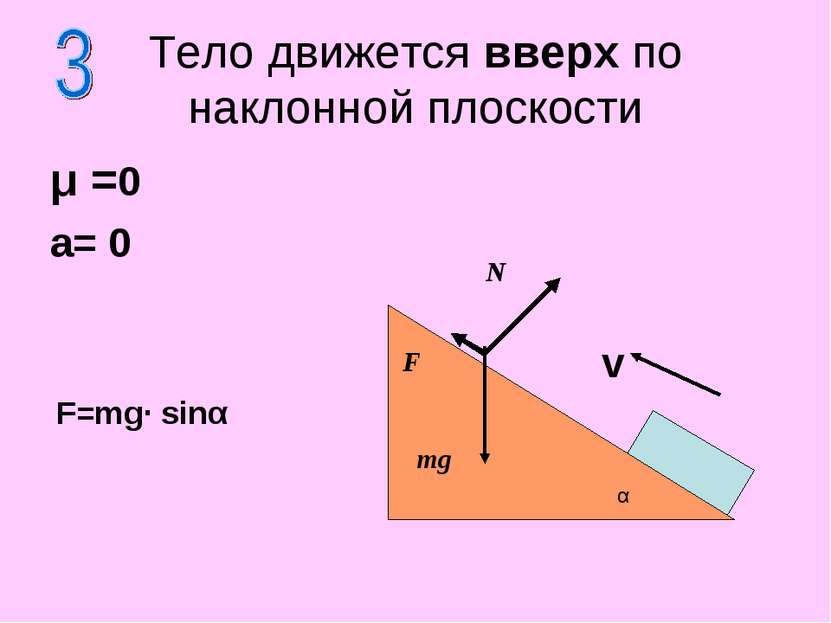
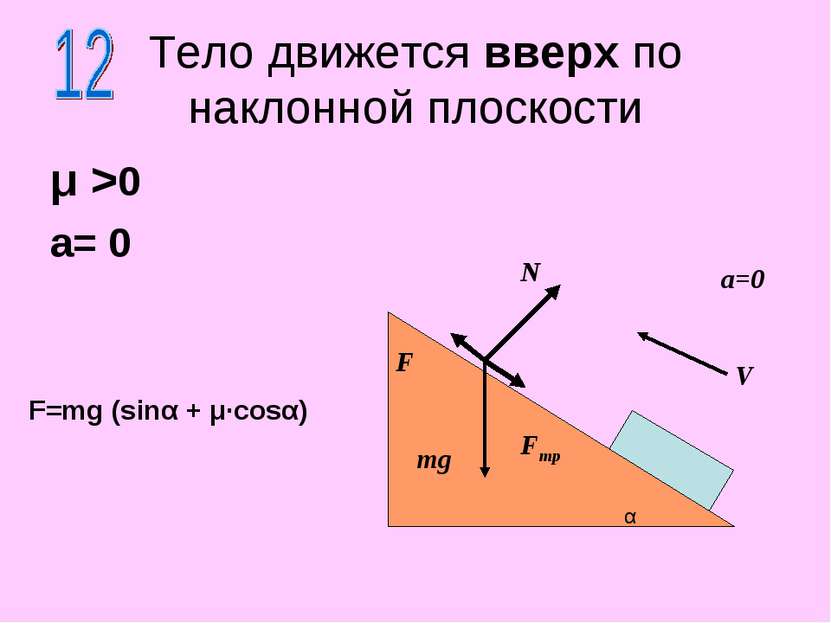
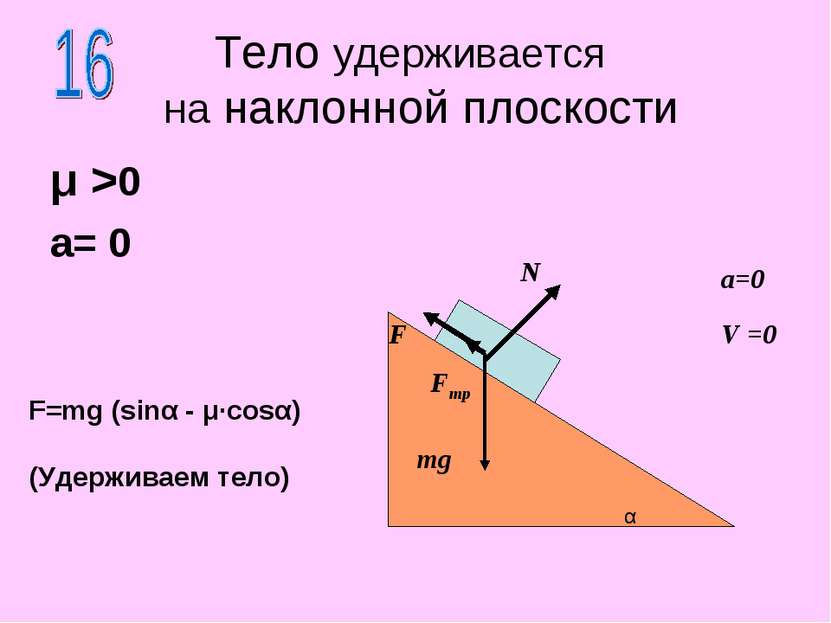
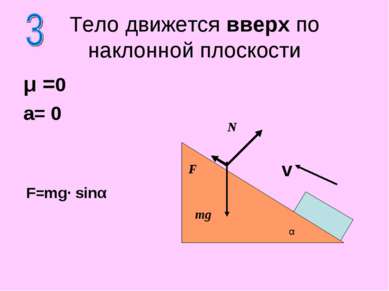
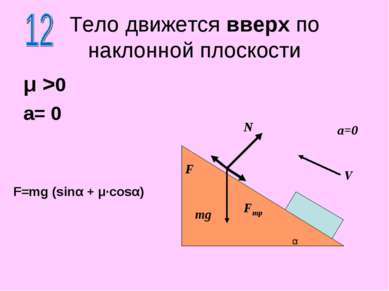μ >0 a= 0 Тело движется вверх по наклонной плоскости N F mg F=mg (sinα + μ·cosα) α Fтр V a=0
Cлайд 17
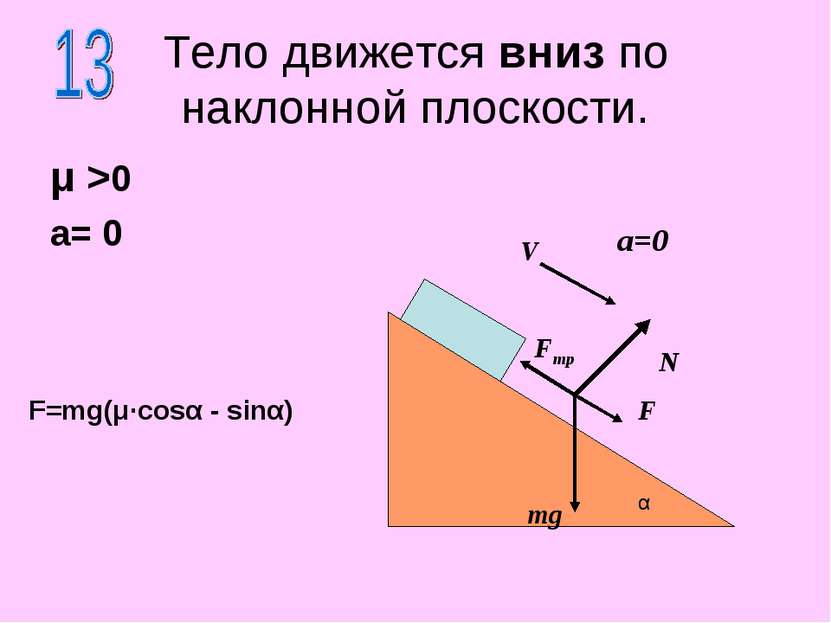
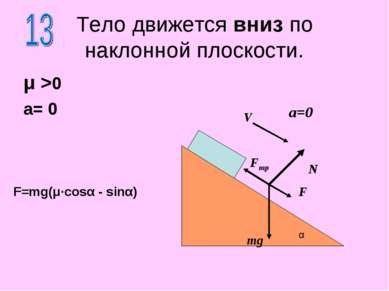Тело движется вниз по наклонной плоскости. μ >0 a= 0 N mg α a=0 V F Fтр F=mg(μ·cosα - sinα)
Cлайд 18
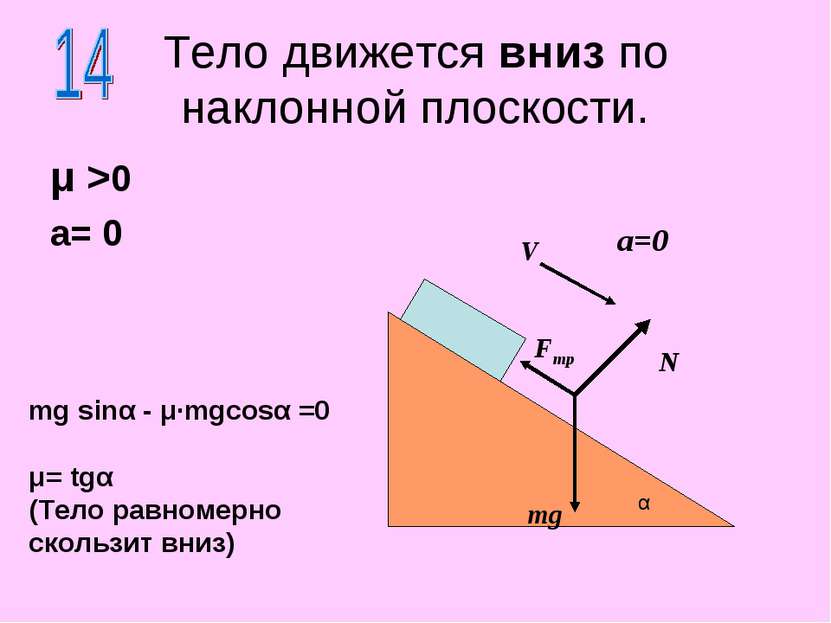
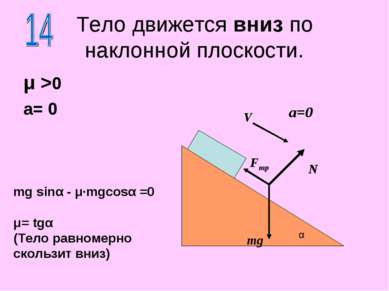Тело движется вниз по наклонной плоскости. μ >0 a= 0 N mg α a=0 V Fтр mg sinα - μ·mgcosα =0 μ= tgα (Тело равномерно скользит вниз)
Cлайд 19
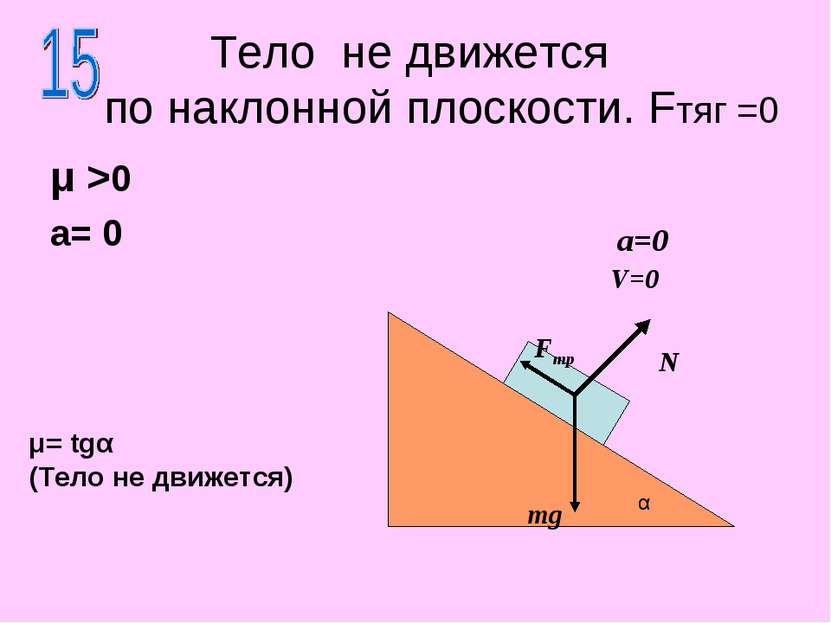
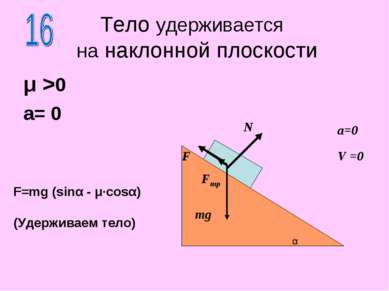
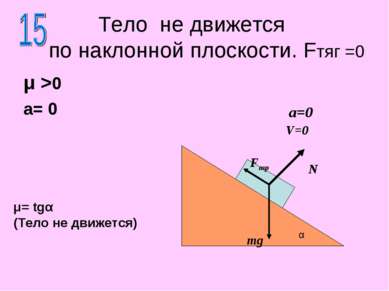Тело не движется по наклонной плоскости. Fтяг =0 μ >0 a= 0 N mg α a=0 V=0 Fтр μ= tgα (Тело не движется)
Cлайд 20
μ >0 a= 0 Тело удерживается на наклонной плоскости N F mg F=mg (sinα - μ·cosα) (Удерживаем тело) α Fтр V =0 a=0
Cлайд 21
Тело скользит вверх по инерции. N mg mgsinα + μmg·cosα=ma α Fтр V a a=g(μcosα+sinα)
Cлайд 22
Карта задач μ=0 μ>0 вверх вниз Fтяг=0 вверх вниз Fтяг=0 a>0 №1 №4 №5 №6 №7 №8 a
