X
Код презентации скопируйте его
Задачи на движение по замкнутой линии
Скачать эту презентацию
Презентация на тему Задачи на движение по замкнутой линии
Скачать эту презентациюCлайд 1
Задачи на движение по замкнутой линии Выполнили: Кузнецов Алексей, Быкова Наталья, ученики 10 класса Руководители: Соколова В.А., учитель математики, Попова И.А., учитель физики Городской конкурс Научно-Исследовательских работ учащихся «Первые шаги» Белово 2011
Cлайд 2
Актуальность: Задание В12 из ЕГЭ включает в себя практически все типы текстовых задач, среди них - задания на движение по окружности; В литературе отсутствуют универсальные рекомендации к решению задач на движение по окружности
Cлайд 3
Новизна: обобщение полученных знаний и опыта в решении задач на движение по окружности с учетом математических и физических методов, терминологии и формул; составление алгоритма решения для основных сюжетных вариантов.
Cлайд 4
Цель: оптимизация процесса решения текстовых задач на движение по замкнутой линии на основе сопоставления различных подходов и методов решения
Cлайд 5
Задачи: Исследовать большое количество текстовых задач на движение по замкнутой линии из материалов ЕГЭ, олимпиад различного уровня; Исследовать задачи на движение по окружности из курса физики; Сопоставить математические и физические методы решения задач, выявить аналогию решения; Составить алгоритм решения для решения текстовых задач на движение по замкнутой линии.
Cлайд 6
Некоторые задачи из курса математики Задача 1. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. В задаче используются величины, связанные с расстоянием; с точки зрения физики – линейные величины (линейная скорость, длина окружности) v t s велосипедист x мотоциклист y
Cлайд 7
Некоторые задачи из курса математики и физики Задача 2. Через какое время, начиная с 8.00 утра, минутная стрелка в четвертый раз поравняется с часовой? Задача 3. Из одной точки круговой трассы, длина которой равна 16 км, в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч и через 40 минут после старта, он опережает второй автомобиль ровно на один круг. Найдите скорость второго автомобиля. Задача 7. С какой частотой вращается тело по окружности, если за любые 2 с тело совершает три полных оборота? В задаче используются величины, связанные со временем; с точки зрения физики – период (частота)
Cлайд 8
Некоторые задачи из курса математики и физики Задача 4. По двум концентрическим окружностям равномерно вращаются две точки. Одна из них совершает полный оборот на 5 с быстрее, чем другая, и поэтому за 1 мин успевает сделать на два оборота больше. Считая, что в начале движения точки находились на одном луче, выходящем из центра окружностей, вычислить величину угла между этими точками через 1 с. Задача 8. Во сколько раз угловая скорость минутной стрелки часов больше угловой скорости часовой стрелки? В задаче используются величины, связанные с углами; с точки зрения физики – угловые величины (угол поворота, угловая скорость)
Cлайд 9
3 типа задач В задаче используются величины, связанные с расстоянием; с точки зрения физики – линейные величины (линейная скорость, длина окружности); В задаче используются величины, связанные со временем; с точки зрения физики – период (частота); В задаче используются величины, связанные с углами; с точки зрения физики – угловые величины (угол поворота, угловая скорость);
Cлайд 10
Рекомендации к решению Условие, применяемое ко всем типам задач: Если в задаче движутся 2 объекта, то следует учитывать скорость сближения или удаления (с точки зрения физики – «относительную скорость»). Величина v t s В одном направлении S В противоположных направлении
Cлайд 11
Рекомендации к решению (I тип) Если в задаче используются величины, связанные с расстоянием; с точки зрения физики – линейные величины (линейная скорость, длина окружности), то задачу можно свести к движению по прямой. Величина v t s Формула
Cлайд 12
Рекомендации к решению (III тип) Если в задаче используются величины, связанные с углами (физически – угловые величины: угол поворота, угловая скорость), то длину окружности можно задать как часть круга: Величина v t s Формула , гдеN– число оборотов
Cлайд 13
Рекомендации к решению (II тип) Если в задаче используются величины, связанные со временем (с точки зрения физики – период или частота), то необходимо учитывать длину окружности. Величина v t s Формула
Cлайд 14
Помогут ли наши рекомендации? Задача 10. Леша, Лена и Юля, стартовав одновременно на 250 – метровой трассе, имеющей форму окружности, бегут в одном направлении. Леша догнал Лену, делая свой третий круг на расстоянии от места старта, а через 20 минут он в третий раз обогнал Юлю. Лена догнала Юлю через полчаса после старта. Найдите скорости школьников. В задаче используются величины, связанные с расстоянием; с точки зрения физики – линейные величины (линейная скорость, длина окружности) – I тип В задаче используются величины, связанные со временем; с точки зрения физики – период (частота) – II тип
Cлайд 15
Решение будем строить на основании рекомендаций по каждому типу Образец Леша - Лена Леша - Юля Лена - Юля
Cлайд 16
Решение будем строить на основании рекомендаций по каждому типу Леша догнал Лену, делая свой третий круг на расстоянии ¼ от места старта через 20 минут Леша в третий раз обогнал Юлю Лена догнала Юлю через полчаса после старта Образец S Для места встречи Леши и Лены Леша Для места встречи Леши и Юли Леша Для места встречи Лены и Юли Лена
Cлайд 17
Величины T1, T2, T3 выражены в таблицах дважды
Cлайд 18
Решение системы: Полученные данные были проверены на практике и получили подтверждение.
Cлайд 19
С помощью составленных таблиц и рекомендация мы быстрее смогли выявить связи между величинами и составить уравнения. Помогли ли наши рекомендации?
Cлайд 20
Заключение Математические и физические методы, используя различную терминологию, при составлении уравнений сводится к одним и тем же смысловым выражениям: линейная скорость, длина окружности, период обращения, частота обращения, угловая скорость и т.д.; При движении нескольких объектов необходимо учитывать скорость сближения или удаления (с точки зрения физики – «относительную скорость»);
Cлайд 21
Заключение: 3 типа задач В задаче используются величины, связанные с расстоянием; с точки зрения физики – линейные величины (линейная скорость, длина окружности); В задаче используются величины, связанные со временем; с точки зрения физики – период (частота); В задаче используются величины, связанные с углами; с точки зрения физики – угловые величины (угол поворота, угловая скорость);
Cлайд 22
Заключение: таблицы связи величин Занесите в таблицу известные величины, а остальные найдите по формулам: Величина v t s В одном направлении s В противоположных направлении s
Cлайд 23
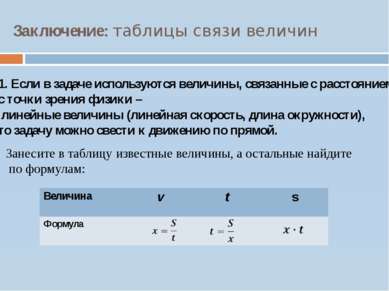Заключение: таблицы связи величин 1. Если в задаче используются величины, связанные с расстоянием; с точки зрения физики – линейные величины (линейная скорость, длина окружности), то задачу можно свести к движению по прямой. Занесите в таблицу известные величины, а остальные найдите по формулам: Величина v t s Формула
Cлайд 24
Рекомендации по решению задач на движение по замкнутой линии 2. Если в задаче используются величины, связанные со временем (с точки зрения физики – период или частота), то необходимо учитывать длину окружности. Формулы для определения величин запишем следующим образом: Величина v t s Формула
Cлайд 25
Рекомендации по решению задач на движение по замкнутой линии 3. Если в задаче используются величины, связанные с углами (физически – угловые величины: угол поворота, угловая скорость), то длину окружности можно задать как часть круга: – пройденное расстояние измеряют в угловых (дуговых) градусах (градусная мера дуги равна градусной мере центрального угла), – а угловую скорость — в градусах за единицу времени (возможно, также — в числе оборотов за единицу времени; один оборот равен 3600). – Формулы для определения величин запишем следующим образом: Величина ω t Формула , гдеN– число оборотов
Cлайд 26
Заключение Практическое применение таблиц для составления уравнений подтверждает целесообразность их применения. Оптимизация процесса решения текстовых задач на движение по замкнутой линии представлена нами в виде рекомендаций к решению задач на движение по замкнутой линии
Cлайд 27
Литература Блинков А. Д., Горская Е. С., Гуровиц В. М. Московские математические регаты. – М. «МЦНМО». 2007 г., - 358 с.; Воронов И.Н., Дорошенко Н.К. Экзаменационные задачи по физике для поступающих в СибГИУ: Учебное пособие. СибГИУ. – Новокузнецк, 2001 г., 200 с.; Кабардин О.Ф., Орлов В.А., Эвенчик Э.Е., Шамаш С.Я., Пинский А.А., Кабардина С.И., Дик Ю.И., Никифоров Г.Г., Шефер Н.И. Физика. 10 класс, М.: «Просвещение», 2007 г.; Открытый банк задач ЕГЭ по математике. Летопись МИФИ [Электронный ресурс] / http://live.mephist.ru/show/mathege2010/view/B12/all/; Цыпкин А.Г., Пинский А.И. Справочное пособие по методам решения задач по математике для средней школы. – М. Наука. Главная редакция физико-математической литературы. 1963 г., - 416 с.;
Cлайд 28
СПАСИБО ЗА ВНИМАНИЕ
