X
Код презентации скопируйте его
Вероятностный подход к определению количества информации
Скачать эту презентацию
Презентация на тему Вероятностный подход к определению количества информации
Скачать эту презентациюCлайд 1
Вероятностный подход к определению количества информации Автор: учитель информатики МБОУ Кулешовской СОШ №17 Азовского района
Cлайд 2
Информация - мера уменьшения неопределённости знаний. Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации. Загадайте целое положительное число до 60. С какой попытки можно точно отгадать ваше число? (Предположим загадали число 3) Это число меньше 30? Это число меньше 15? Это число меньше 8? Это число меньше 4? Это число меньше 2? Это число 2? Вывод: Каждый ответ уменьшал неопределённость в 2 раза. Всего было задано 6 вопросов. Значит, набрано 6 бит информации. Метод половинного деления
Cлайд 3
Задача. Какое минимальное количество бит необходимо для кодирования целых положительных чисел меньших 60 ? Формула вычисления количества информации: N=2I => i=log2N - формула Хартли (1) N - возможное количество равновероятных событий I - количество информации в сообщении о том, что произошло одно из N событий i=log260=5.9 6 бит
Cлайд 4
Какое количество информации будет получено 2-м игроком в игре крестики-нолики на поле 4*4 после 1-го хода первого игрока ? N=2i N=16 => i=4 бит В коробке 16 разноцветных карандашей. Сколько бит информации в сообщении о том, что достали жёлтый карандаш? х
Cлайд 5
"Классическая формула" для вычисления вероятностей. Вероятность события А равна отношению числа благоприятных исходов к числу всех равновероятных исходов: P(A)=m/n, где Р(А) – вероятность события А; n – общее число исходов; m – число исходов, благоприятных событию А. Если все исходы благоприятны для события А, то его вероятность равна 1. Если благоприятных исходов нет, то вероятность события А равна 0. ПРИМЕР 1. Найти вероятность того, что первая же карта, вытащенная из колоды, в которой 36 карт, окажется тузом. РЕШЕНИЕ. Обозначим А событие, состоящее в вытаскивании из колоды туза. Имеем всего 36 равновероятных исходов, т.е. n=36. В каждой из четырёх мастей есть свой туз, таким образом, имеем 4 благоприятных исхода, т.е. m=4. Вероятность вытащить туза P(A)=4/36=1/9. ОТВЕТ. P(A)=1/9.
Cлайд 6
ПРИМЕР 2. В урне находится 2 белых и 3 чёрных шара. Из урны наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет 1)белым; 2)чёрным; 3)зелёным; 4)белым или чёрным? РЕШЕНИЕ. Общее число исходов n=5. 1) Число исходов, благоприятных событию А-"вынут белый шар", m=2. Значит, P(A)=2/5. 2) В-"вынут чёрный шар", m=3, P(B)=3/5. 3) С-"вынут зелёный шар", m=0, P(C)=0. 4) D - "вынут белый или чёрный шар", m=5, P(D)=1. ОТВЕТ. P(A)=2/5, P(B)=3/5, P(C)=0, P(D)=1.
Cлайд 7
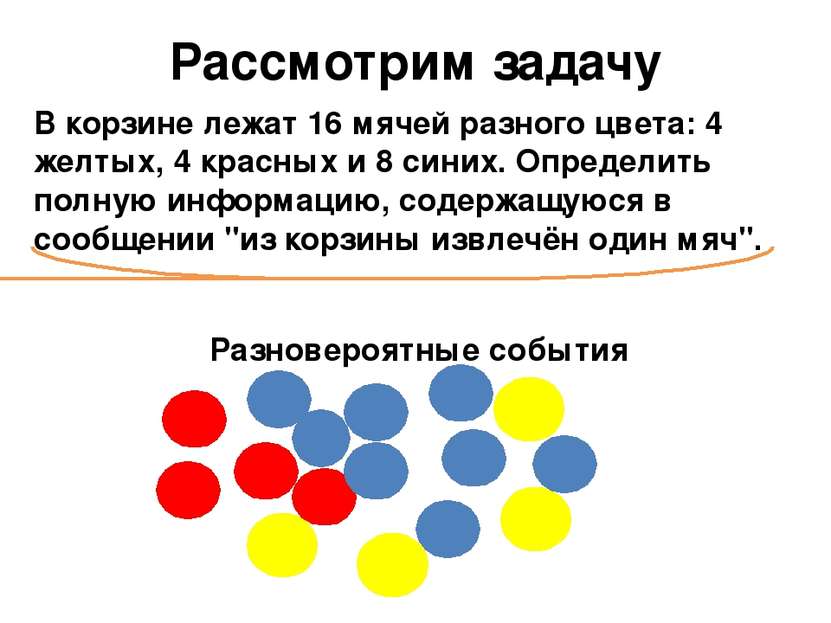
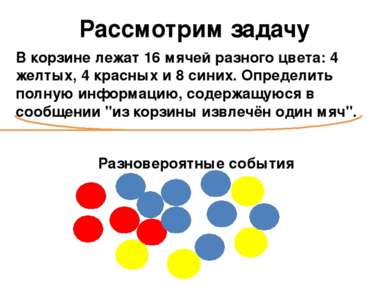Рассмотрим задачу В корзине лежат 16 мячей разного цвета: 4 желтых, 4 красных и 8 синих. Определить полную информацию, содержащуюся в сообщении "из корзины извлечён один мяч". Разновероятные события
Cлайд 8
Формула Шеннона Формулу для вычисления количества информации для событий с различными вероятностями предложил Клод Шеннон в 1948 г. I – количество информации n – количество возможных событий pi – вероятности отдельных событий (2)
Cлайд 9
При этом каждое отдельное слагаемое этой формулы рассматривают как частную информацию, получаемую от отдельного сообщения. (3) Задача. В корзине лежат 16 мячей разного цвета: 4 желтых, 4 красных и 8 синих. Какое количество информации в частных сообщениях о том, что "достали жёлтый мяч", "достали красный мяч", "достали синий мяч". Решение. Система, состояние которой выясняется, имеет три возможных состояния: х1-достали жёлтый мяч, х2- достали красный мяч, х3- достали синий мяч. Вероятности этих состояний: p1=4/16=1/4, p2=4/16=1/4, p3=8/16=1/2. В задаче требуется найти частную информацию от сообщений, поэтому применим формулу (3). Iх1=-log2(1/4)=2(бита), Iх2=-log2(1/4)=2(бита), Iх3=-log2(1/2)=1(бит) Ответ. I1=2 бита, I2=2 бита, I3=1 бит.
Cлайд 10
Задача. В корзине лежат 16 мячей разного цвета: 4 желтых, 4 красных и 8 синих. Определить полную информацию, содержащуюся в сообщении «из корзины извлечён один мяч». Решение. Система, состояние которой выясняется, имеет три возможных состояния: х1-достали жёлтый мяч, х2- достали красный мяч, х3- достали синий мяч. Вероятности этих состояний: p1=4/16=1/4, p2=4/16=1/4, p3=8/16=1/2. В задаче требуется найти полную информацию от сообщений, поэтому применим формулу (2). Ix=-(1/4*log2(1/4)+1/4*log2(1/4)+1/2*log2(1/2))=1,5(бита) Ответ. Ix=1,5 бита.
Cлайд 11
Решите задачи Задача 1. В корзине лежат 20 яблок, 10 груш и 10 слив. Сколько бит информации несёт частное сообщение о том, что выбранный из корзины фрукт - яблоко? Задача 2. В корзине лежат 20 яблок, 10 груш и 10 слив. Сколько бит информации несёт полное сообщение о том, что из корзины извлечён один фрукт?
