X
Код презентации скопируйте его
Симметрия
Скачать эту презентацию
Презентация на тему Симметрия
Скачать эту презентациюCлайд 1
Симметрия Выполнили: Леонтьева Диана, Грязина Эльвира МБОУ СОШ №92 2014 г.
Cлайд 2
«Симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Математически строгое представление о симметрии сформировалось сравнительно недавно - в 19 веке. В наиболее простой трактовке современное определение симметрии выглядит примерно так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали (Г.Вейлю). Виды симметрии: центральная симметрия (или симметрия относительно точки) осевая симметрия (или симметрия относительно прямой) зеркальная симметрия скользящая симметрия винтовая симметрия
Cлайд 3
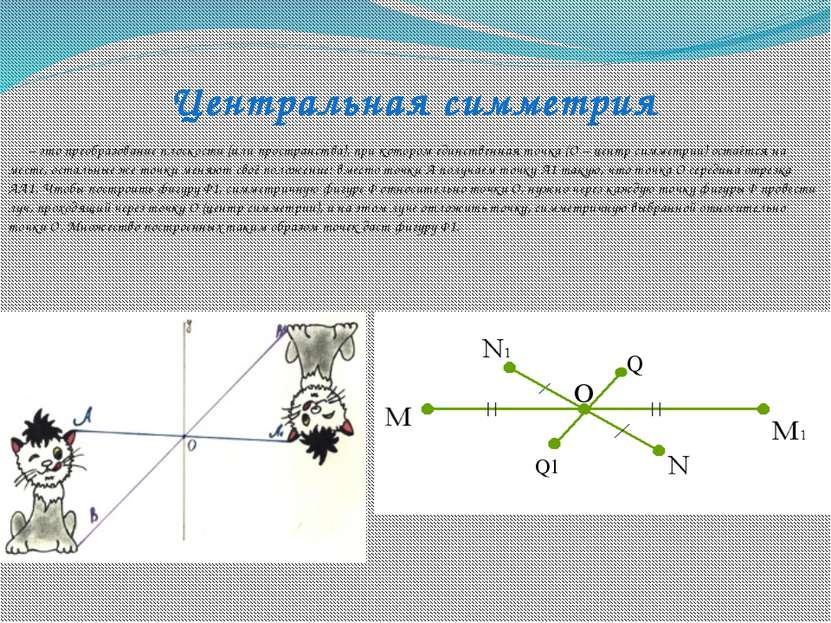
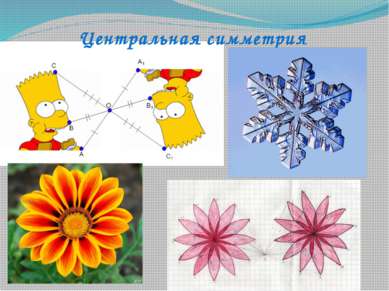
– это преобразование плоскости (или пространства), при котором единственная точка (О – центр симметрии) остаётся на месте, остальные же точки меняют своё положение: вместо точки А получаем точку А1 такую, что точка О середина отрезка АА1. Чтобы построить фигуру Ф1, симметричную фигуре Ф относительно точки О, нужно через каждую точку фигуры Ф провести луч, проходящий через точку О (центр симметрии), и на этом луче отложить точку, симметричную выбранной относительно точки О. Множество построенных таким образом точек даст фигуру Ф1. Центральная симметрия O Q Q1
Cлайд 4
Центральная симметрия
Cлайд 5
– это преобразование плоскости (или пространства), при котором только точки прямой р остаются на месте (эта прямая является осью симметрии), остальные же точки меняют своё положение: вместо точки В получаем такую точку В1, что прямая р является серединным перпендикуляром к отрезку ВВ1. Чтобы построить фигуру Ф1, симметричную фигуре Ф, относительно прямой р, нужно для каждой точки фигуры Ф построить точку, симметричную ей относительно прямой р. Множество всех этих построенных точек и дают искомую фигуру Ф1. Осевая симметрия
Cлайд 6
Осевая симметрия
Cлайд 7
– это преобразование пространства, при котором только точки одной плоскости сохраняют своё местоположение (α-плоскость симметрии), остальные точки пространства меняют своё положение: вместо точки С получается такая точка С1, что плоскость α проходит через середину отрезка СС1, перпендикулярно к нему. Чтобы построить фигуру Ф1,симметричную фигуре Ф относительно плоскости α, нужно для каждой точки фигуры Ф выстроить симметричные относительно α точки, они в своём множестве и образуют фигуру Ф1. Зеркальная симметрия
Cлайд 8
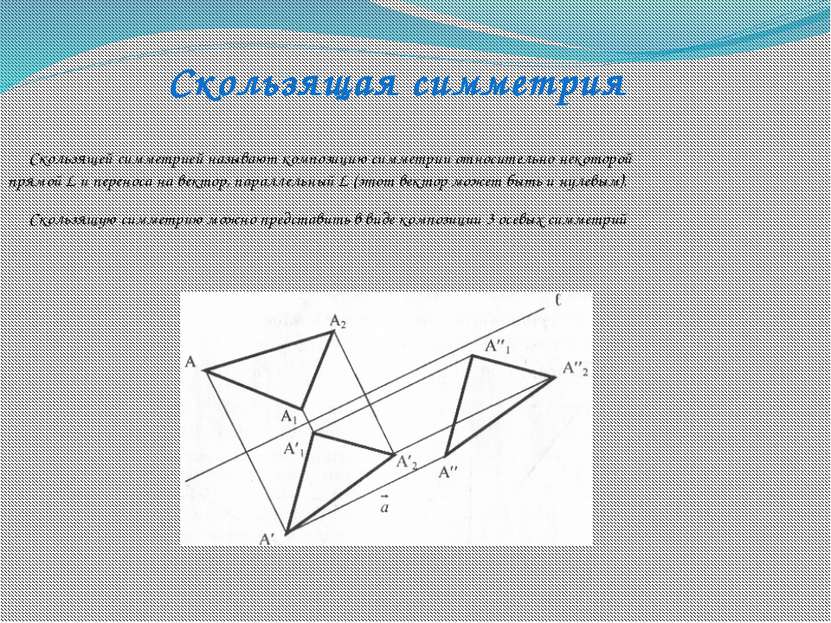
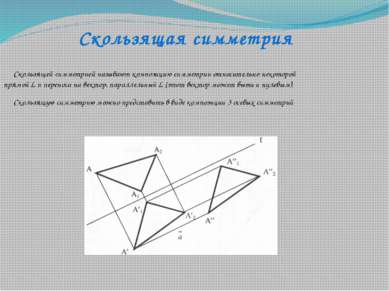Скользящей симметрией называют композицию симметрии относительно некоторой прямой L и переноса на вектор, параллельный L (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий Скользящая симметрия
Cлайд 9
— это симметрия объекта относительно группы преобразований, являющихся композицией преобразования поворота объекта вокруг оси и переноса его вдоль этой оси. Винтовая симметрия
Cлайд 10
А Д Л М П Т Ф Ш – вертикальная ось В Е З К С Э Ю - горизонтальная ось Палиндромы: Доход, казак, мадам, комок, радар, шалаш, потоп и др. А роза упала на лапу Азора. Хил, худ, а дух лих. Леша на полке клопа нашел. Нажал кабан на баклажан. У дуба буду. Он в аду давно. Симметрия в русском языке и литературе
Cлайд 11
Симметрия в физике и химии Молекула воды симметрия электрического и магнитного полей
Cлайд 12
Симметрия в искусстве
Cлайд 13
Симметрия в архитектуре
Cлайд 14
Cлайд 15
Симметрия в природе
Cлайд 16
