X
Код презентации скопируйте его
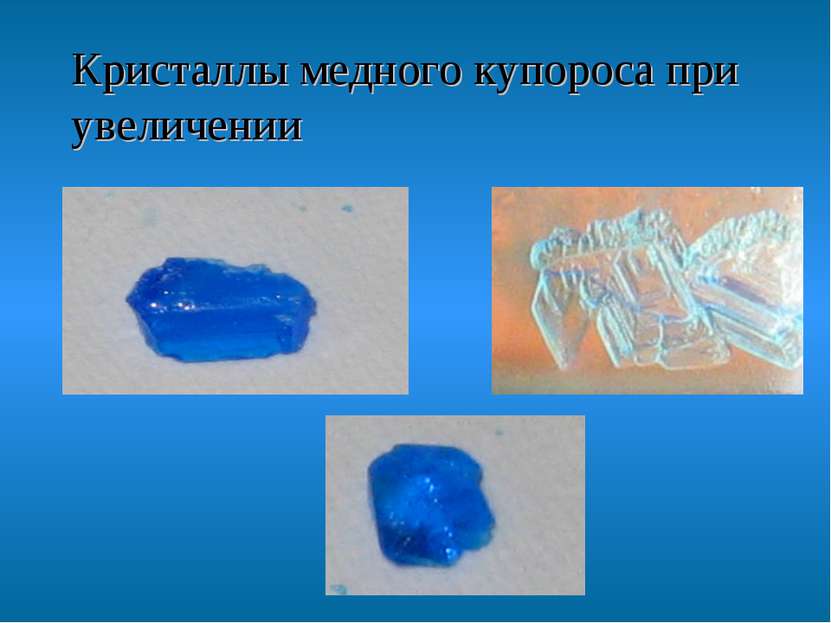
Симметрия в мире химии: кристаллы
Скачать эту презентацию
Презентация на тему Симметрия в мире химии: кристаллы
Скачать эту презентациюCлайд 1
Гимназия № 399 Исследовательская работа на тему: «Симметрия в мире химии : кристаллы» Выполнена учащейся 9 «А» класса гимназии № 399 Демчук Анастасией Научные руководители: Морозова Наталья Михайловна, учитель математики Анацко Ольга Эдуардовна, учитель химии Санкт-Петербург 2005/2006 учебный год
Cлайд 2
Задачи исследования: Дать определение симметрии Определить виды симметрии Рассмотреть химические объекты - кристаллы Выяснить, как проявляются различные виды симметрии на примере кристаллов Провести синтез кристаллов ряда веществ Цель исследования: Выявить, как проявляются различенные виды симметрии при рассмотрении различных кристаллов.
Cлайд 3
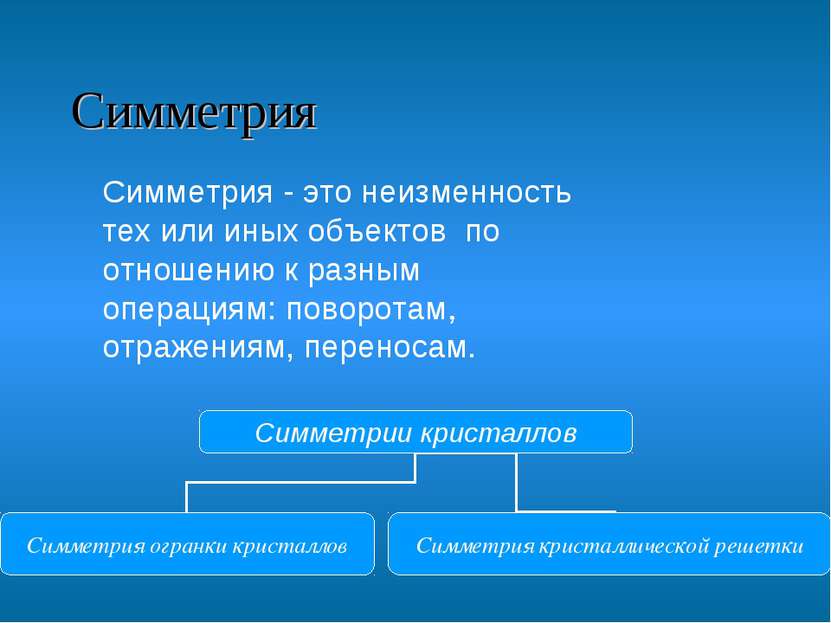
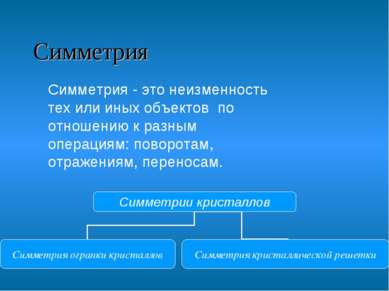Симметрия Симметрия - это неизменность тех или иных объектов по отношению к разным операциям: поворотам, отражениям, переносам. Симметрия - это неизменность тех или иных объектов по отношению к разным операциям: поворотам, отражениям, переносам. .
Cлайд 4
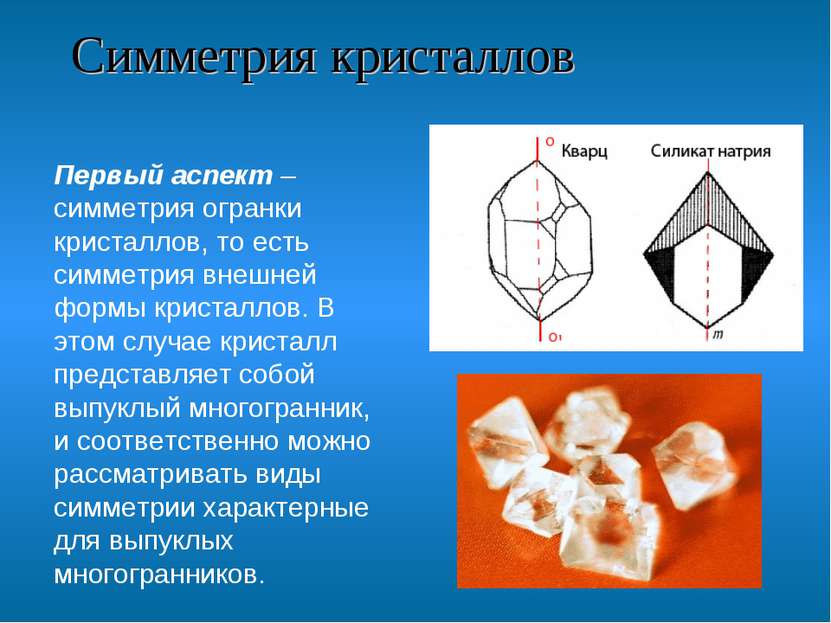
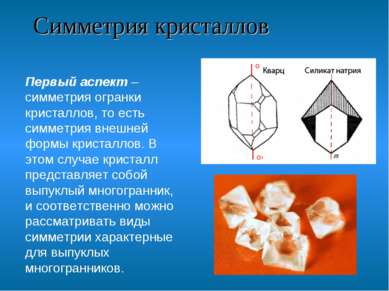Симметрия кристаллов Первый аспект – симметрия огранки кристаллов, то есть симметрия внешней формы кристаллов. В этом случае кристалл представляет собой выпуклый многогранник, и соответственно можно рассматривать виды симметрии характерные для выпуклых многогранников.
Cлайд 5
Симметрия кристаллов – снежные кристаллы
Cлайд 6
Симметрия кристаллов Второй аспект - симметрия кристаллической решетки, которая определяет внешнюю форму кристалла.
Cлайд 7
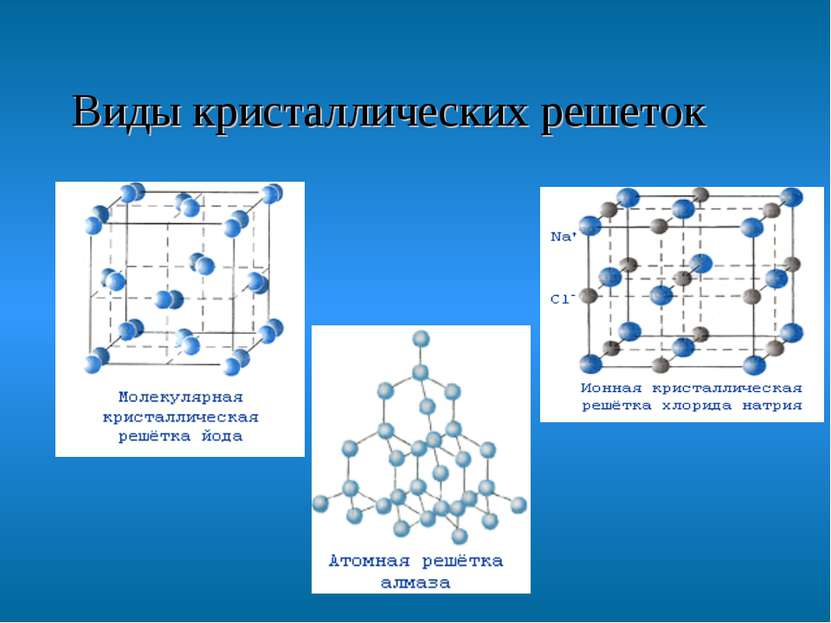
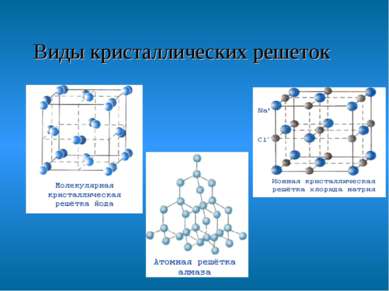
Симметрия кристаллов Кристаллическая решётка - периодически повторяющаяся в пространстве структура из атомов, молекул или ионов.
Cлайд 8
Виды кристаллических решеток
Cлайд 9
Виды кристаллических решеток
Cлайд 10
В кристаллических решетках проявляются следующие виды симметрии: Трансляционная симметрия Различные виды осевой симметрии Симметрия относительно плоскости Винтовая симметрия Центральная симметрия.
Cлайд 11
Трансляционная симметрия Трансляционная симметрия – симметричность относительно сдвигов в пространстве в каком-либо направлении на некоторое расстояние. Симметрия относительно прямой Каждая точка М переходит в точку М' такую, что отрезок ММ' перпендикулярен прямой а и делится ею пополам.
Cлайд 12
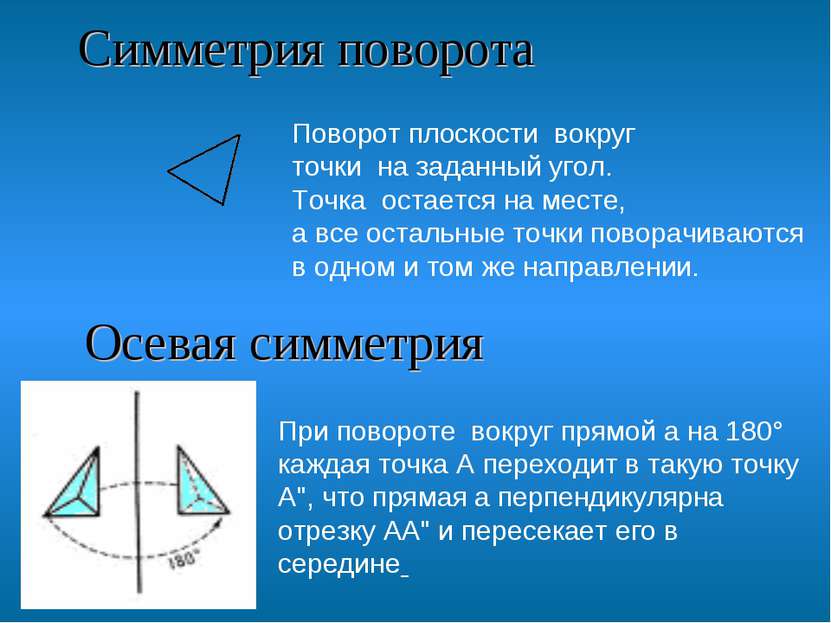
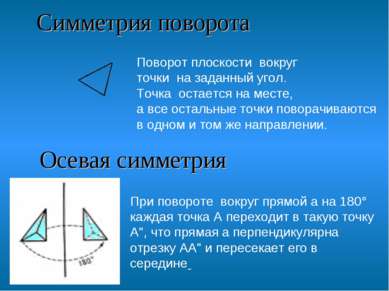Симметрия поворота Поворот плоскости вокруг точки на заданный угол. Точка остается на месте, а все остальные точки поворачиваются в одном и том же направлении. Осевая симметрия При повороте вокруг прямой a на 180° каждая точка A переходит в такую точку A", что прямая a перпендикулярна отрезку AA" и пересекает его в середине
Cлайд 13
Центральная симметрия Центральная симметрия - симметрия относительно точки О — преобразование плоскости, при котором каждая точка М переходит в точку М‘ такую, что отрезок ММ' проходит через точку О и делится ею пополам.
Cлайд 14
Зеркальная симметрия Плоская фигура, преобразующаяся в себя при зеркальном отражении, симметрична относительно прямой — оси симметрии.
Cлайд 15
Винтовая симметрия Винтовой симметрией называется композиция поворота и переноса на вектор параллельно оси поворота.
Cлайд 16
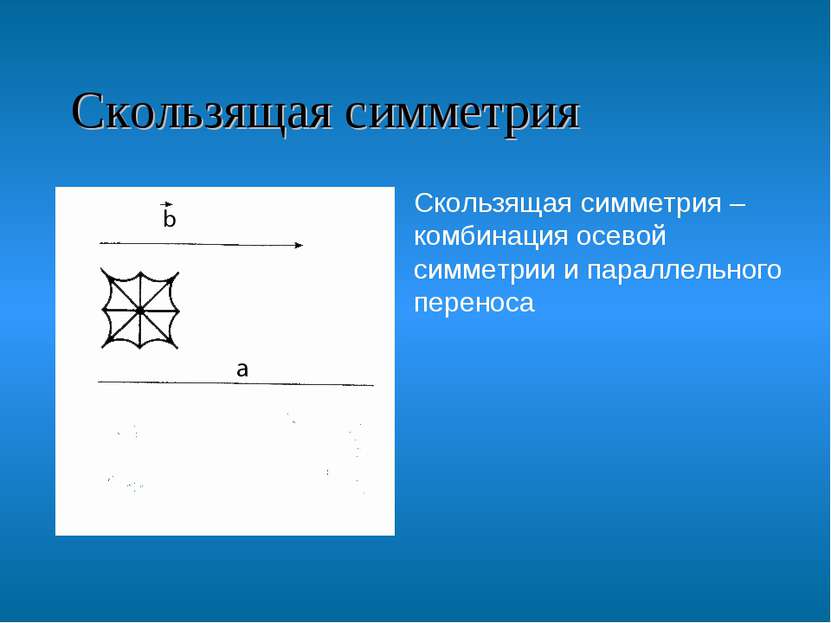
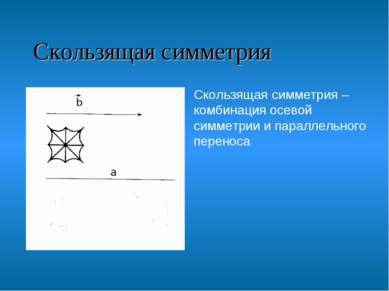Скользящая симметрия Скользящая симметрия – комбинация осевой симметрии и параллельного переноса
Cлайд 17
Симметрия параллельного переноса Симметрией переноса называется симметрия, при которой фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса).
Cлайд 18
Правильные многогранники Правильными называют такие многогранники, у которых все грани - правильные равные многоугольники и в каждой вершине сходится одно и тоже число ребер.
Cлайд 19
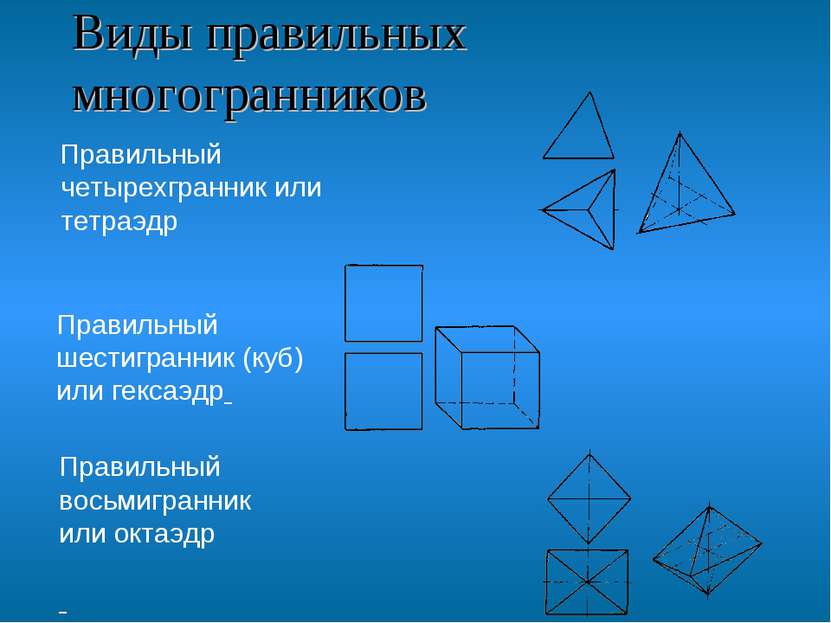
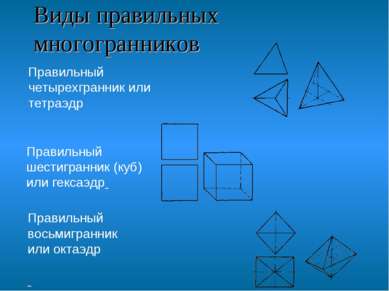Виды правильных многогранников Правильный четырехгранник или тетраэдр Правильный шестигранник (куб) или гексаэдр Правильный восьмигранник или октаэдр
Cлайд 20
Виды правильных многогранников Правильный двенадцатигранник или додекаэдр Правильный двадцатигранник или икосаэдр
Cлайд 21
Экспериментальная часть Мы проводили синтез кристаллов хлорида натрия и медного купороса в домашних условиях.
Cлайд 22
Кристаллы медного купороса при увеличении
Cлайд 23
Выводы В мире кристаллов - проявляются все основные виды симметрии 2. На примерах кристаллов различных веществ можно проследить все свойства абстрактных фигур – многогранников.
