X
Код презентации скопируйте его
Симметрия вооруженным глазом
Скачать эту презентацию
Презентация на тему Симметрия вооруженным глазом
Скачать эту презентациюCлайд 1
МОУ Сосновская сош № 2 МОЗГОВА ЕКАТЕРИНА
Cлайд 2
Cлайд 3
Мир, в котором мы живем, наполнен геометрией домов и улиц,
Cлайд 4
«Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство» Герман Вейль ЦЕЛЬ работы : Рассмотреть здания на улицах поселка. Найти закономерность построек симметричных и асимметричных домов с учетом времени их строительства. Изучить, как в архитектурных строениях сочетается симметрия, красота и удобство.
Cлайд 5
В древности слово «симметрия» употреблялось как «гармония», «красота». Симметрия – греческое слово, обозначающее соразмерность, пропорциональность, одинаковость в расположении частей предмета по противоположным сторонам от точки , прямой или плоскости. Предметы, обладающие такими свойствами, называются симметричными.
Cлайд 6
Что такое симметрия? Симметрией называется закономерная повторяемость в расположении предметов или их частей на плоскости или в пространстве Симметрия в широком смысле – инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований. Лежит в основе законов сохранения Асимметрия – это свойство геометрических фигур не способных к отображению. Нарушенную, частично расстроенную симметрию называют диссимметрией.
Cлайд 7
Разновидности симметрии Различают три вида симметрии : симметрия относительно прямой симметрия относительно точки симметрия относительно плоскости
Cлайд 8
Осевая, центральная и отображающая пространство на себя симметрия Симметрия относительно прямой называется осевой симметрией Симметрия относительно точки называется центральной симметрией Симметрия относительно плоскости называется отображение пространства на себя
Cлайд 9
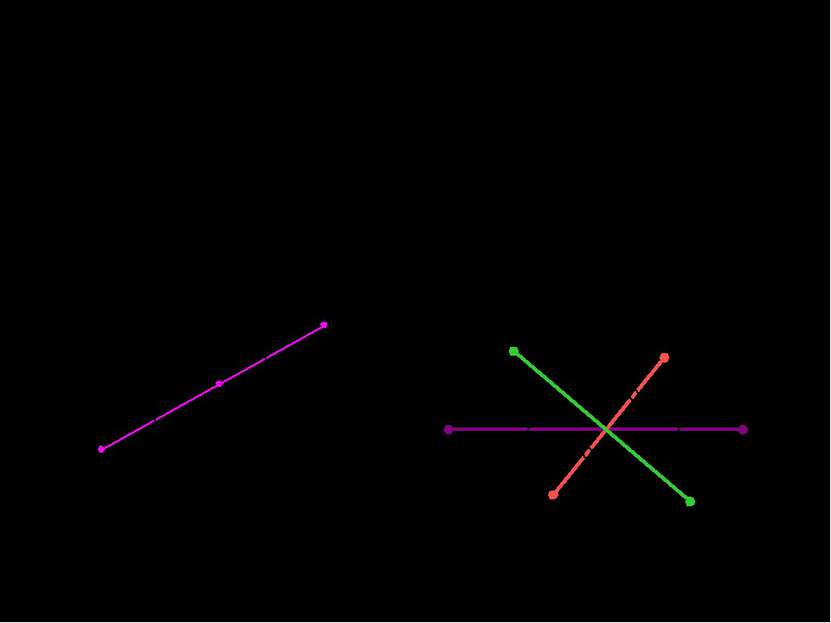
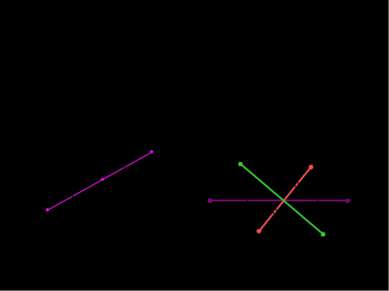Центральная симметрия Точки А1 и А2 называются симметричными относительно точки О, если О – середина отрезка А1А2 А1 А2 О О Р Q M M1 N N1 А1О = ОА2 Точка О – центр симметрии
Cлайд 10
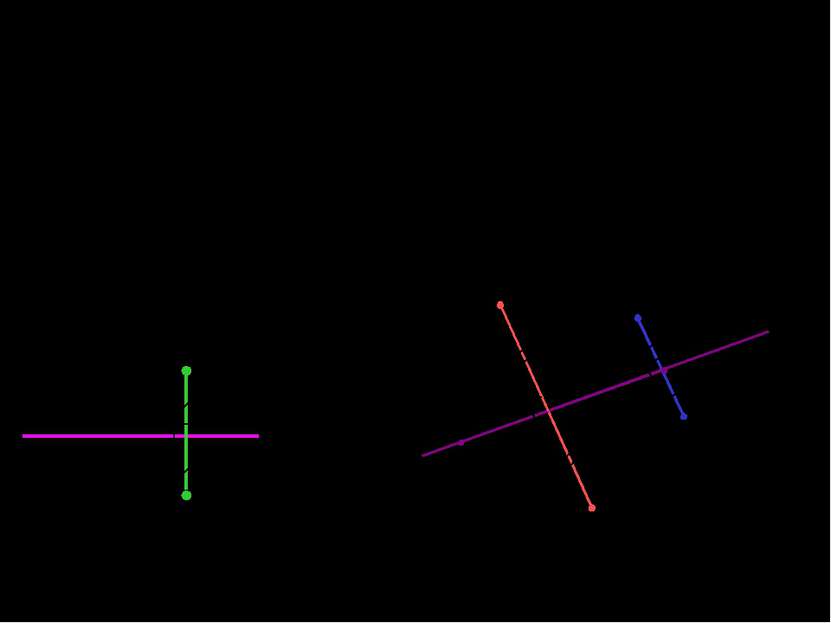
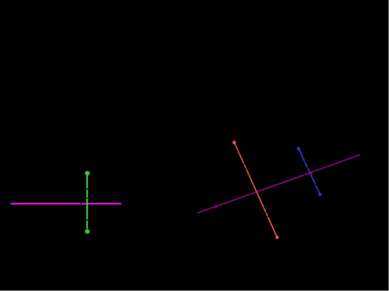Осевая симметрия Точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. а А А1 а – ось симметрии А1 = Sа(А) Р М М1 b N N1 Точка Р симметрична самой себе относительно прямой b
Cлайд 11
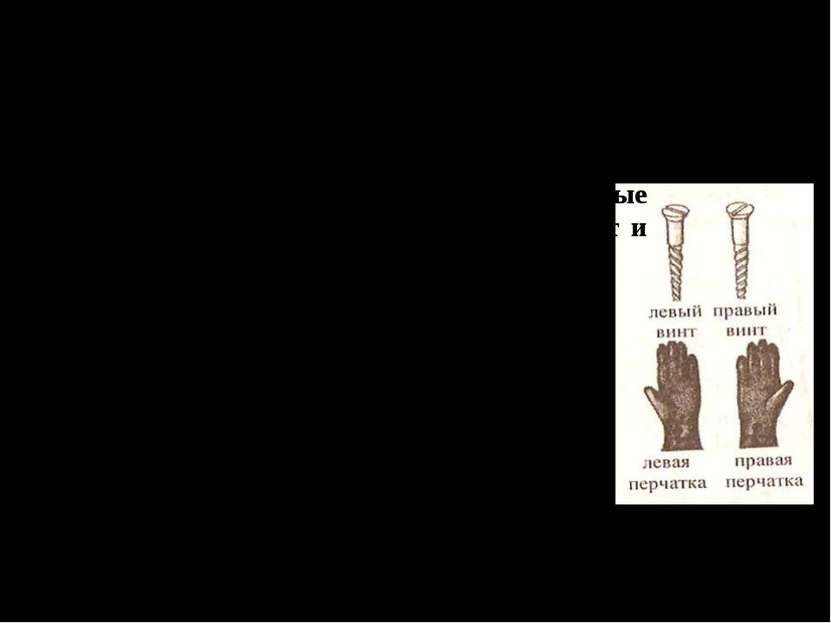
Зеркальная симметрия «Что может быть больше похоже на мою руку или мое ухо, чем их собственное отражение в зеркале? И все же руку, которую я вижу в зеркале «нельзя поставить на место настоящей руки…» Иммануил Кант Плоскостью симметрии P называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение.
Cлайд 12
«Есть в математике нечто вызывающее восторг» Хаусдорф Ф. Есть предположение, что Пифагор понятие золотого сечения позаимствовал у египтян и вавилонян. И, действительно пропорции пирамиды Хеопса, барельефы предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношением золотого сечения при их создании. Пирамида Хеопса
Cлайд 13
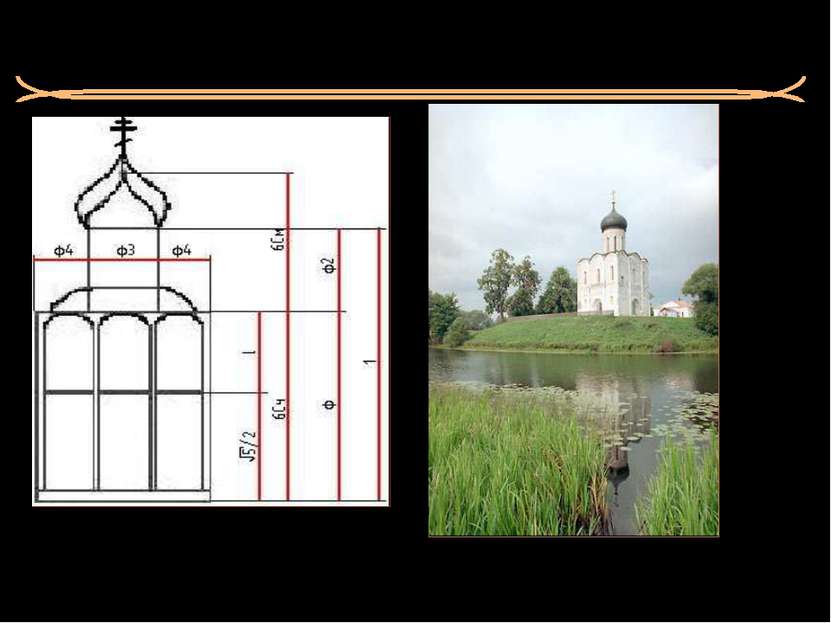
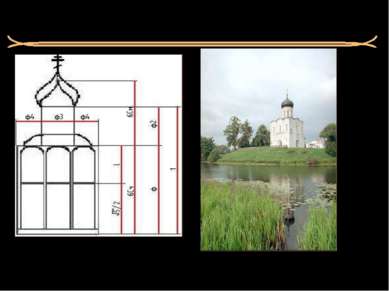«Гёте удачно назвал благородный собор «окаменелой музыкой», …» Юнг Д. Церковь Покрова Богородицы на Нерли 1165 год «Простая» красота пропорций золотого сечения.
Cлайд 14
«…, но, быть может, ещё лучше было бы назвать такой собор «окаменелой математикой» Юнг Д. Пропорции Покровского Собора на Красной площади в Москве определяются восемью членами ряда золотого сечения: Многие члены ряда золотого сечения повторяются в затейливых элементах храма многократно:
Cлайд 15
Симметрия в архитектуре Архитектура – это искусство проектировать и строить здания и другие сооружения (также их комплексы), создающие организованную среду, необходимую людям для их жизни и деятельности В архитектуре очень важна симметрия. Например, если при постройке здания не будет соблюдаться симметрия, то здание либо разрушится, либо будет некрасивым Симметрия также используется в архитектурных композициях, ансамблях, которые имеют декоративное значение (фонтаны, лестницы, ограды)
Cлайд 16
Виды симметрии в архитектурной композиции: центрально-осевая зеркальная; симметрия относительно диагонали; винтовая симметрия.
Cлайд 17
Симметрией в архитектуре мы называем одинаковое расоложение равных частей по отношению к плоскости или линии. Она относится к числу наиболее сильных средств организации формы. Симметричность строения является одной из причин ее активного воздействия на восприятие.
Cлайд 18
В основе композиций большинства произведений зодчества лежат симметрия и асимметрия. Нарушенную, частично расстроенную симметрию мы называем диссимметрией. Асимметрия — отсутствие симметрии. Асимметричная композиция может складываться из симметричных частей, связи между которыми не подчиняются закономерностям симметрии.
Cлайд 19
АСИММЕТРИЯ СЛУЖИТ ИСХОДНЫМ ПУНКТОМ И В АРХИТЕКТУРЕ, НА КАЖДОМ ИЗ ЭТАПОВ ЕЁ РАЗВИТИЯ; ИМЕННО С НЕЙ СВЯЗАН ПРОЦЕСС ПОИСКА КРАСОТЫ, КОМФОРТА И ИСТИНЫ. Единство симметрии и асимметрии заключается и в том, что они предшествуют одна другой. Поиск новых форм симметрии интуитивно связан со стремлением к порядку, гармонии.
Cлайд 20
Использование симметрии и асимметрии в строительстве на основе некоторых улиц пос. Сосновское. Улица, год постройки Симметрия в архитектуре (количество домов) Асимметрия в архитектуре (количество домов) Ул. Луговая 1960 год 20 (4 реконструкция 2005-2010года) 19 (6 реконструкция 2005-2010года) Ул. Зеленая 1980 год 18 9 (5 реконструкция 2005-2010года) Ул. Есенина, Сосновая 1990-2000 год 15 12
Cлайд 21
Симметрия встречается не только в математике, но и в архитектуре и природе, применение категорий симметрии и асимметрии, очевидно, приведет к возникновению новых стилей и видов архитектурных строений. Все архитектурные строения имеют симметричный и асимметричный вид ( примерно по 50%). Симметричные строения делают не только отдельные предметы красивыми, но придает красоту окружающей нас природе и способствует наилучшему зрительному восприятию
Cлайд 22
Дома, выполненные в комбинации нескольких форм красивы и удобны. Простая симметричная архитектура по сей день остается одной из предпочитаемых. Большой и симметричный наклон крыши не позволяет осадкам накапливаться. Симметричность и диссиметричность играют важную роль в устойчивости, освещенности, комфорте и вентиляции жилого дома. Выводы:
Cлайд 23
«Да, путь познания не гладок, Но знаем мы со школьных лет: Загадок больше, чем разгадок И поискам предела нет!» Татьяничева Л.
