X
Код презентации скопируйте его
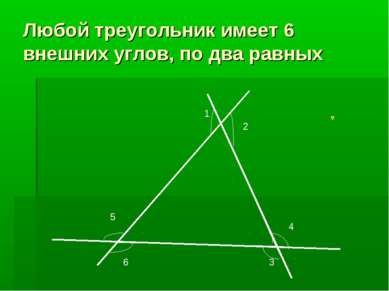
Теорема о сумме углов треугольника
Скачать эту презентацию
Презентация на тему Теорема о сумме углов треугольника
Скачать эту презентациюCлайд 1
МБОУ «Большеигнатовская средняя общеобразовательная школа» Тема урока «Теорема о сумме углов треугольника» Пьянзина В.И. – учитель математики
Cлайд 2
Цели урока: Доказательство теоремы о сумме углов треугольника и следствия из нее; Введение понятий остроугольного, тупоугольного и прямоугольного треугольников; Применение полученных знаний при решении задач; Развитие элементов геометрического мышления.
Cлайд 3
Ход урока. I. Устная работа А) Ответить на вопросы : 1) Какие прямые называются параллельными? Какие отрезки называются параллельными? 2) Сформулировать признаки параллельности прямых. 3) Сформулировать свойства параллельных прямых. 4) Сформулировать определение треугольника и назвать его элементы.
Cлайд 4
Б. Виды треугольников:
Cлайд 5
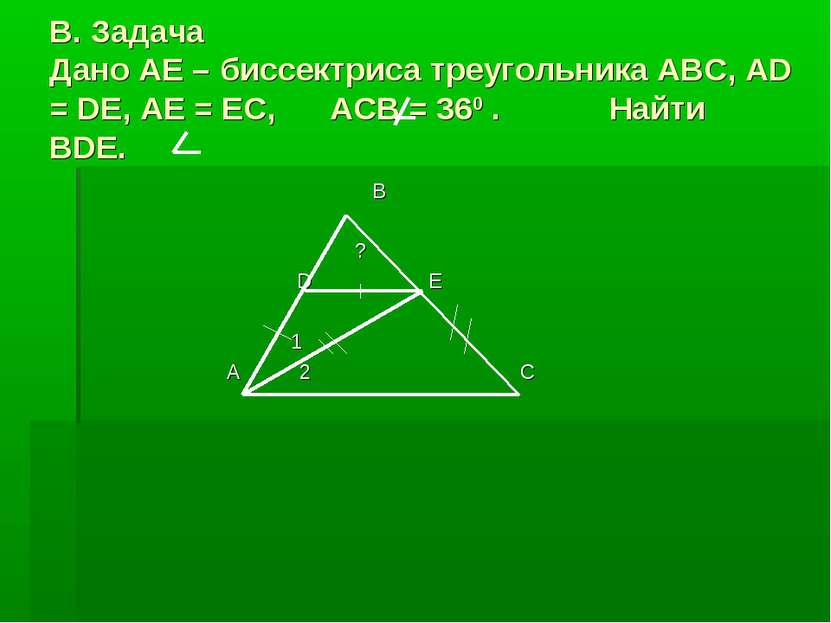
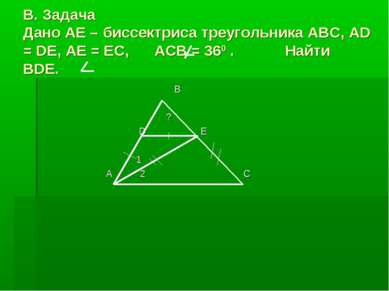В. Задача Дано AE – биссектриса треугольника ABC, AD = DE, AE = EC, ACB = 360 . Найти BDE. B ? D E 1 А 2 C
Cлайд 6
II. Изучение нового материала. Практическая работа: Начертить треугольник и найти сумму углов треугольника (с помощью транспортира); первый ряд – остроугольный, второй ряд – тупоугольный, третий ряд – прямоугольный.
Cлайд 7
2.Какие результаты получили, измеряя транспортиром углы треугольника? Вывод: сумма углов треугольников близка к 1800 .
Cлайд 8
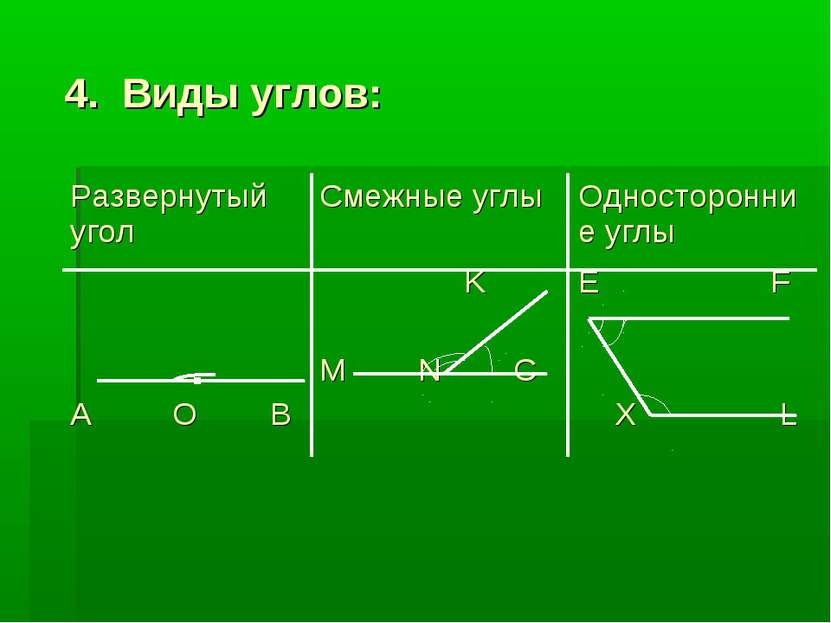
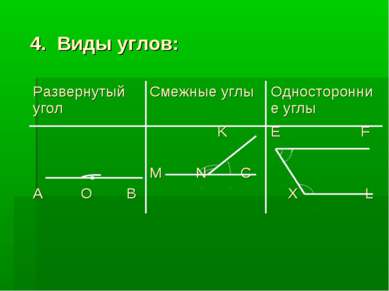
3.Где встречали это число? 1. Величина развернутого угла 1800 2. Сумма смежных углов равна 1800 3.Сумма односторонних углов равна 1800
Cлайд 9
4. Виды углов:
Cлайд 10
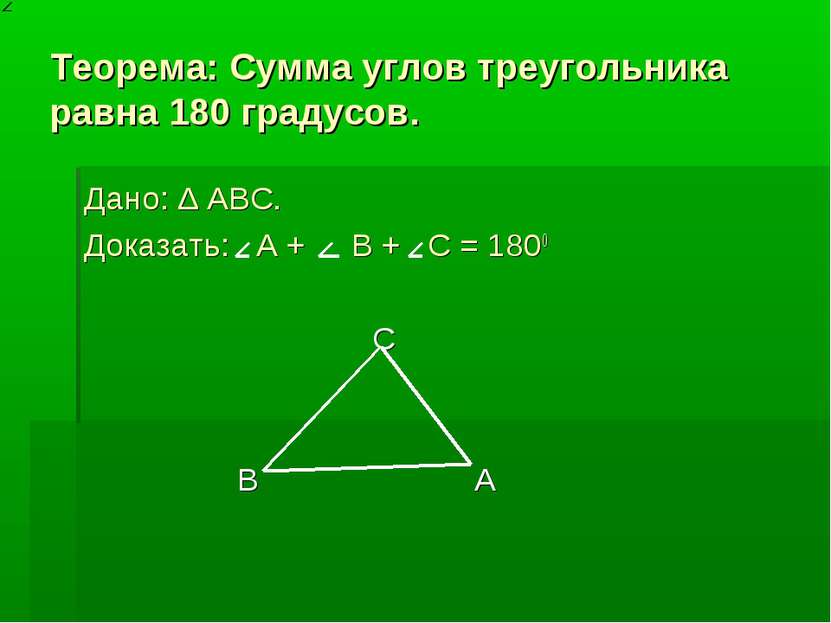
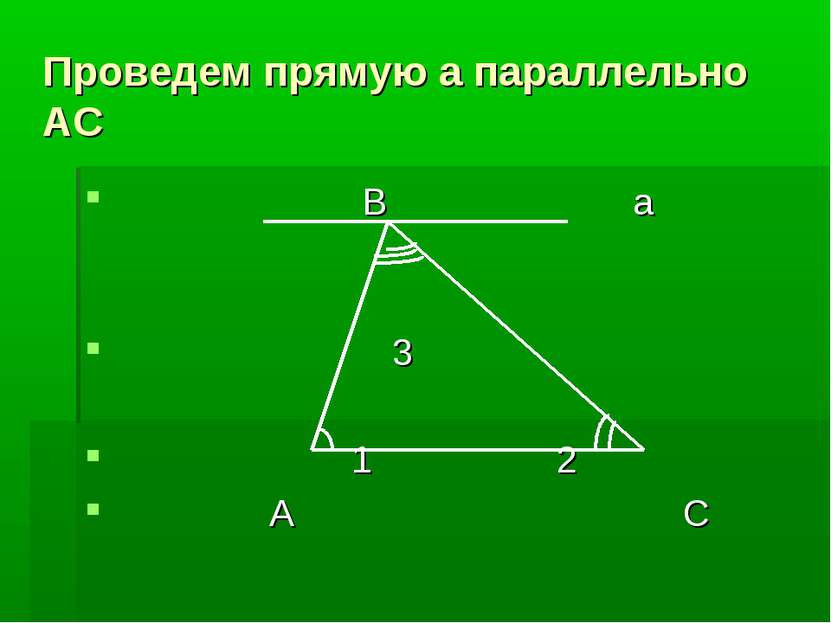
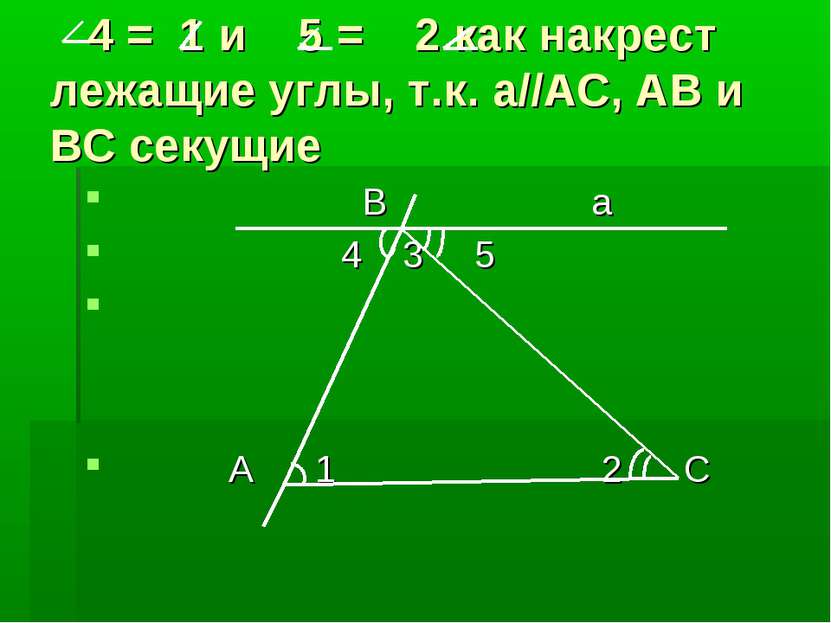
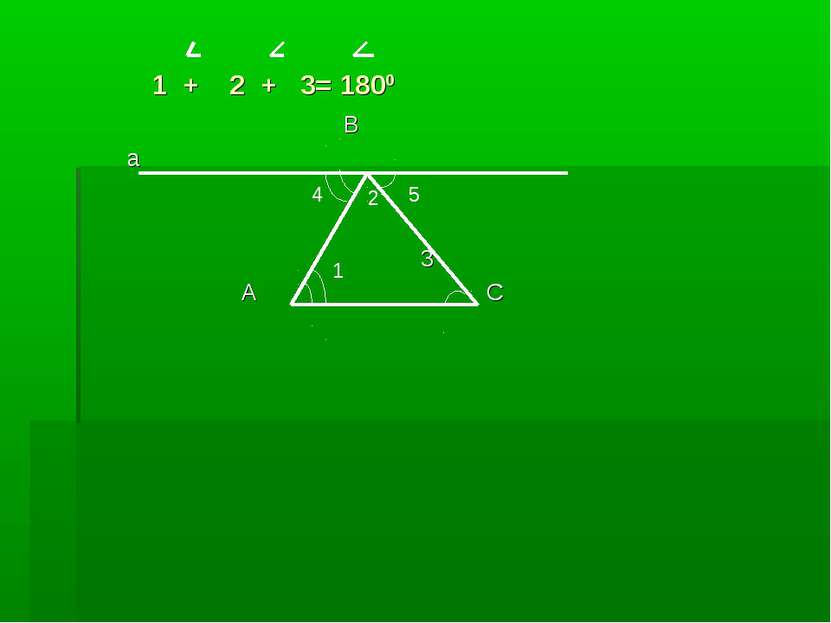
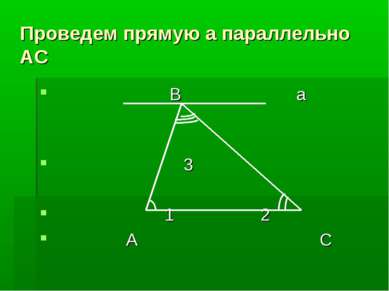
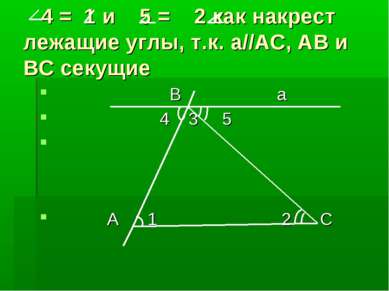
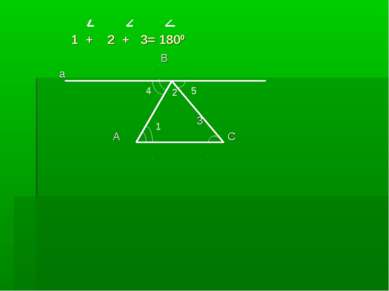
Теорема: Сумма углов треугольника равна 180 градусов. Дано: ∆ ABC. Доказать: А + B + C = 1800 C B A
Cлайд 11
Проведем прямую а параллельно АС В а 3 1 2 А С
Cлайд 12
4 = 1 и 5 = 2 как накрест лежащие углы, т.к. а//АС, АВ и ВС секущие В а 4 3 5 А 1 2 С
Cлайд 13
1 + 2 + 3= 1800 В а 3 А С 1 2 5 4
Cлайд 14
Угол, смежный с каким-нибудь углом треугольника называется внешним углом А В С Д 4 3
Cлайд 15
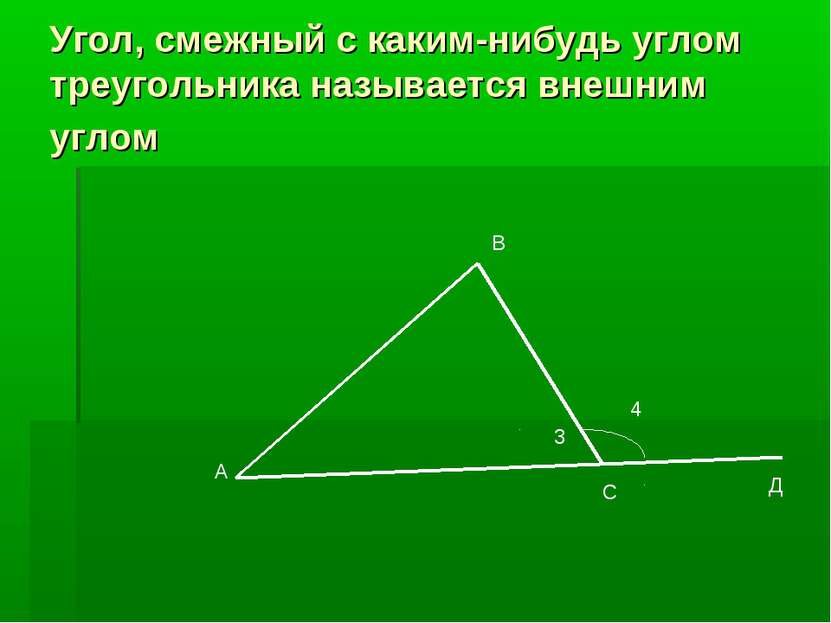
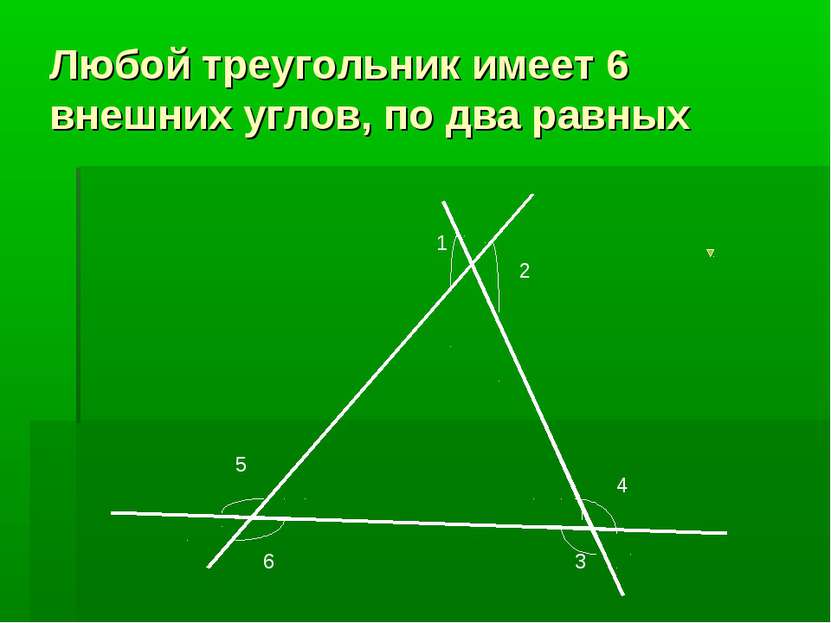
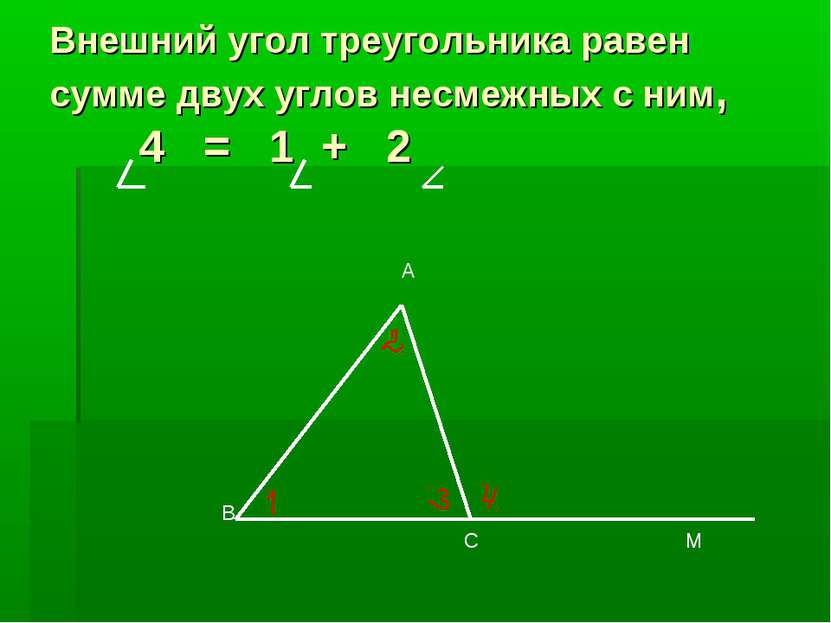
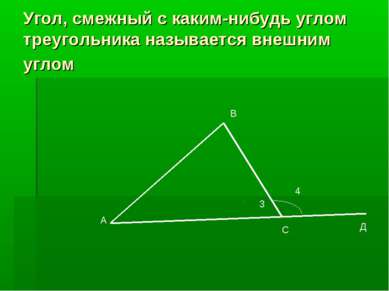
Практическая работа 1. Начертить треугольник и построить все внешние углы. 2. Сколько внешних углов можно построить у одного треугольника? 3. Какого вида могут быть внешние углы? 4. Всегда ли внешний угол тупой? 5.Могут ли все внешние углы быть тупыми? Острыми? 6 .Могут ли все внешние углы быть равными?
Cлайд 16
Любой треугольник имеет 6 внешних углов, по два равных 1 2 4 3 5 6
Cлайд 17
Внешний угол треугольника равен сумме двух углов несмежных с ним, 4 = 1 + 2 А В С М
Cлайд 18
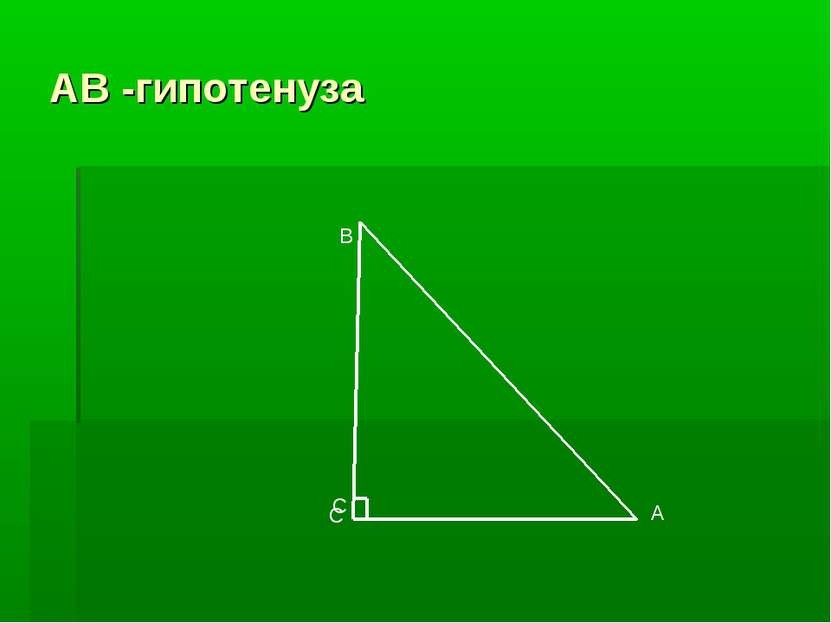
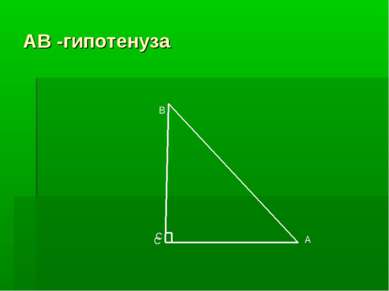
Остроугольные, тупоугольные, прямоугольные треугольники. 1. Остроугольный треугольник – имеет три острых угла. 2. Тупоугольный – один тупой угол. 3. Прямоугольный – один прямой угол. В прямоугольном треугольнике – два катета и гипотенуза, гипотенуза лежит против прямого угла.
Cлайд 19
АВ -гипотенуза С А С В
Cлайд 20
Физкультминутка Если устают глаза, снижается ваше внимание и активность, то давайте дадим отдых глазам и себе. 1.Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза. 2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3-4 раза. 3.Медленно наклоняйте голову: вперед – влево – вправо - назад. Повторите 3-4 раза. 4.Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.
Cлайд 21
Ответить на вопросы: 1. Если один из углов треугольника прямой, то какими будут два других угла? 2. Если треугольник прямоугольный, то чему равна сумма острых углов треугольника? 3. Если один из углов треугольника тупой, то чему равна сумма двух других углов? 4.Могут ли все три угла треугольника быть равными? 5. Чему равна градусная мера каждого из них? 6. Могут ли все углы треугольника быть острыми?
Cлайд 22
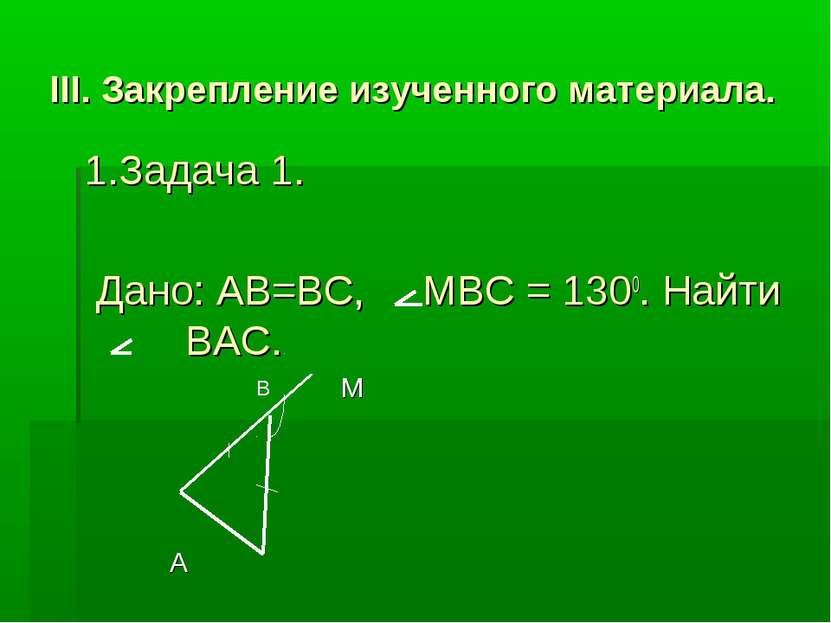
III. Закрепление изученного материала. 1.Задача 1. Дано: AB=BC, MBC = 1300. Найти BAC. M A C В
Cлайд 23
Решение задачи 1. Так как АВ=ВС, то АВС – равнобедренный, значит, А = С. МВС внешний угол АВС, МВС = А + С = 130 º. А + С= 130 º. А = С =130 º : 2 = 65 º ВАС = 65 º .
Cлайд 24
2. Задача №2 Найти углы треугольника АВС, если углы треугольника относятся как 3:5:10.
Cлайд 25
Решение задачи №2 1). 3+5+10=18 2).180º :18=10º 3).10º *3=30º 4).10º *5=50º 5).10º *10=100º
Cлайд 26
3. № 225 Доказать, что каждый угол равностороннего треугольника равен 60 º
Cлайд 27
4. Самостоятельная работа Найти углы треугольника, если углы относятся, как: Вариант 1 - 5:6:7; Вариант 2 – 3:4:2 Вариант 3 - 5:2:2 ;
Cлайд 28
Проверка самостоятельной работы: Вариант 1 50º ; 60º ; 70º : Вариант 2 60º ; 80º ; 40º ; Вариант 3 100º ; 40º ; 40º ;
Cлайд 29
IV. Итог урока. Задание на дом: П. 30, № 223 (в,г), 235, 234
