X
Код презентации скопируйте его
Плоскость
Скачать эту презентацию
Презентация на тему Плоскость
Скачать эту презентациюCлайд 1
Проекции плоскости Лекция 3
Cлайд 2
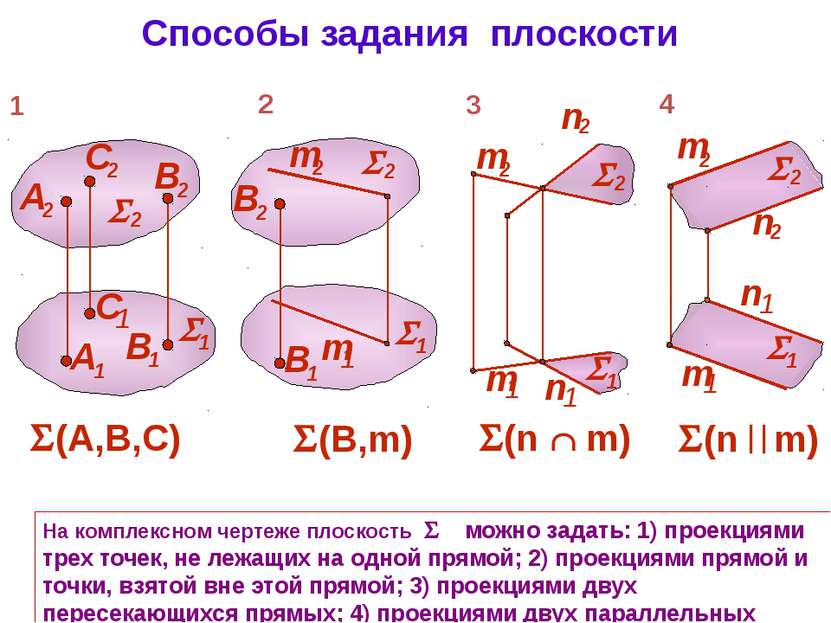
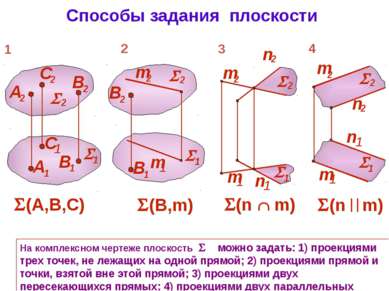Способы задания плоскости На комплексном чертеже плоскость можно задать: 1) проекциями трех точек, не лежащих на одной прямой; 2) проекциями прямой и точки, взятой вне этой прямой; 3) проекциями двух пересекающихся прямых; 4) проекциями двух параллельных прямых; (В,m) 2 (n m) 4 1
Cлайд 3
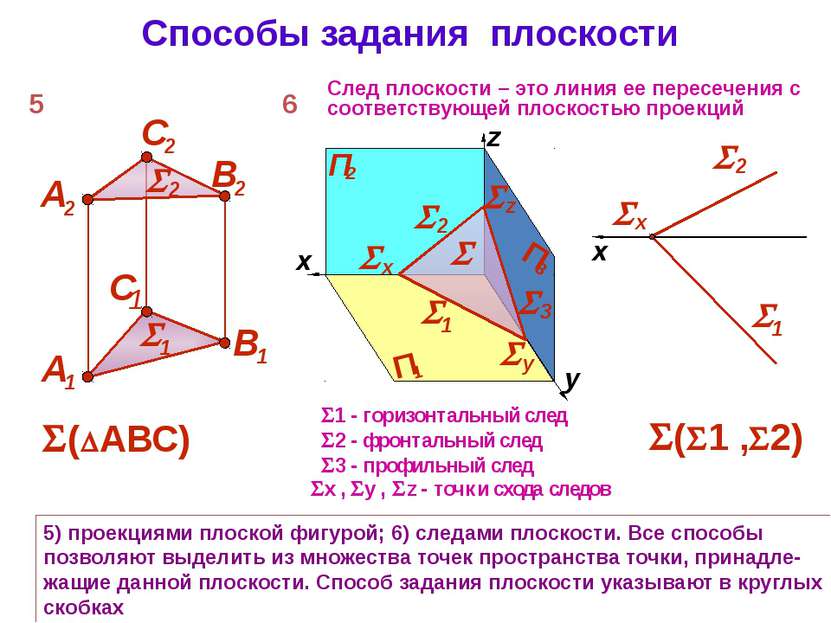
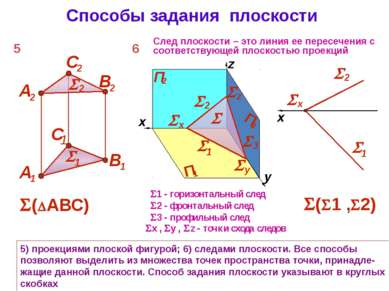Способы задания плоскости 5) проекциями плоской фигурой; 6) следами плоскости. Все способы позволяют выделить из множества точек пространства точки, принадле-жащие данной плоскости. Способ задания плоскости указывают в круглых скобках След плоскости – это линия ее пересечения с соответствующей плоскостью проекций 5 ( АВС) ( 1 , 2) x , y , z - точки схода следов
Cлайд 4
Положение плоскости относительно плоскостей проекций Плоскость общего положения наклонена ко всем плоскостям проекций Плоскость частного положения перпендикулярна или параллельна одной из плоскостей проекций Горизонтально проецирующая плоскость П1 Фронтально проецирующая плоскость П2 Профильно проецирующая плоскость П3 Горизонтальная плоскость П1 Фронтальная плоскость П2 Профильная плоскость П3 Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью: Плоскость, параллельная плоскости проекций, назы-вается плоскостью уровня (дважды проецирующей):
Cлайд 5
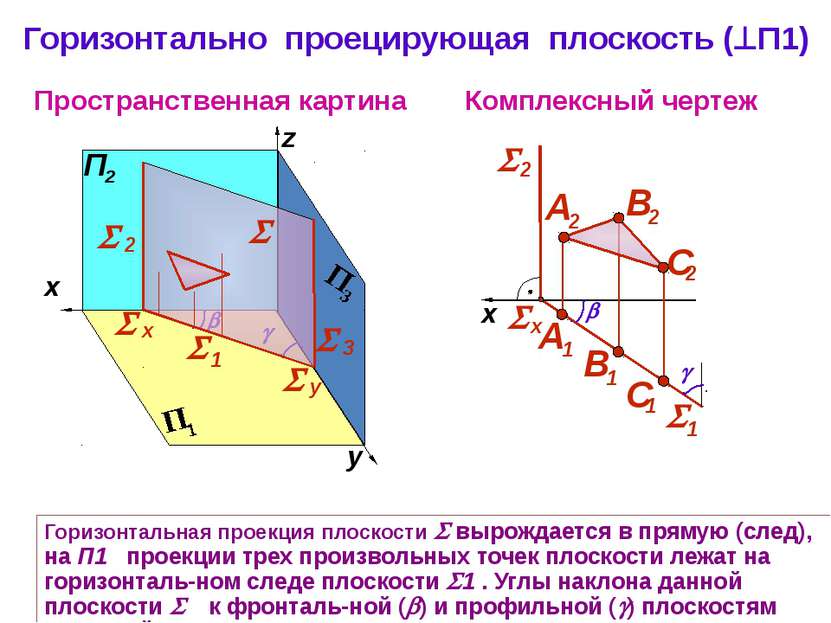
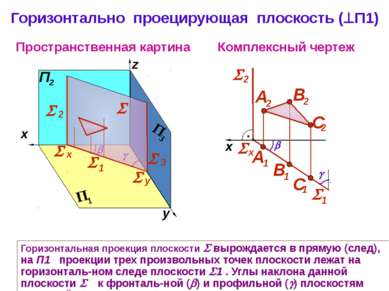Горизонтально проецирующая плоскость ( П1) Пространственная картина Комплексный чертеж y z Горизонтальная проекция плоскости вырождается в прямую (след), на П1 проекции трех произвольных точек плоскости лежат на горизонталь-ном следе плоскости 1 . Углы наклона данной плоскости к фронталь-ной ( ) и профильной ( ) плоскостям проекций на П1 не искажаются 3 1 2 х y
Cлайд 6
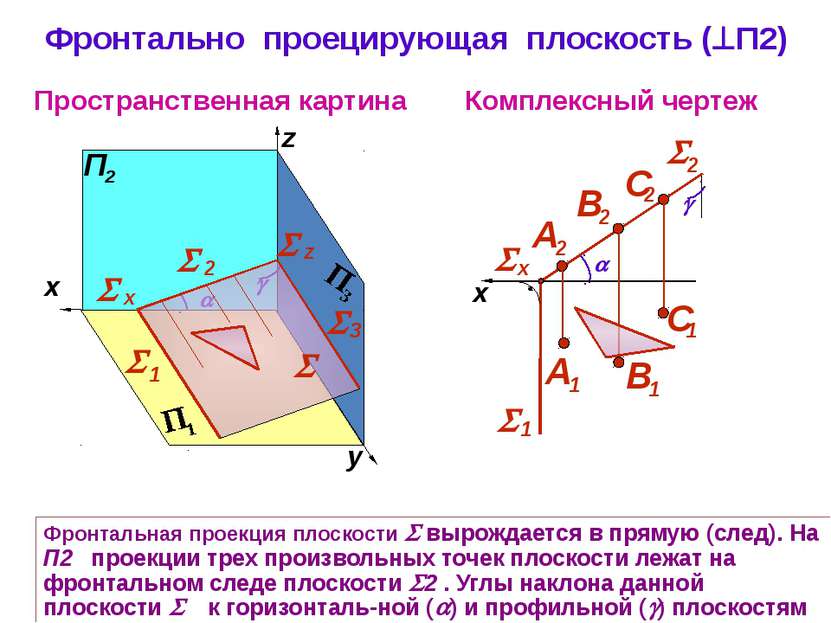
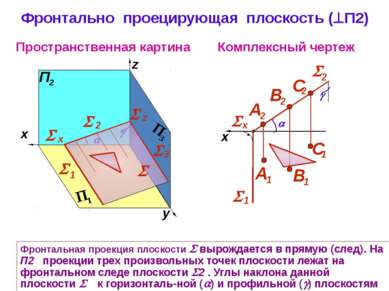Фронтально проецирующая плоскость ( П2) Комплексный чертеж y z Пространственная картина Фронтальная проекция плоскости вырождается в прямую (след). На П2 проекции трех произвольных точек плоскости лежат на фронтальном следе плоскости 2 . Углы наклона данной плоскости к горизонталь-ной ( ) и профильной ( ) плоскостям проекций на П2 не искажаются 1 х 2 z 3
Cлайд 7
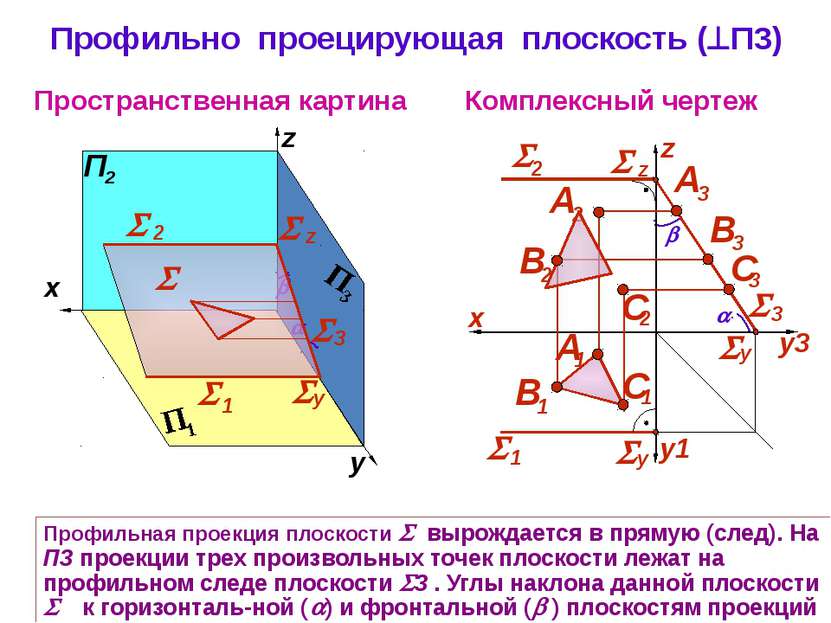
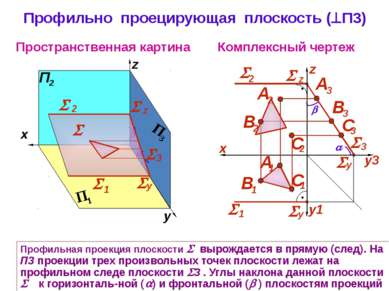Профильно проецирующая плоскость ( П3) Комплексный чертеж z Пространственная картина Профильная проекция плоскости вырождается в прямую (след). На П3 проекции трех произвольных точек плоскости лежат на профильном следе плоскости 3 . Углы наклона данной плоскости к горизонталь-ной ( ) и фронтальной ( ) плоскостям проекций на П3 не искажаются y z 3 1 y 2
Cлайд 8
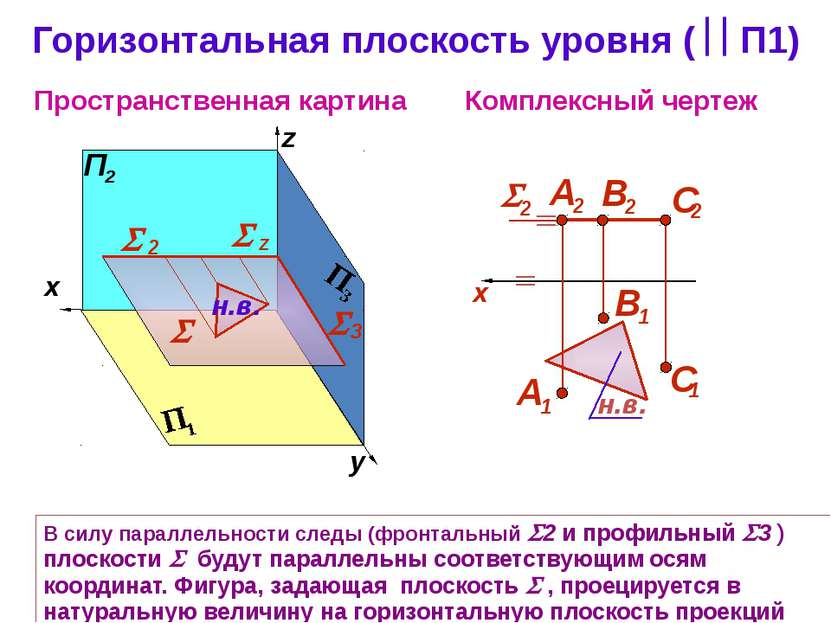
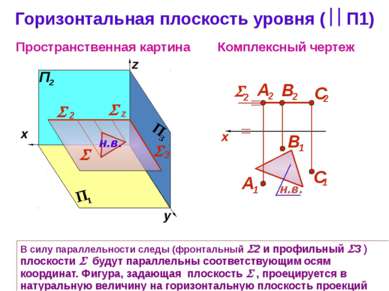Горизонтальная плоскость уровня ( П1) Комплексный чертеж z Пространственная картина В силу параллельности следы (фронтальный 2 и профильный 3 ) плоскости будут параллельны соответствующим осям координат. Фигура, задающая плоскость , проецируется в натуральную величину на горизонтальную плоскость проекций y z 3 2 н.в. x н.в.
Cлайд 9
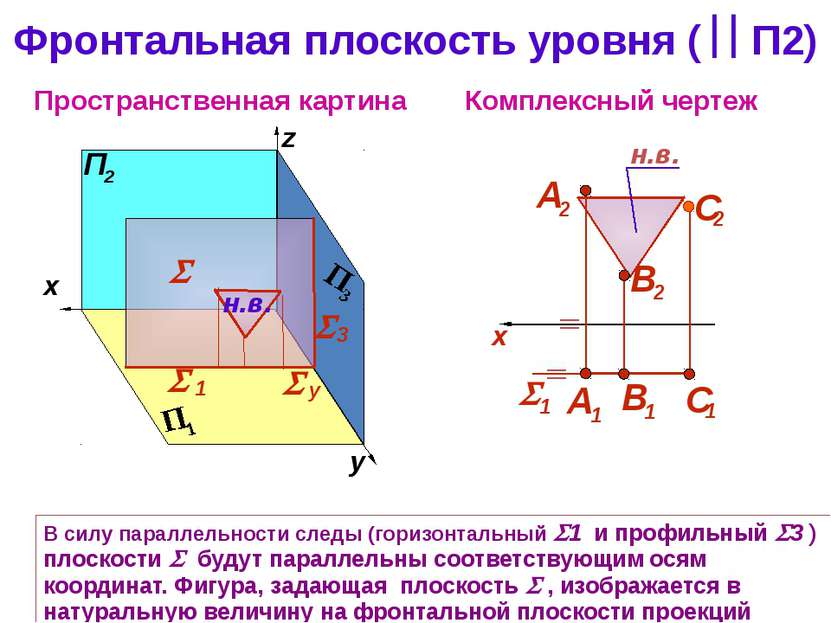
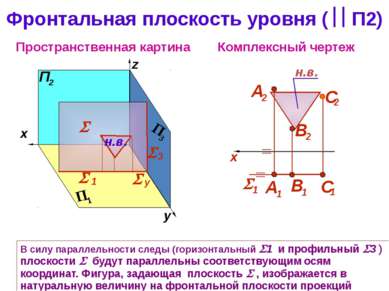Фронтальная плоскость уровня ( П2) Комплексный чертеж z Пространственная картина В силу параллельности следы (горизонтальный 1 и профильный 3 ) плоскости будут параллельны соответствующим осям координат. Фигура, задающая плоскость , изображается в натуральную величину на фронтальной плоскости проекций y y 3 1 н.в. н.в.
Cлайд 10
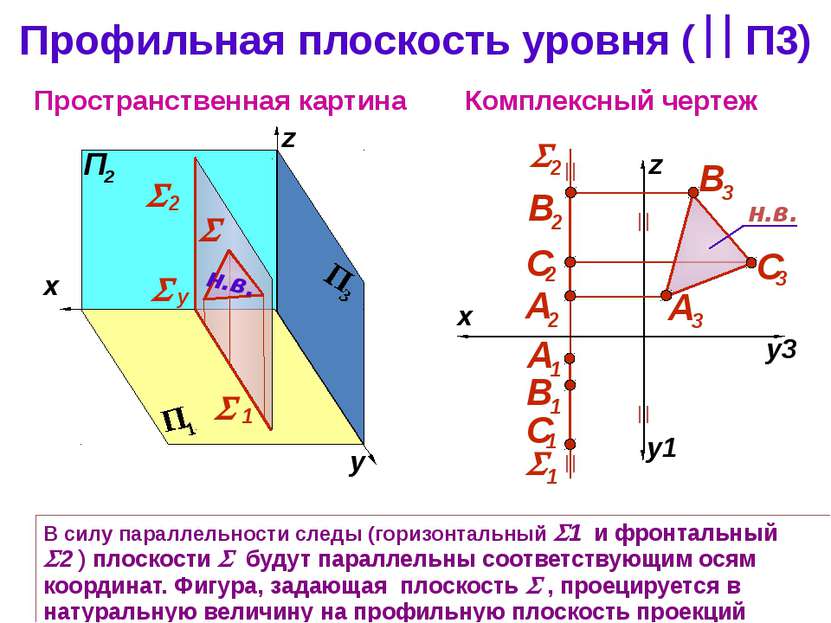
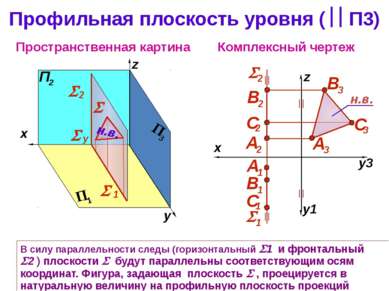Профильная плоскость уровня ( П3) Комплексный чертеж z Пространственная картина В силу параллельности следы (горизонтальный 1 и фронтальный 2 ) плоскости будут параллельны соответствующим осям координат. Фигура, задающая плоскость , проецируется в натуральную величину на профильную плоскость проекций y y 2 1 н.в. x y1 y3 z н.в.
Cлайд 11
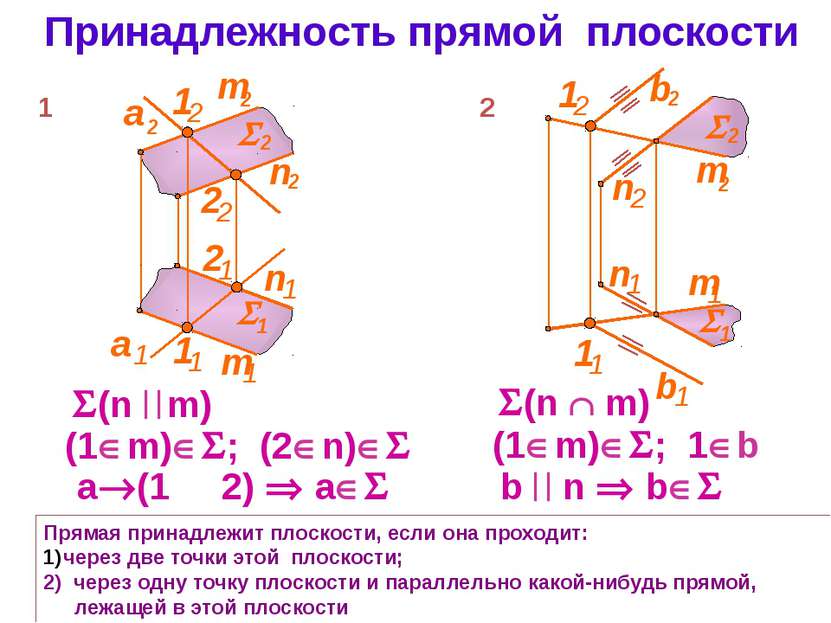
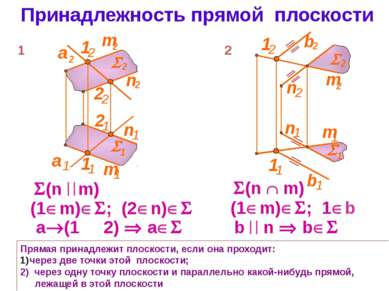Принадлежность прямой плоскости Прямая принадлежит плоскости, если она проходит: через две точки этой плоскости; 2) через одну точку плоскости и параллельно какой-нибудь прямой, лежащей в этой плоскости (n m) 1 (1 m) ; (2 n) а (1 И 2) а 2 (n m) (1 m) ; 1 b b n b m 2 m 1 m 2 2 1 n 1 n 2
Cлайд 12
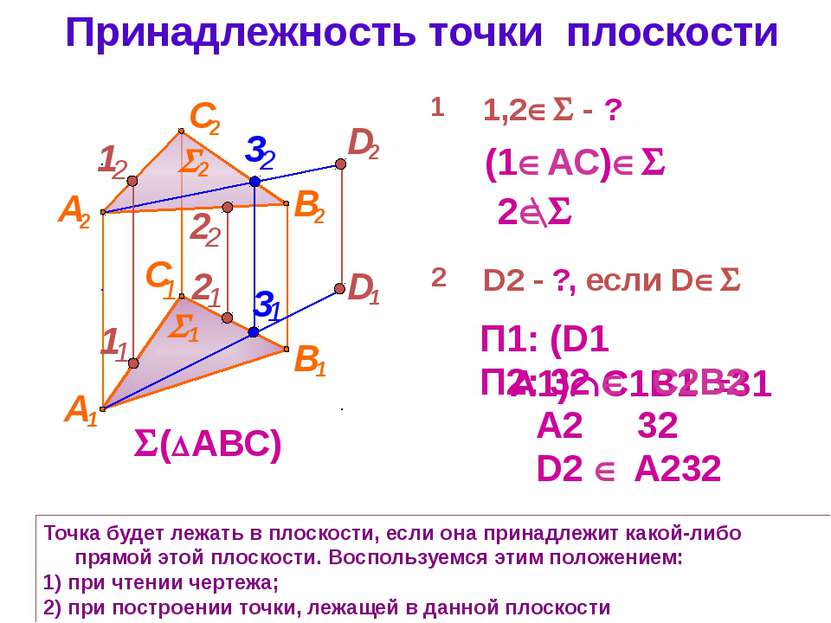
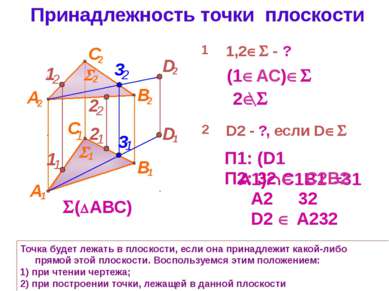Принадлежность точки плоскости Точка будет лежать в плоскости, если она принадлежит какой-либо прямой этой плоскости. Воспользуемся этим положением: 1) при чтении чертежа; 2) при построении точки, лежащей в данной плоскости (1 АС) П1: (D1 ИA1) С1В1 =31 ( АВС) 1 П2: 32 C2B2 1,2 - ? А2 И 32 D2 А232 А 2 С 1 С 2 В 2 В 1 1 2 2 2 D2 - ?, если D А 1
Cлайд 13
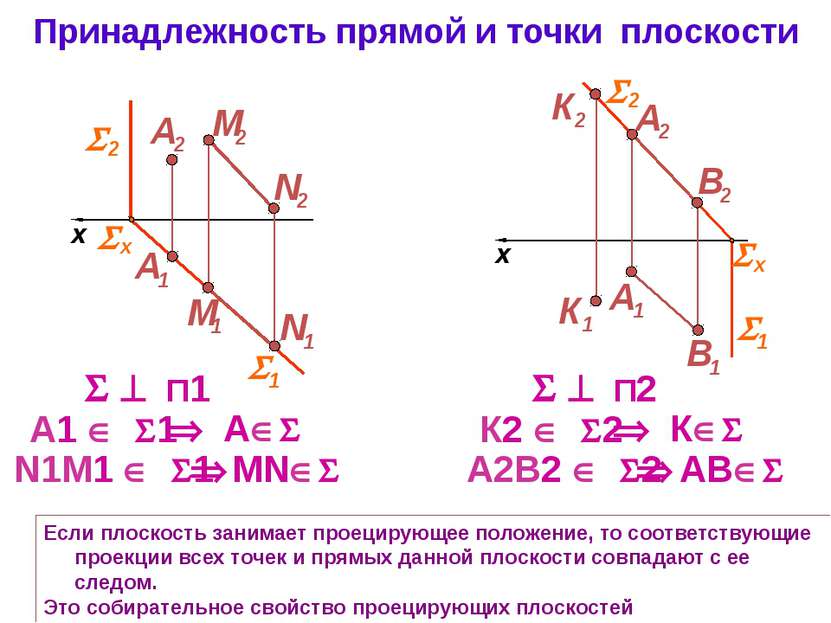
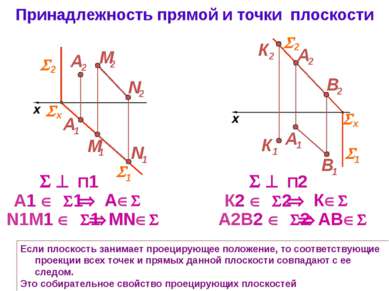Принадлежность прямой и точки плоскости Если плоскость занимает проецирующее положение, то соответствующие проекции всех точек и прямых данной плоскости совпадают с ее следом. Это собирательное свойство проецирующих плоскостей П1 x П2 x 1 2 х A1 1 А MN N1M1 1 1 2 х К2 2 К АВ А2В2 2
Cлайд 14
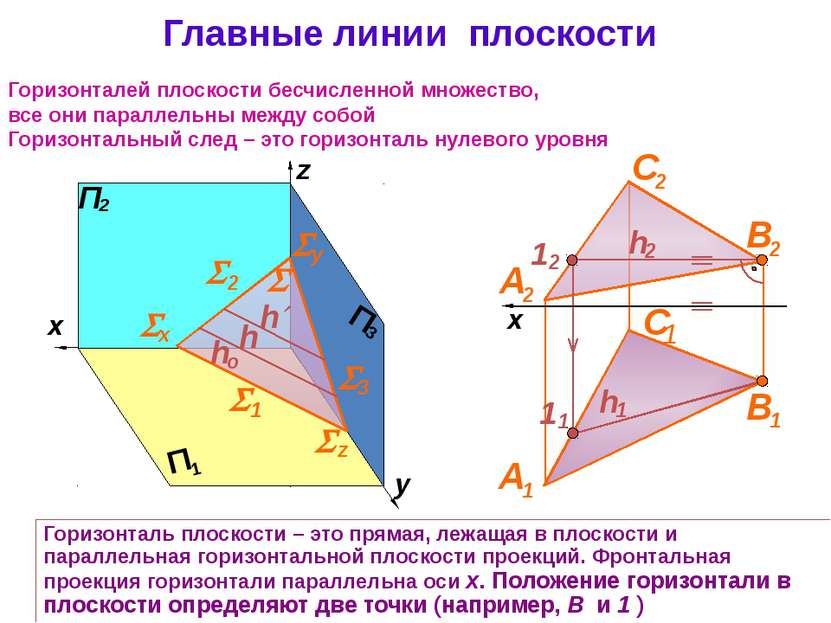
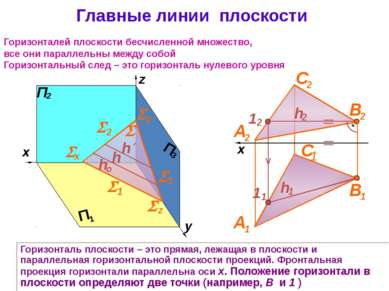Главные линии плоскости Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций. Фронтальная проекция горизонтали параллельна оси x. Положение горизонтали в плоскости определяют две точки (например, В и 1 ) Горизонталей плоскости бесчисленной множество, все они параллельны между собой Горизонтальный след – это горизонталь нулевого уровня x z y 1 2 3 х y z h А 2 В 2 С 2 А 1 В 1 С 1
Cлайд 15
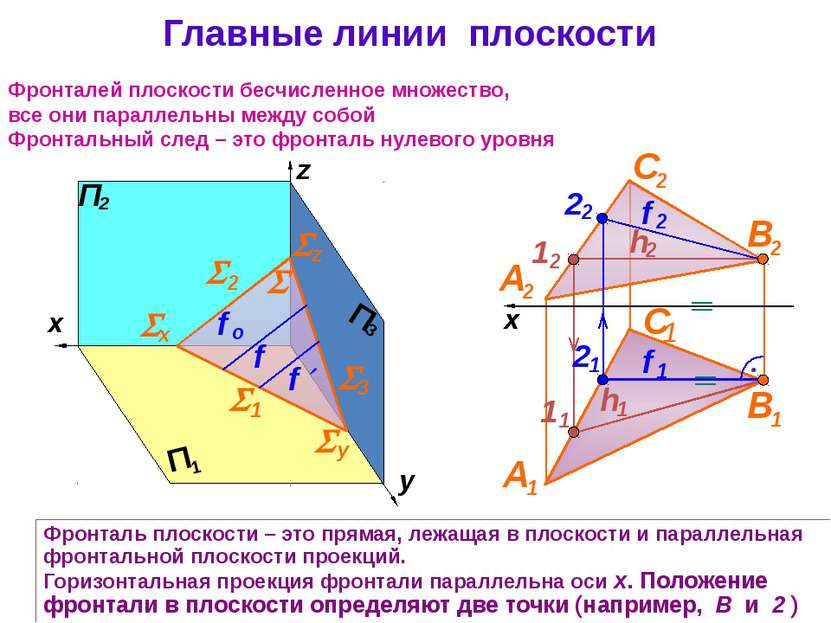
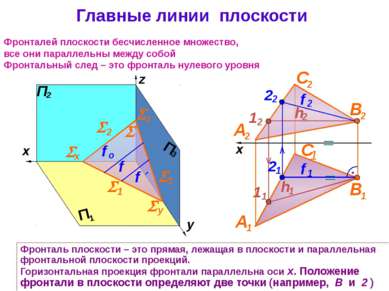Главные линии плоскости Фронталей плоскости бесчисленное множество, все они параллельны между собой Фронтальный след – это фронталь нулевого уровня Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали параллельна оси x. Положение фронтали в плоскости определяют две точки (например, В и 2 ) x z y 1 2 3 х z y f А 2 В 2 С 2 В 1 С 1 h 1 h 2 1 2 1 1 А 1
Cлайд 16
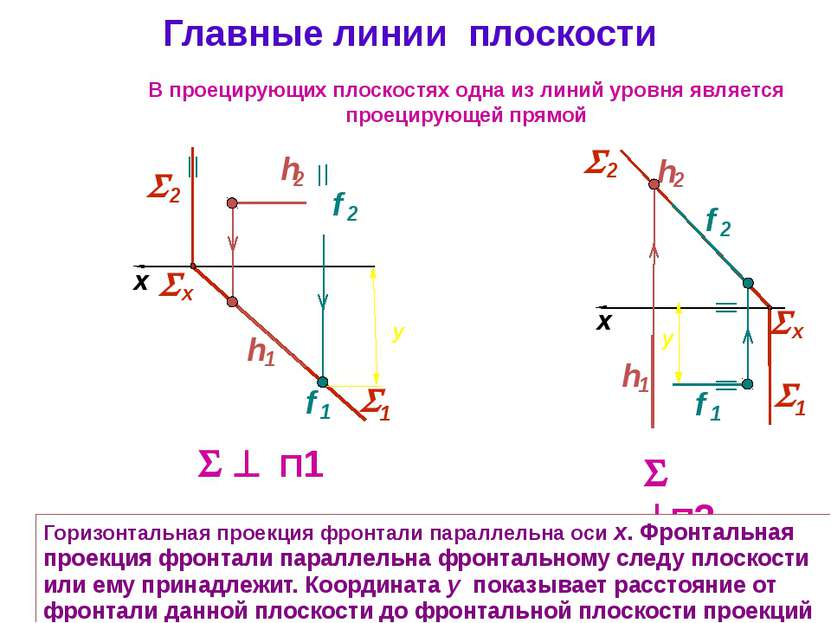
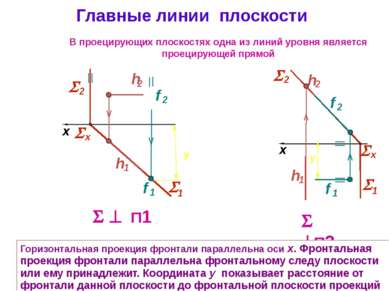Главные линии плоскости П1 x П2 x В проецирующих плоскостях одна из линий уровня является проецирующей прямой Горизонтальная проекция фронтали параллельна оси x. Фронтальная проекция фронтали параллельна фронтальному следу плоскости или ему принадлежит. Координата y показывает расстояние от фронтали данной плоскости до фронтальной плоскости проекций 1 2 х 1 2 х
Cлайд 17
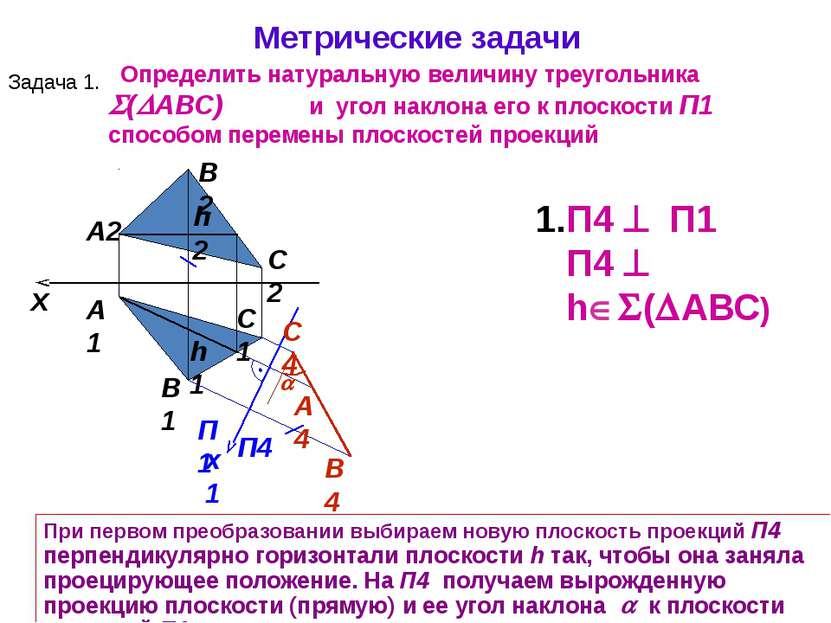
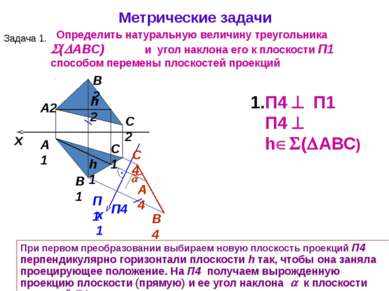А1 А2 При первом преобразовании выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h так, чтобы она заняла проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и ее угол наклона к плоскости проекций П1 . Определить натуральную величину треугольника ( АВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций B1 C2 B2 C1 x П4 П1 П4 h ( АВС) Метрические задачи Задача 1. h2 П1 П4 x1 h1 А4 В4 C4
Cлайд 18
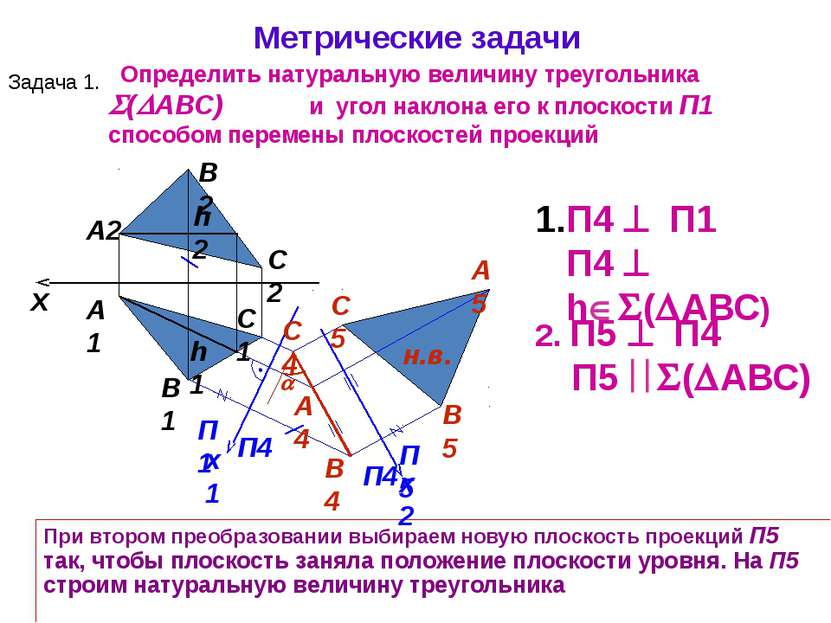
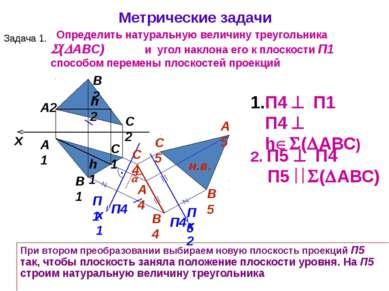x А1 А2 П1 П4 x1 П4 П1 П4 h ( АВС) 2. П5 П4 П5 ( АВС) При втором преобразовании выбираем новую плоскость проекций П5 так, чтобы плоскость заняла положение плоскости уровня. На П5 строим натуральную величину треугольника h1 h2 B1 C2 B2 А4 C1 В4 C4 Метрические задачи Задача 1. Определить натуральную величину треугольника ( АВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций н.в. C5 А5 В5
Cлайд 19
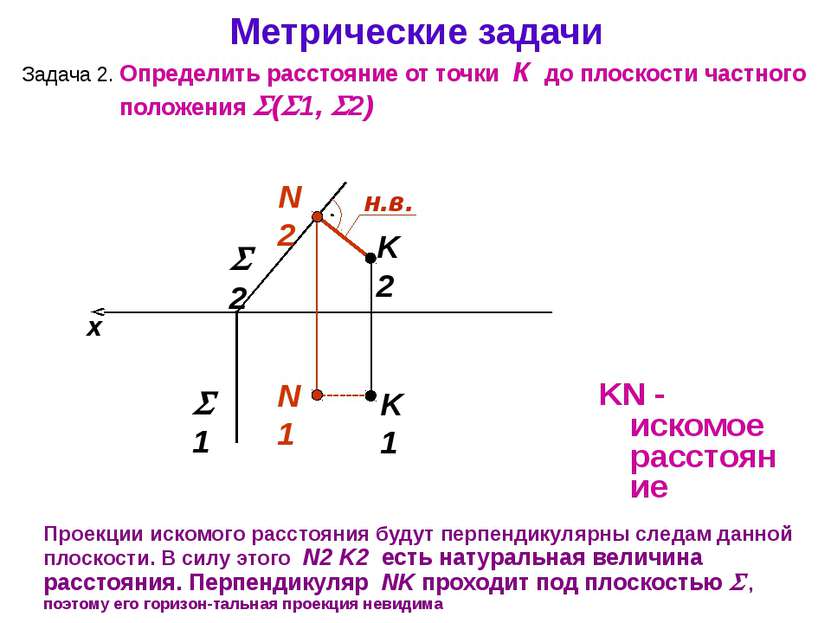
Метрические задачи Задача 2. Определить расстояние от точки К до плоскости частного положения ( 1, 2) x Проекции искомого расстояния будут перпендикулярны следам данной плоскости. В силу этого N2 K2 есть натуральная величина расстояния. Перпендикуляр NK проходит под плоскостью , поэтому его горизон-тальная проекция невидима 2 K1 1 K2 KN - искомое расстояние N1 н.в.
Cлайд 20
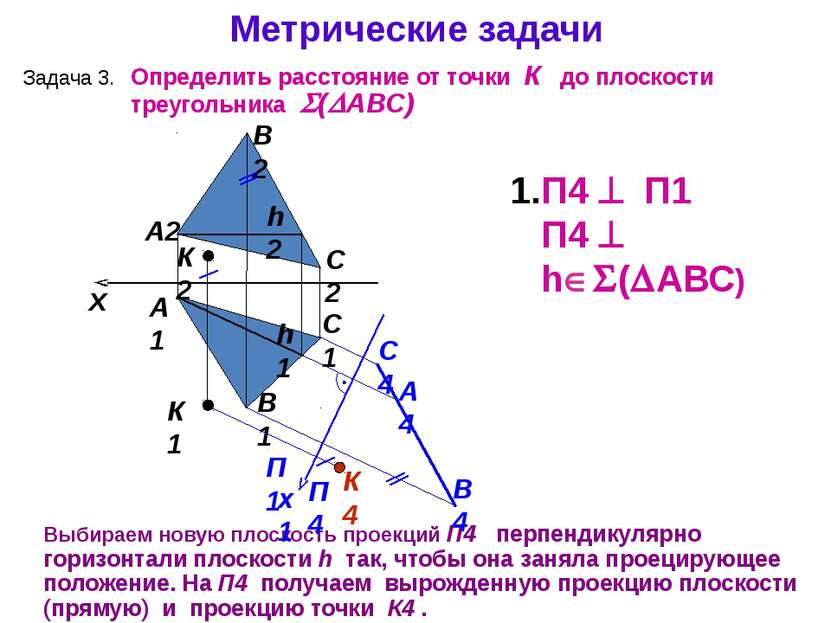
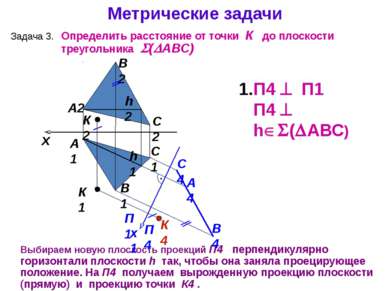Метрические задачи А1 А2 Выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h так, чтобы она заняла проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и проекцию точки К4 . Задача 3. B1 C2 B2 C1 x П4 П1 П4 h ( АВС) К1 К2 Определить расстояние от точки К до плоскости треугольника ( АВС) h2 П1 П4 x1 h1 А4 В4 C4 К4
Cлайд 21
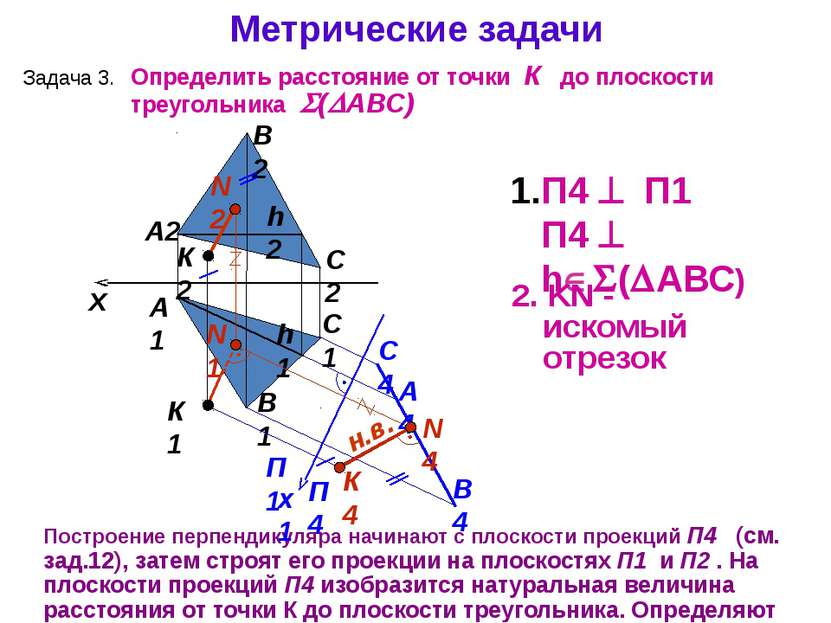
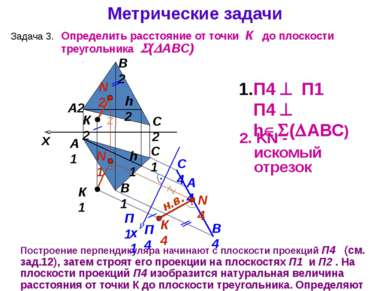А1 А2 Построение перпендикуляра начинают с плоскости проекций П4 (см. зад.12), затем строят его проекции на плоскостях П1 и П2 . На плоскости проекций П4 изобразится натуральная величина расстояния от точки К до плоскости треугольника. Определяют видимость перпендикуляра. B1 C2 B2 C1 x П4 П1 П4 h ( АВС) 2. KN - искомый отрезок К1 К2 Метрические задачи Задача 3. Определить расстояние от точки К до плоскости треугольника ( АВС) h2 П1 П4 x1 h1 N2 А4 В4 C4 N1 н.в. К4
