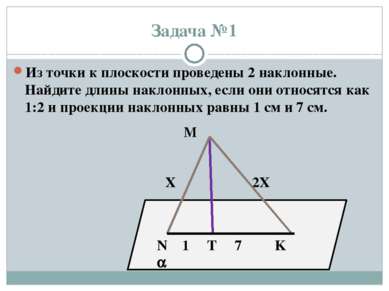
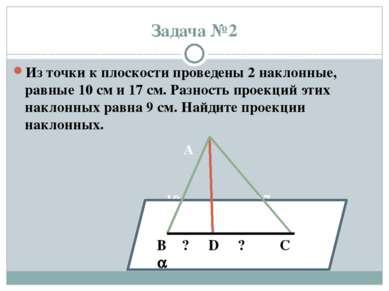
X
Код презентации скопируйте его
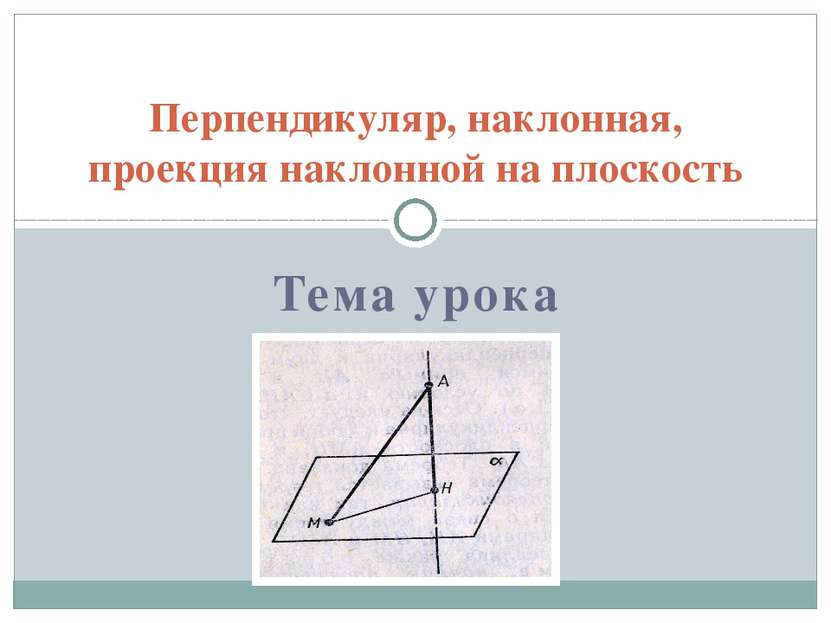
Перпендикуляр, наклонная, проекция наклонной на плоскость
Скачать эту презентацию
Презентация на тему Перпендикуляр, наклонная, проекция наклонной на плоскость
Скачать эту презентациюCлайд 1
Тема урока Перпендикуляр, наклонная, проекция наклонной на плоскость
Cлайд 2
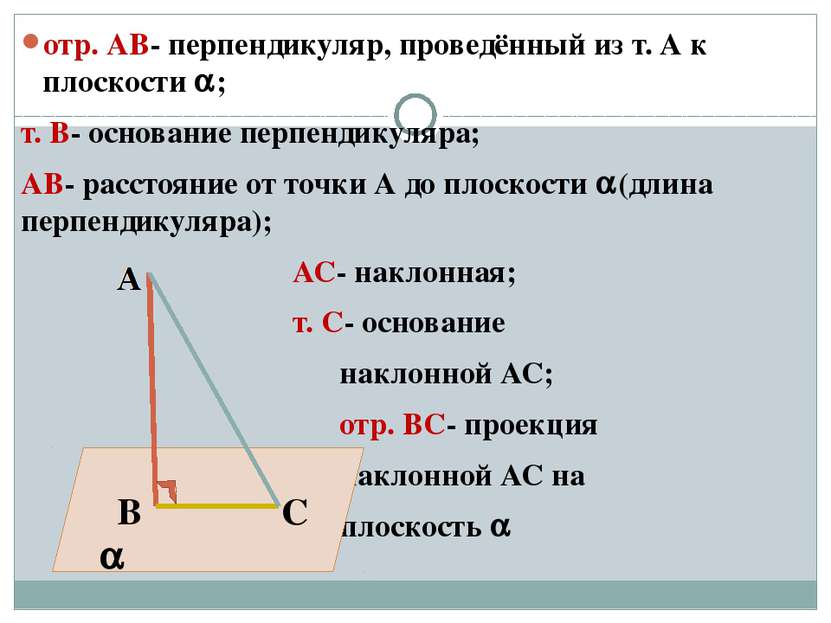
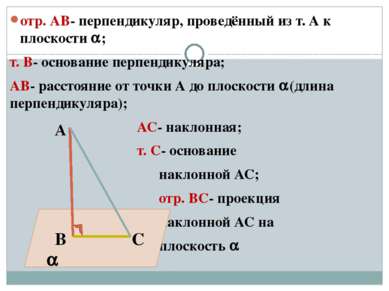отр. АВ- перпендикуляр, проведённый из т. А к плоскости ; т. В- основание перпендикуляра; АВ- расстояние от точки А до плоскости (длина перпендикуляра); АС- наклонная; т. С- основание наклонной АС; отр. ВС- проекция наклонной АС на плоскость В С
Cлайд 3
Определение 1 Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащих на прямой, перпендикулярной плоскости.
Cлайд 4
Определение 2 Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Определение 3 Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Cлайд 5
Определение 4 Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости и не являющийся перпендикуляром к плоскости.
Cлайд 6
Определение 5 Конец отрезка, лежащий в плоскости, называется основанием наклонной. Определение 6 Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.
Cлайд 7
Наглядное представление перпендикуляра
Cлайд 8
Задача №1 Из точки к плоскости проведены 2 наклонные. Найдите длины наклонных, если они относятся как 1:2 и проекции наклонных равны 1 см и 7 см. М Х 2Х N 1 T 7 K
Cлайд 9
Задача №2 Из точки к плоскости проведены 2 наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найдите проекции наклонных. A 10 17 В ? D ? C
