X
Код презентации скопируйте его
Четырехугольники
Скачать эту презентацию
Презентация на тему Четырехугольники
Скачать эту презентациюCлайд 1
Четырехугольники Выполнила ученица 8а класса Велумян Люсине, учитель – Гончаров О. Н. МОУ «Верхопенская средняя общеобразовательная школа имени М. Р. Абросимова»
Cлайд 2
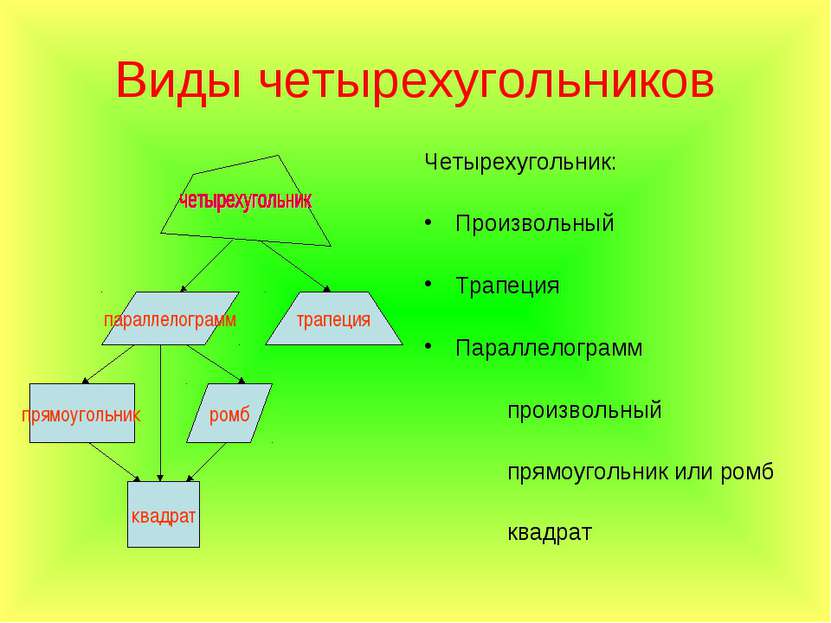
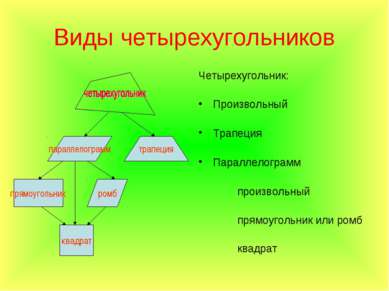Виды четырехугольников Четырехугольник: Произвольный Трапеция Параллелограмм произвольный прямоугольник или ромб квадрат
Cлайд 3
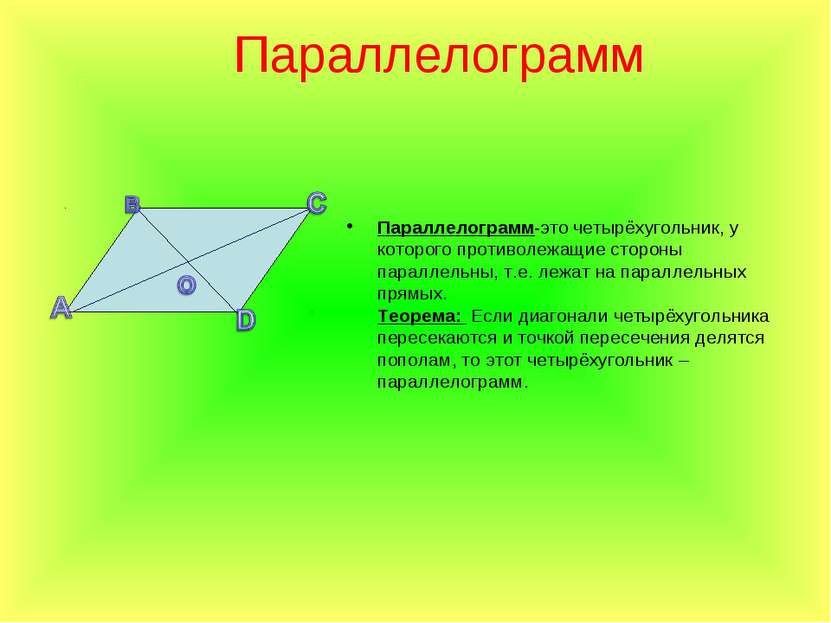
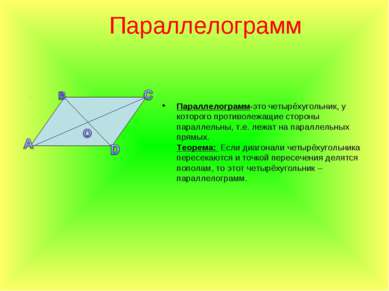Параллелограмм Параллелограмм-это четырёхугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых. Теорема: Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник –параллелограмм.
Cлайд 4
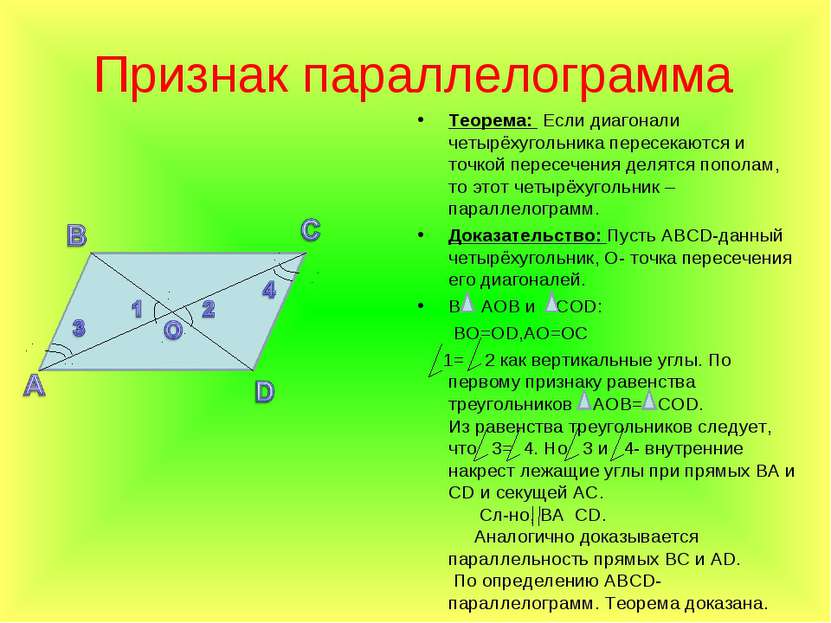
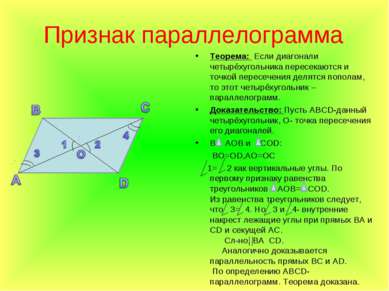Признак параллелограмма Теорема: Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник –параллелограмм. Доказательство: Пусть АВСD-данный четырёхугольник, О- точка пересечения его диагоналей. В АОВ и СОD: BO=OD,AO=OС 1= 2 как вертикальные углы. По первому признаку равенства треугольников AOB= COD. Из равенства треугольников следует, что 3= 4. Но 3 и 4- внутренние накрест лежащие углы при прямых ВА и СD и секущей АС. Сл-но, ВА CD. Аналогично доказывается параллельность прямых ВС и АD. По определению АВСD-параллелограмм. Теорема доказана.
Cлайд 5
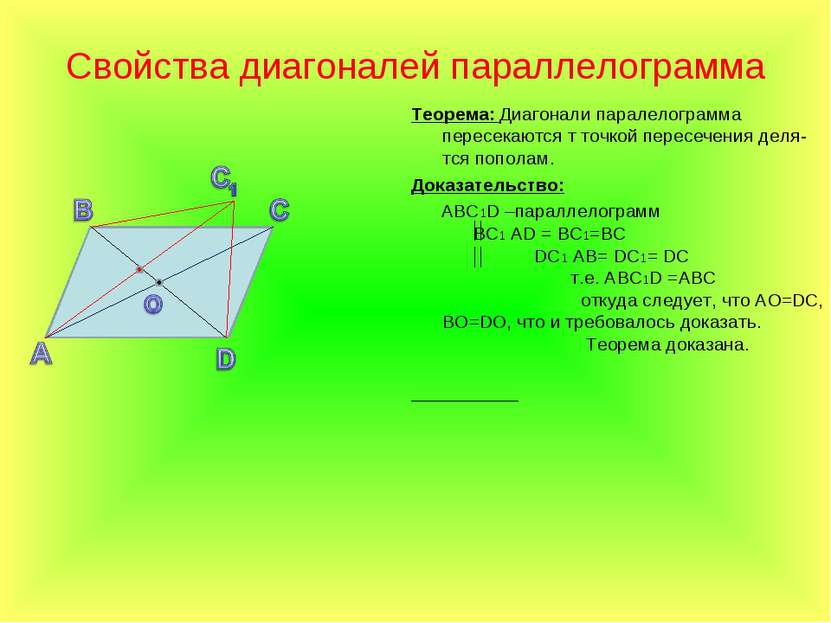
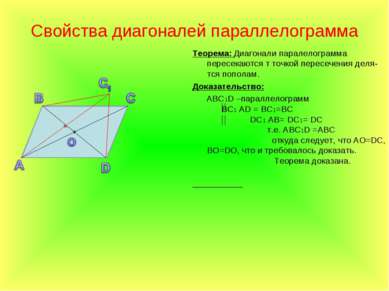Свойства диагоналей параллелограмма Теорема: Диагонали паралелограмма пересекаются т точкой пересечения деля-тся пополам. Доказательство: АВС1D –параллелограмм ВС1 АD = BС1=BС DС1 АВ= DС1= DС т.е. АВС1D =АВС откуда следует, что АО=DС, ВО=DО, что и требовалось доказать. Теорема доказана.
Cлайд 6
ПРЯМОУГОЛЬНИК Определение: Прямоугольник- это параллелограмм, к которого все углы прямые. Теорема: Диагонали прямоугольника равны.
Cлайд 7
ПРИЗНАК ПРЯМОУГОЛЬНИКА Теорема: Диагонали прямоугольника равны. Доказательство: Пусть АВС D– данный прямоугольник. Утверждение теоремы следует из равенства прямоугольных треугольников ВАD и СD А. У них углы ВАD и СDА прямые. Катет АD общий, А катеты АВ и СD равны как противолежащие стороны параллелограмма. Из равенства треугольников следует, что их гипотенузы равны. А гипотенузы есть диагонали прямоугольника. Теорема доказана.
Cлайд 8
РОМБ Определение: Ромб- это параллелограмм, у которого все стороны равны. Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисой его углов.
Cлайд 9
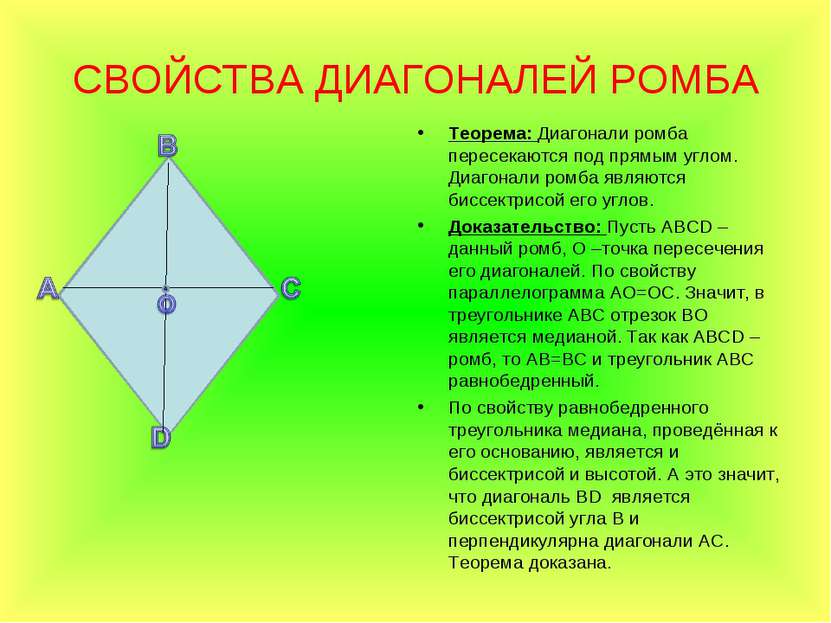
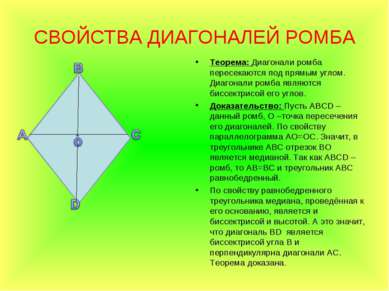СВОЙСТВА ДИАГОНАЛЕЙ РОМБА Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисой его углов. Доказательство: Пусть АВСD – данный ромб, О –точка пересечения его диагоналей. По свойству параллелограмма АО=ОС. Значит, в треугольнике АВС отрезок ВО является медианой. Так как АВСD – ромб, то АВ=ВС и треугольник АВС равнобедренный. По свойству равнобедренного треугольника медиана, проведённая к его основанию, является и биссектрисой и высотой. А это значит, что диагональ ВD является биссектрисой угла В и перпендикулярна диагонали АС. Теорема доказана.
Cлайд 10
КВАДРАТ Квадрат-это прямоугольник, у которого все стороны равны. Так как стороны квадрата равны, то он является также ромбом. Поэтому квадрат обладает свойствами прямоугольника и ромба: 1.У квадрата все углы прямые. 2.Диагонали квадрата равны. 3. Диагонали квадрата пересекаются под прямым углом, и являются биссектрисами его углов.
