X
Код презентации скопируйте его
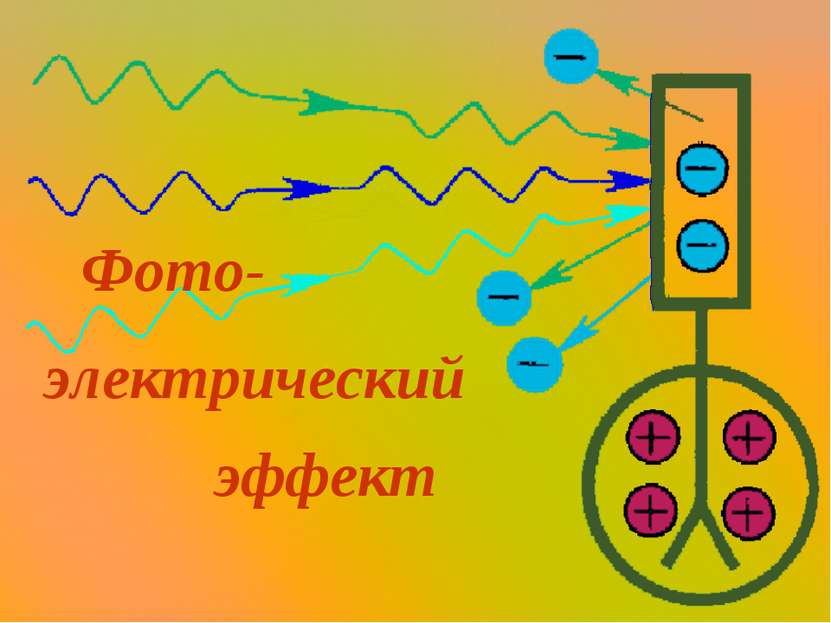
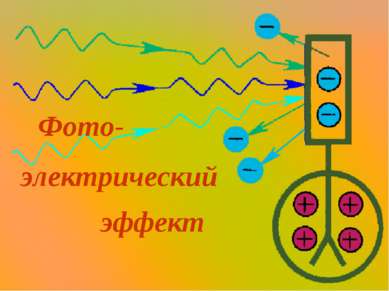
Фото-электрический эффект
Скачать эту презентацию
Презентация на тему Фото-электрический эффект
Скачать эту презентациюCлайд 1
Фото- электрический эффект
Cлайд 2
Открытие фотоэффекта Фотоэлектрический эффект был открыт в 1887 году немецким физиком и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Ленардом в 1900 г. Г. Герцем
Cлайд 3
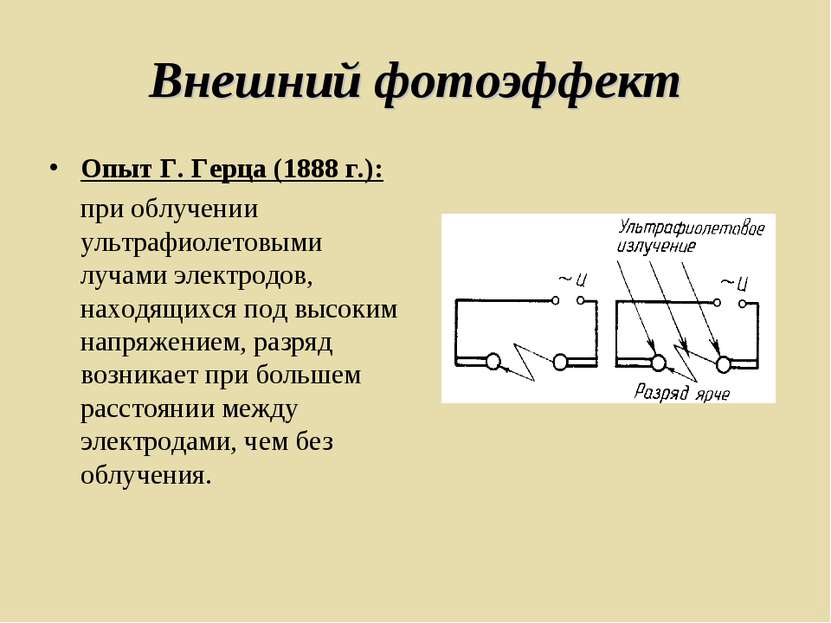
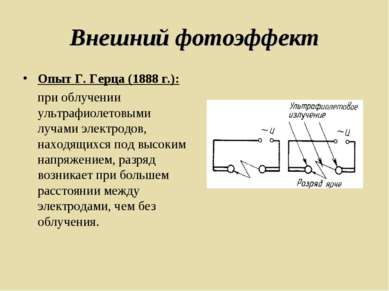Внешний фотоэффект Опыт Г. Герца (1888 г.): при облучении ультрафиолетовыми лучами электродов, находящихся под высоким напряжением, разряд возникает при большем расстоянии между электродами, чем без облучения.
Cлайд 4
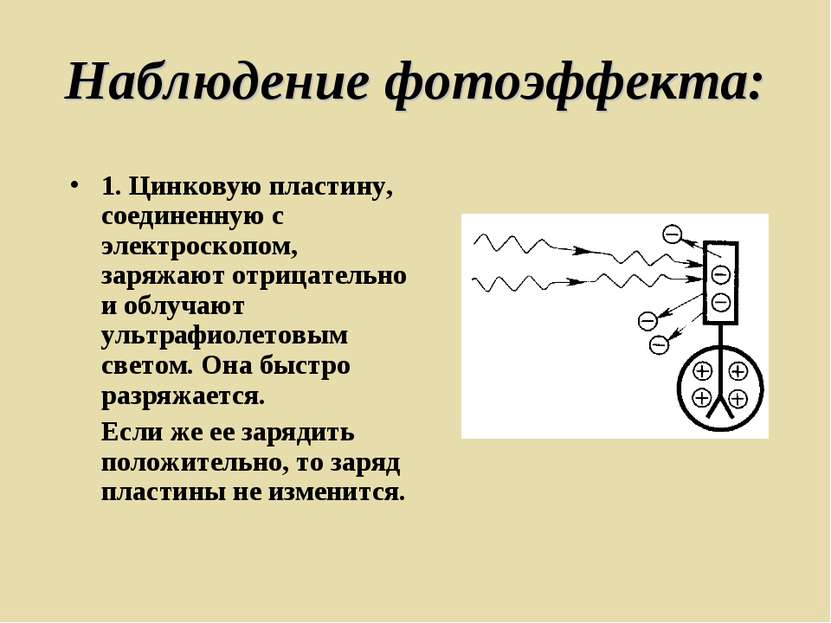
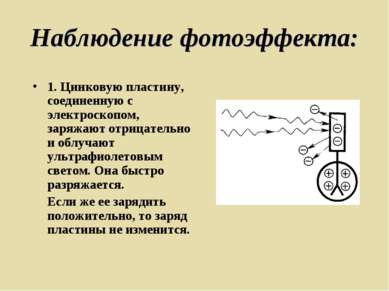Наблюдение фотоэффекта: 1. Цинковую пластину, соединенную с электроскопом, заряжают отрицательно и облучают ультрафиолетовым светом. Она быстро разряжается. Если же ее зарядить положительно, то заряд пластины не изменится.
Cлайд 5
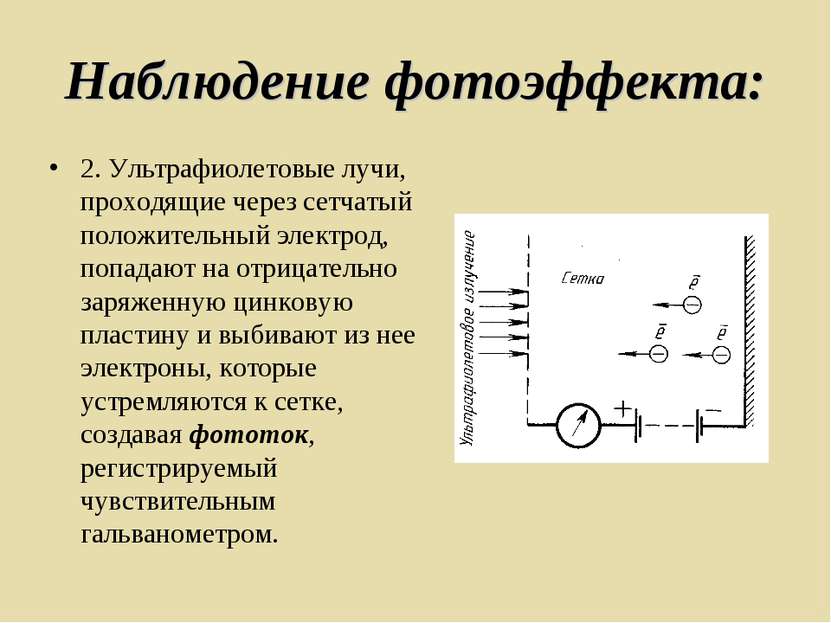
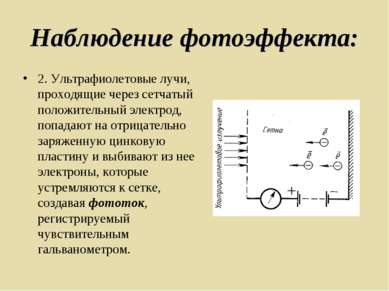Наблюдение фотоэффекта: 2. Ультрафиолетовые лучи, проходящие через сетчатый положительный электрод, попадают на отрицательно заряженную цинковую пластину и выбивают из нее электроны, которые устремляются к сетке, создавая фототок, регистрируемый чувствительным гальванометром.
Cлайд 6
Внешний фотоэффект Фотоэффект - явление испускания электронов с поверхности металла под действием света. Т.е. свет выбивает (вырывает) электроны из металла.
Cлайд 7
Столетов Александр Григорьевич (1839-1896) Русский физик, научные работы посвящены электромагнетизму, оптике, молекулярной физике, философским вопросам науки. Впервые показал, что при увеличении намагничивающего поля, магнитная восприимчивость железа сначала возрастает, а затем падает, проходя через максимум, осуществил ряд экспериментов для определения величины отношения электромагнитных и электростатических величин, получил значение, близкое к значению скорости света (1876г.). В 1888-90г. выполнил цикл работ по исследованию явления внешнего фотоэффекта, создал первый фотоэлемент (1888г.), является основоположником количественных методов исследования фотоэффекта, изучал несамостоятельный газовый разряд, исследовал критическое состояние вещества, многое сделал для развития физики в России. В 1872г создал первую физическую лабораторию и исследовательский институт при Московском университете. Количественные закономерности фотоэффекта были установлены А.Г.Столетовым (1888—1889).
Cлайд 8
Схема экспериментальной установки для изучения фотоэффекта.
Cлайд 9
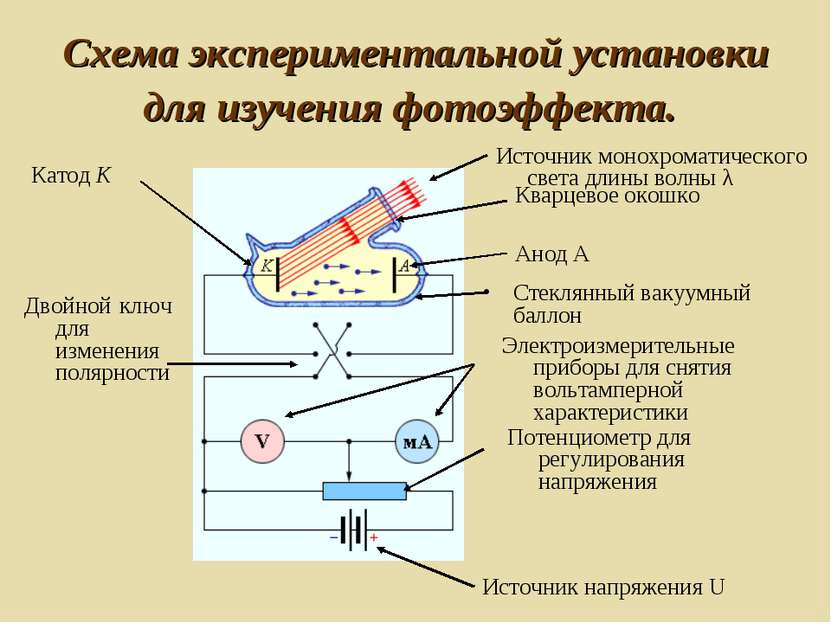
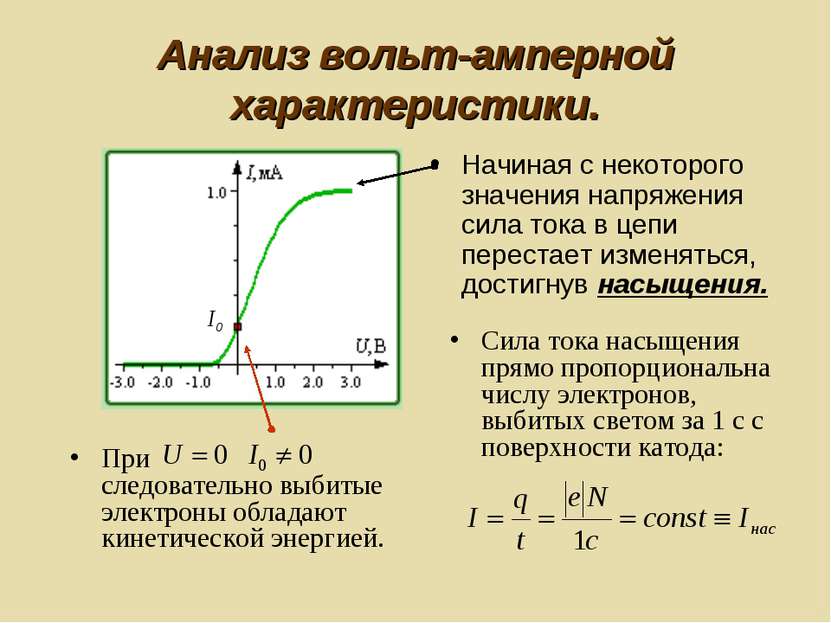
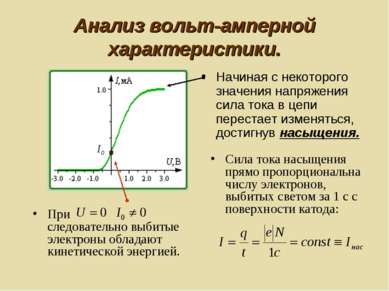Анализ вольт-амперной характеристики. Начиная с некоторого значения напряжения сила тока в цепи перестает изменяться, достигнув насыщения. При следовательно выбитые электроны обладают кинетической энергией. Сила тока насыщения прямо пропорциональна числу электронов, выбитых светом за 1 с с поверхности катода:
Cлайд 10
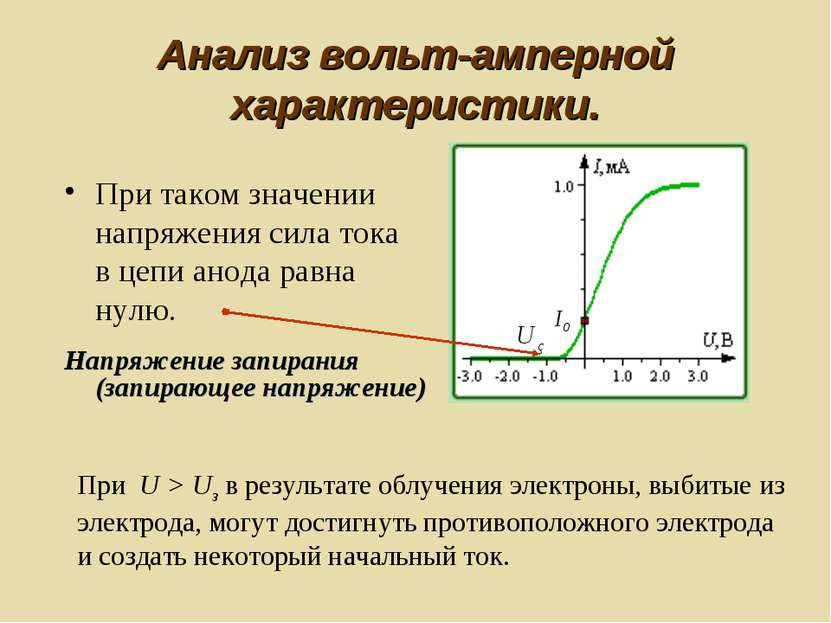
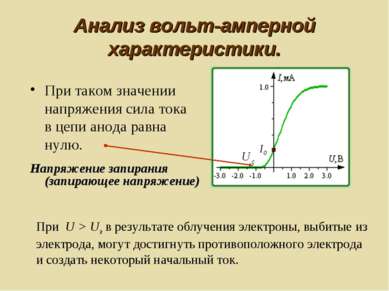Анализ вольт-амперной характеристики. При таком значении напряжения сила тока в цепи анода равна нулю. Напряжение запирания (запирающее напряжение) При U > Uз в результате облучения электроны, выбитые из электрода, могут достигнуть противоположного электрода и создать некоторый начальный ток.
Cлайд 11
Анализ вольт-амперной характеристики. Согласно закону сохранения энергии где m - масса электрона, а υmax - максимальная скорость фотоэлектрона.
Cлайд 12
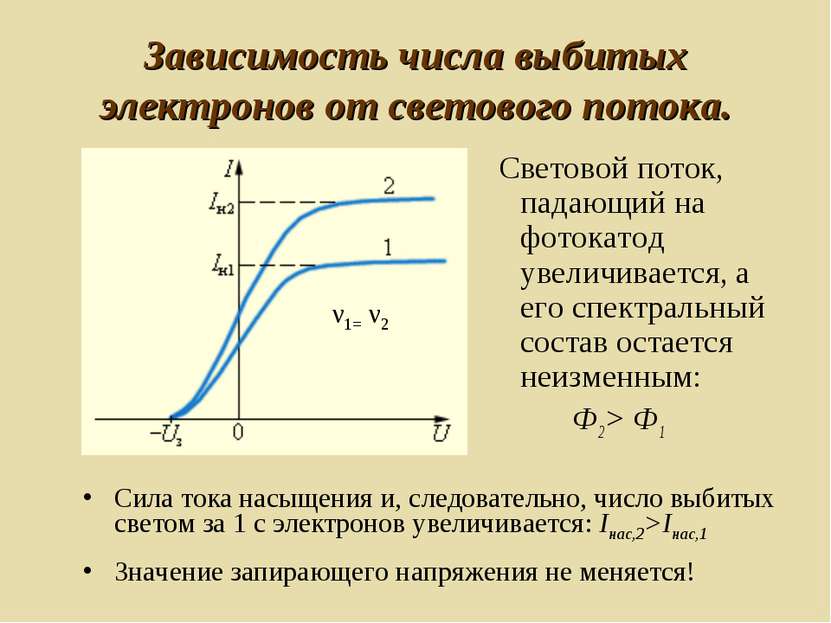
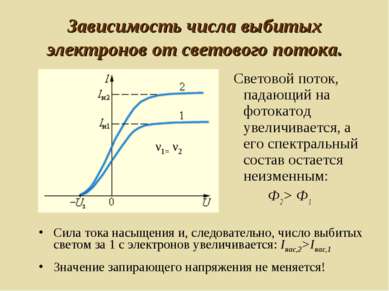Зависимость числа выбитых электронов от светового потока. Световой поток, падающий на фотокатод увеличивается, а его спектральный состав остается неизменным: Ф2 > Ф1 Сила тока насыщения и, следовательно, число выбитых светом за 1 с электронов увеличивается: Iнас,2>Iнас,1 Значение запирающего напряжения не меняется!
Cлайд 13
Первый закон фотоэффекта Фототок насыщения пропорционален световому потоку, падающему на металл. или Количество фотоэлектронов, выбиваемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны.
Cлайд 14
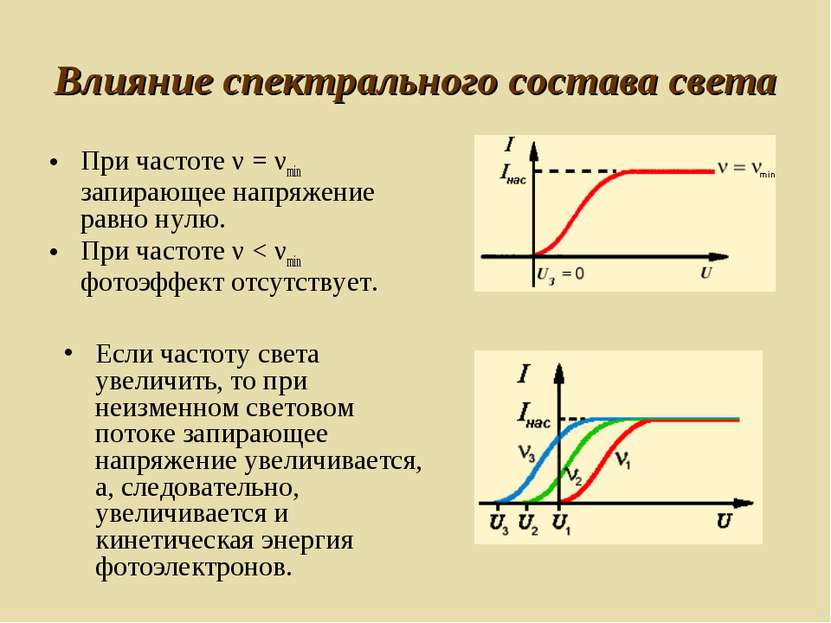
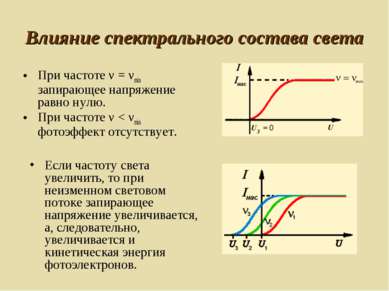Влияние спектрального состава света При частоте ν = νmin запирающее напряжение равно нулю. При частоте ν < νmin фотоэффект отсутствует. Если частоту света увеличить, то при неизменном световом потоке запирающее напряжение увеличивается, а, следовательно, увеличивается и кинетическая энергия фотоэлектронов.
Cлайд 15
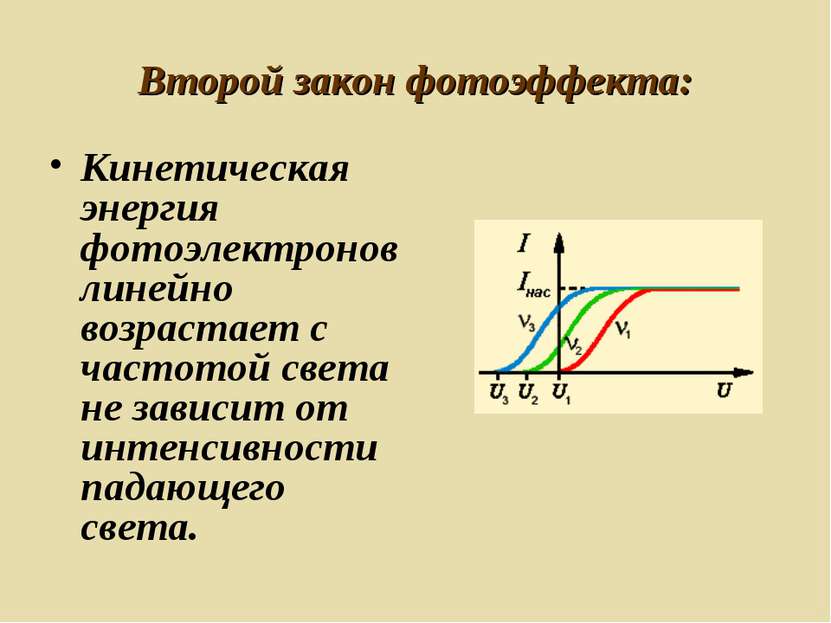
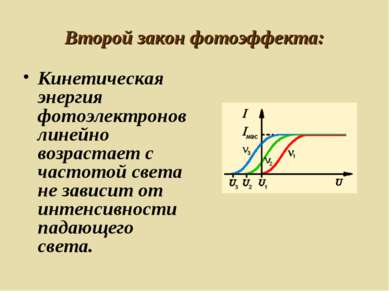Второй закон фотоэффекта: Кинетическая энергия фотоэлектронов линейно возрастает с частотой света не зависит от интенсивности падающего света.
Cлайд 16
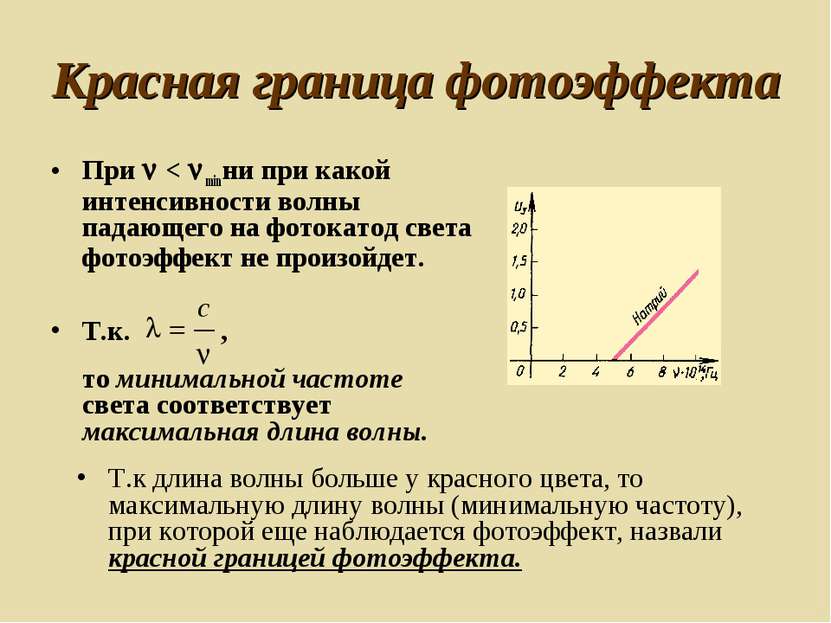
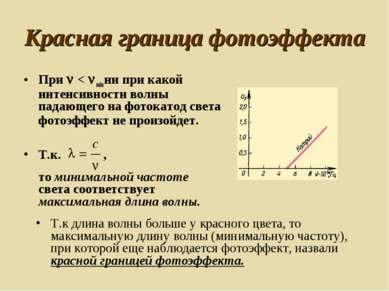Красная граница фотоэффекта При < min ни при какой интенсивности волны падающего на фотокатод света фотоэффект не произойдет. Т.к. , то минимальной частоте света соответствует максимальная длина волны. Т.к длина волны больше у красного цвета, то максимальную длину волны (минимальную частоту), при которой еще наблюдается фотоэффект, назвали красной границей фотоэффекта.
Cлайд 17
Третий закон фотоэффекта Заменяя в приборе материал фотокатода, Столетов установил, что красная граница фотоэффекта является характеристикой данного вещества. Для каждого вещества существует красная граница фотоэффекта, т. е. существует наименьшая частота min , при которой еще возможен фотоэффект.
Cлайд 18
Законы фотоэффекта: Количество фотоэлектронов, выбиваемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Кинетическая энергия фотоэлектронов линейно возрастает с частотой света не зависит от интенсивности падающего света. Для каждого вещества существует красная граница фотоэффекта, т. е. существует наименьшая частота min , при которой еще возможен фотоэффект. Фотоэффект практически безынерционен, фототок возникает мгновенно после начала освещения катода при условии, что частота света ν > νmin.
Cлайд 19
Что не могла объяснить волновая теория света: Безынерционность фотоэффекта. В волновой модели: электрон при взаимодействии с электромагнитной световой волной постепенно накапливает энергию, и только через значительное время вылетит из катода. Как показывают расчеты, это время должно было бы исчисляться минутами или часами. Существование красной границы фотоэффекта. В волновой модели: необходимую энергию можно накопить при любой энергии волны. Независимость энергии фотоэлектронов от интенсивности светового потока. Пропорциональность максимальной кинетической энергии частоте света.
Cлайд 20
Идея Эйнштейна (1905 г.) Свет имеет прерывистую дискретную структуру. Электромагнитная волна состоит из отдельных порций – квантов, впоследствии названных фотонами. Квант поглощается электроном целиком. Энергия кванта передается электрону. (Один фотон выбивает один электрон.) Энергия каждого фотона определяется формулой Планка W = E = hν, где h – постоянная Планка.
Cлайд 21
Уравнение Эйнштейна На основании закона сохранения энергии: Смысл уравнения Эйнштейна: энергия кванта тратится на работу выхода электрона из металла и сообщение электрону кинетической энергии. В этом уравнении: ν - частота падающего света, m - масса электрона (фотоэлектрона), υ - скорость электрона, h - постоянная Планка, A - работа выхода электронов из металла.
Cлайд 22
Работа выхода Она показывает, какую работу должен совершить электрон, чтобы преодолеть поверхностную разность потенциалов и выйти за пределы металла. Работа выхода обычно измеряется в электронвольтах (эВ).
Cлайд 23
Доказательство законов фотоэффекта Число фотонов Nф равно числу электронов Nэ. Энергия монохроматического света Следовательно, Количество фотоэлектронов, выбиваемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны.
Cлайд 24
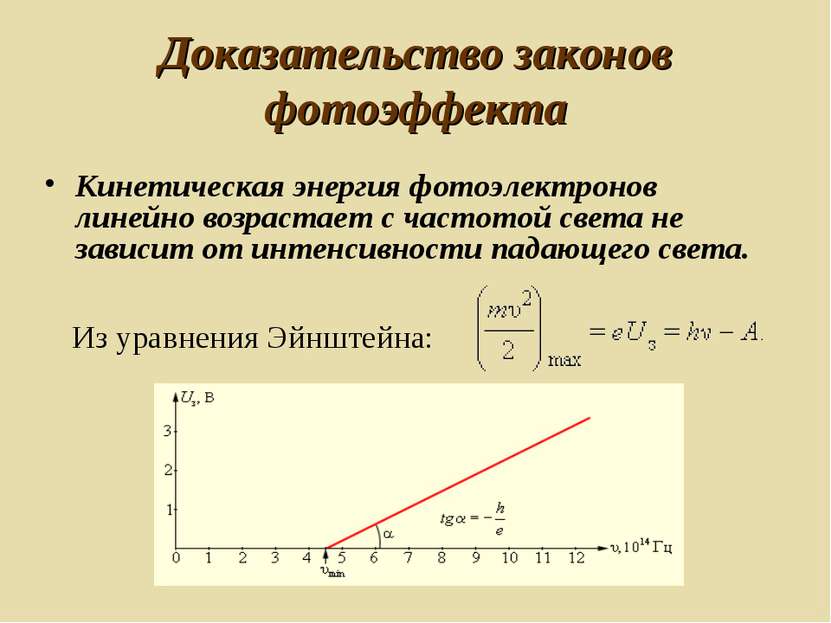
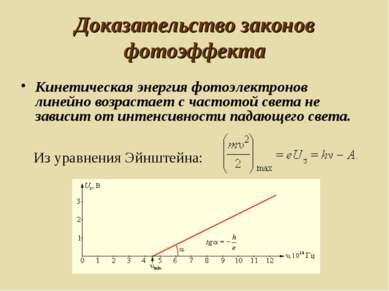Доказательство законов фотоэффекта Из уравнения Эйнштейна: Кинетическая энергия фотоэлектронов линейно возрастает с частотой света не зависит от интенсивности падающего света.
Cлайд 25
Доказательство законов фотоэффекта Минимальная частота света соответствует Wк=0, то или . Для каждого вещества существует красная граница фотоэффекта, т. е. существует наименьшая частота min, при которой еще возможен фотоэффект. Эти формулы позволяют определить работу выхода A электронов из металла.
Cлайд 26
Работа выхода Среди металлов наименьшей работой выхода обладают щелочные металлы. Например, у натрия A = 1,9 эВ, что соответствует красной границе фотоэффекта λкр ≈ 680 нм. Поэтому соединения щелочных металлов используют для создания катодов в фотоэлементах, предназначенных для регистрации видимого света.
Cлайд 27
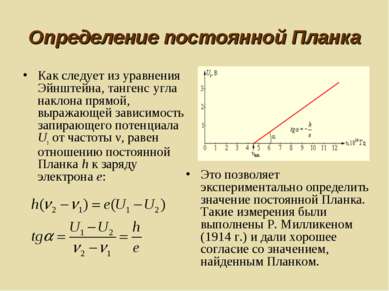Определение постоянной Планка Как следует из уравнения Эйнштейна, тангенс угла наклона прямой, выражающей зависимость запирающего потенциала Uз от частоты ν, равен отношению постоянной Планка h к заряду электрона e: Это позволяет экспериментально определить значение постоянной Планка. Такие измерения были выполнены Р. Милликеном (1914 г.) и дали хорошее согласие со значением, найденным Планком.
