X
Код презентации скопируйте его
Теория вероятностей. Треугольник Паскаля
Скачать эту презентацию
Презентация на тему Теория вероятностей. Треугольник Паскаля
Скачать эту презентациюCлайд 1
Хулиган Вася После уроков хулиган Вася решил бросать круглый камень диаметром 0,75 дм в окно защищенное сеткой с ячейками 1 дм на 1 дм. С какой вероятностью Вася разобьет окно (камень пролетит сквозь ячейку не коснувшись её краев), если он кидает не целясь и всегда попадает в сетку. Наука превыше наказания Геометрическая вероятность
Cлайд 2
Перестановки Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Число возможных перестановок из n элементов вычисляется по формуле Pn=n!=1•2•3•…•(n-2)(n-1)n
Cлайд 3
Немного истории: Первое упоминание треугольной последовательности биномиальных коэффициентов встречается в комментарии индийского математика X в. Халаюдхи. Около 1100 года треугольник исследовал Омар Хайям и в Иране это «треугольник Хайяма». В Китае считают что изобрёл его китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). Назад В 1655 году вышла книга Блеза Паскаля о треугольнике Паскаля, однако:
Cлайд 4
Законы математики, имеющие какое-либо отношение к реальному миру, ненадежны, а надежные математические законы не имеют отношения к реальному миру. Альберт Эйнштейн
Cлайд 5
Содержание
Cлайд 6
Таким образом вероятность равна 4/5040=1/1260
Cлайд 7
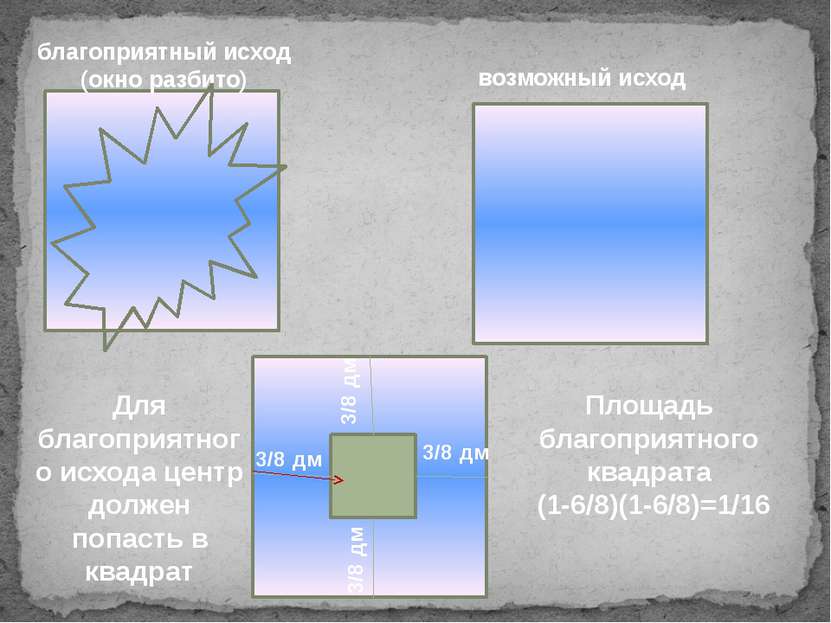
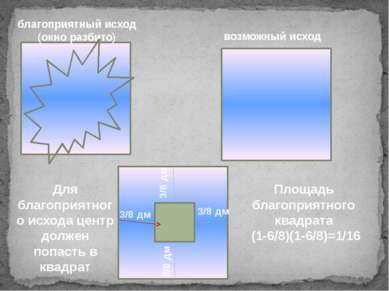
благоприятный исход (окно разбито) возможный исход Для благоприятного исхода центр должен попасть в квадрат 3/8 дм 3/8 дм 3/8 дм 3/8 дм Площадь благоприятного квадрата (1-6/8)(1-6/8)=1/16
Cлайд 8
Игральные кубики Найдите, вероятность того, что при одновременном бросании двух кубиков сумма на их гранях будет равна 5
Cлайд 9
Немного истории Найдем вероятность выпадения герба на монете: Равновозможных исходов: 2 Благоприятных исходов: 1 Итого: ½ В таблице приведены результаты экспериментов частоты выпадения герба До испытаний … и после Количество испытаний Бюффон 4040 0,507 Де Морган 4092 0,5005 Джевонс 20480 0,5068 Романовский 80640 0,4923 Пирсон 24000 0,5005 Феллер 10000 0,4979
Cлайд 10
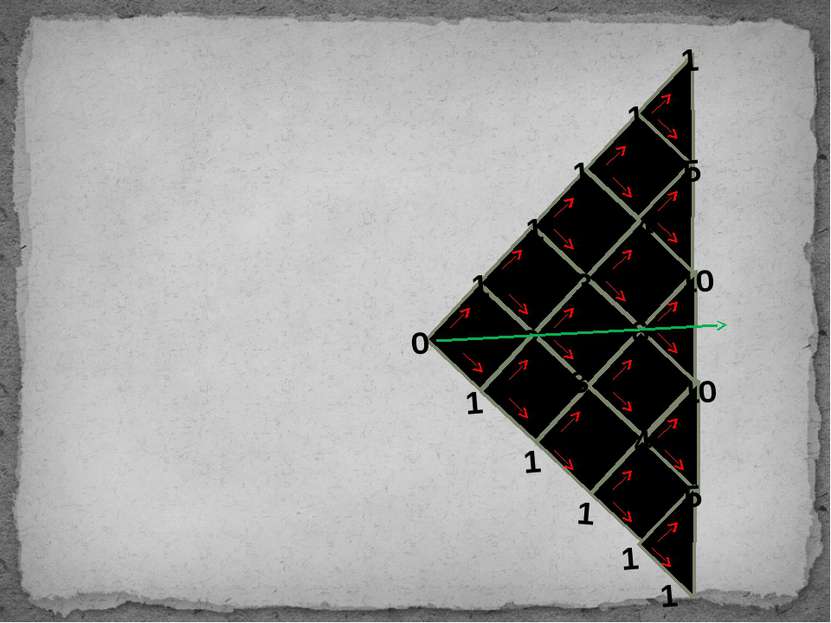
Рассмотрим задачу: за один шаг точка (частица) продвинется на 1 вниз или на 1 вверх. На горизонтальной оси будем откладывать число шагов, а на вертикальной положение точки. Блуждание по прямой Математика может открыть определенную последовательность даже в хаосе. Гертруда Стайн
Cлайд 11
Cлайд 12
Блуждание такого рода осуществляется в специальном приборе – доска Гальтона В меню
Cлайд 13
Формула бинома Ньютона и треугольник Паскаля. Действительно, 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 (a+b)1=1a+1b (a+b)2=1a2+2ab+1b2 (a+b)3=1a3+3a2b+3ab2+1b3 (a+b)4=1a4+4a3b+6a2b2+4ab3+1b4 В меню Обозначим число, стоящее на пересечении к-го столбца и n-ой строки за
Cлайд 14
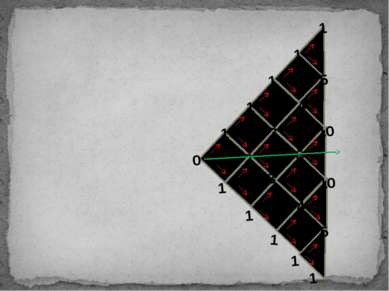
Проведем эксперимент У нас есть 16 различных траекторий блуждания точки для 4 шагов. Пронумеруем их от 0 до 15 и представим в двоичной системе счисления . Цифра 0 означает, что точка идет на 1 вниз, а цифра 1,соответственно, на 1 вверх. В столбце 3 показаны конечные положения точки через 4 шага. Будем наугад вытаскивать карточки из набора и вести учет появлениям чисел из 3 столбика. Подсчитаем относительную частоту и сравним с расчитанной. 00010101010… Пример перевода 0 0000 -4 1 0001 -2 2 0010 -2 3 0011 0 4 0100 -2 5 0101 0 6 0110 0 7 0111 2 8 1000 -2 9 1001 0 10 1010 0 11 1011 2 12 1100 0 13 1101 2 14 1110 2 15 1111 4
Cлайд 15
Гарднер о треугольнике Паскаля История о треугольнике …? Немного «волшебства»
Cлайд 16
В.А.Успенский «Треугольник Паскаля» М. «Наука». Главная редакция физико-математической литературы, 1979 А.Н.Колмогоров и др. «Введение в теорию вероятностей» М. «Наука». Главная редакция физико-математической литературы, 1982 Ф. Мостеллер «50 занимательных вероятностных задач с решениями» М. «Наука».Главная редакция физико-математической литературы, 1975 Я.И. Перельмана «Живая математика» М. Государственное издательство физико-математической литературы, 1962 С.Ф. Фомин «Системы счисления» М. «Наука». Главная редакция физико-математической литературы, 1968 Сайт http://arbuz.narod.ru Литература
Cлайд 17
Назад
Cлайд 18
Геометрическая вероятность Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наугад брошена точка. Предполагая, что вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от её расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется по формуле P=площадьg/площадьG Назад
Cлайд 19
Назад
Cлайд 20
Назад
Cлайд 21
Назад
Cлайд 22
Назад
Cлайд 23
Назад
Cлайд 24
Треугольные числа Назад Цифры (числа) не управляют миром, но они показывают, как управляется мир. И. Гете
Cлайд 25
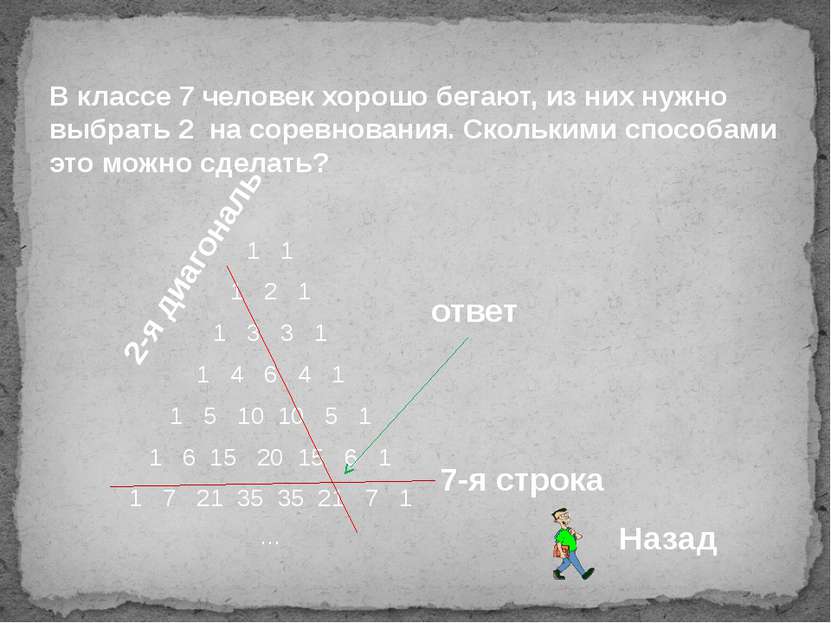
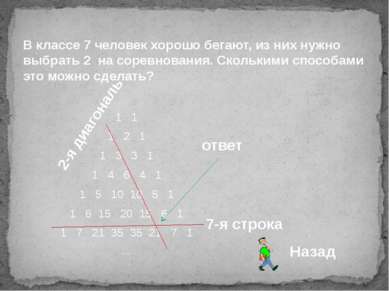
1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 … В классе 7 человек хорошо бегают, из них нужно выбрать 2 на соревнования. Сколькими способами это можно сделать? 7-я строка 2-я диагональ ответ Назад
Cлайд 26
Все внутренние члены m-й строки Паскаля делятся на m тогда и только тогда, когда m-простое. Назад
Cлайд 27
Узоры треугольника Паскаля Назад
Cлайд 28
Назад
Cлайд 29
10 молодых людей пришли в ресторан, но никак не могли усесться вокруг стола, тогда официант предложил им сесть как попало, но в следующий приход в ресторан сесть в другом порядке и после того, как будут перепробованы все варианты – обеды станут бесплатными. Когда же обед станет бесплатным? А ждать придется 10!=3628800 дней… (примерно 10000 лет)
Cлайд 30
Назад
Cлайд 31
Cлайд 32
Cлайд 33
Cлайд 34
Cлайд 35
Cлайд 36
Cлайд 37
Cлайд 38
Cлайд 39
