X
Код презентации скопируйте его
Движение по окружности
Скачать эту презентацию
Презентация на тему Движение по окружности
Скачать эту презентациюCлайд 1
Движение по окружности
Cлайд 2
Изучить основные характеристики движения: угловая скорость; линейная скорость; ускорение; период. Рассмотреть всевозможные случаи применения движения по окружности: вращение тела; движение на поворотах; движение планет; движение заряженных частиц. Цели
Cлайд 3
Линейная скорость, v (м/с). Угловая скорость, (рад/с). Центростремительное ускорение, а (м/с²). Период обращения, Т (с). Частота обращения, (рад/с). Характеристики движения
Cлайд 4
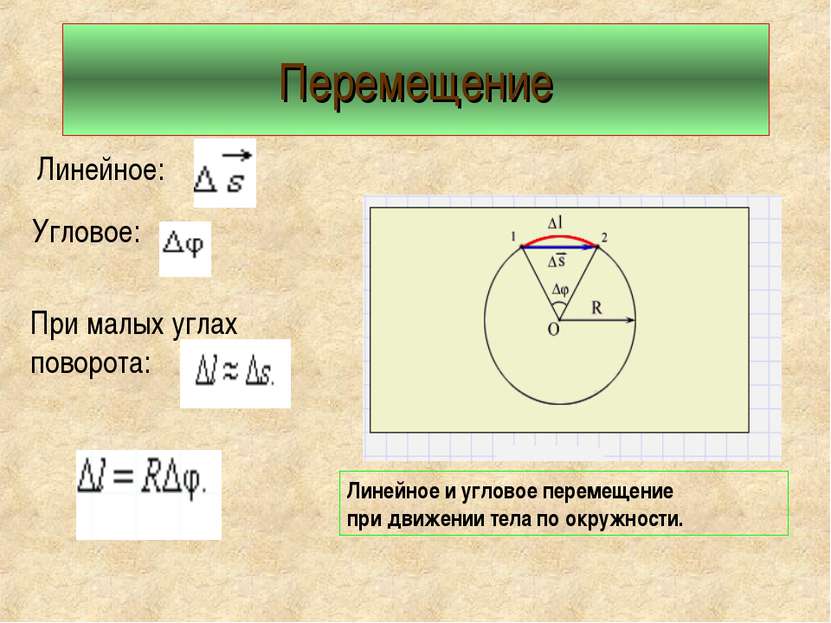
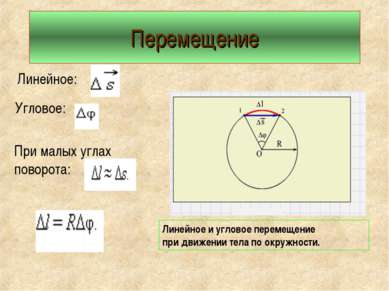Перемещение Линейное: Угловое: При малых углах поворота: Линейное и угловое перемещение при движении тела по окружности.
Cлайд 5
Траектория движения
Cлайд 6
Траектория движения
Cлайд 7
Траектория движения
Cлайд 8
Траектория движения
Cлайд 9
Скорость V=s/t = /t Модель. Скорость тела при движении по окружности. V= R
Cлайд 10
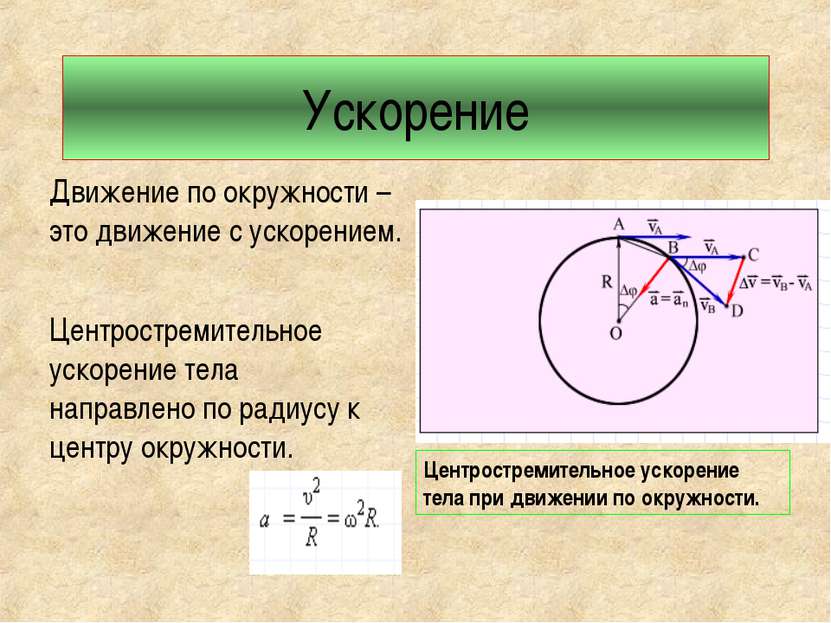
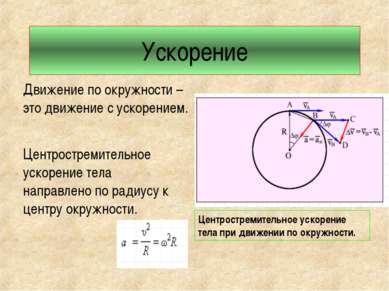Ускорение Движение по окружности – это движение с ускорением. Центростремительное ускорение тела направлено по радиусу к центру окружности. Центростремительное ускорение тела при движении по окружности.
Cлайд 11
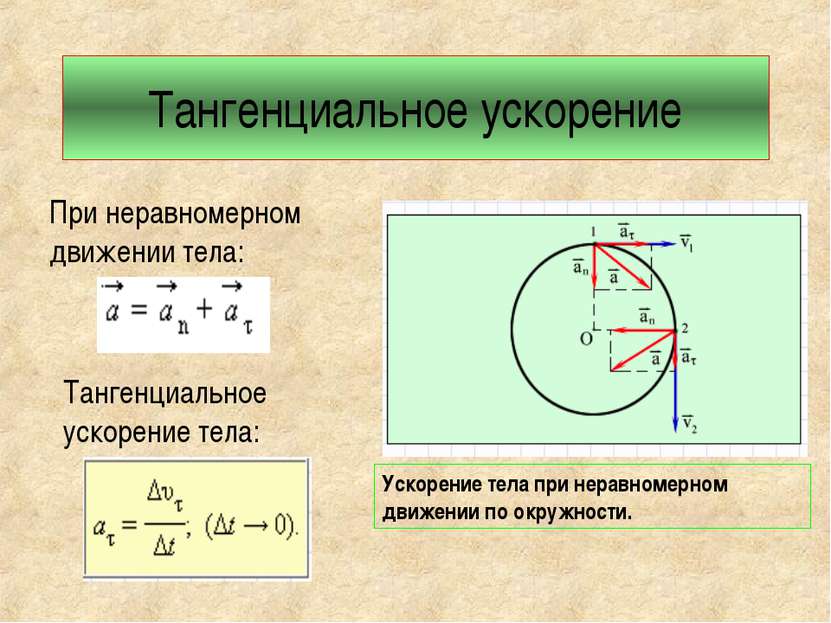
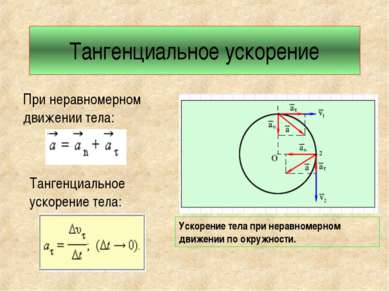Тангенциальное ускорение Ускорение тела при неравномерном движении по окружности. При неравномерном движении тела: Тангенциальное ускорение тела:
Cлайд 12
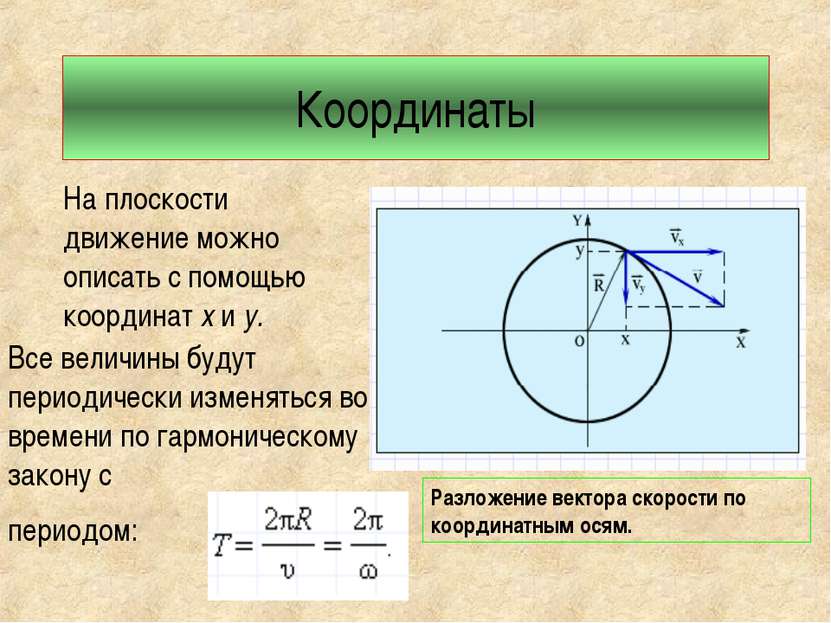
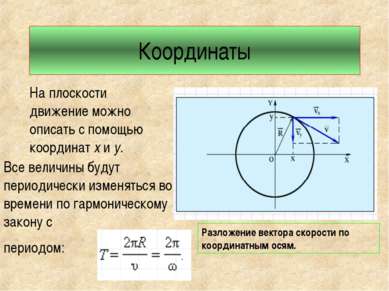Координаты На плоскости движение можно описать с помощью координат х и у. Все величины будут периодически изменяться во времени по гармоническому закону с периодом: Разложение вектора скорости по координатным осям.
Cлайд 13
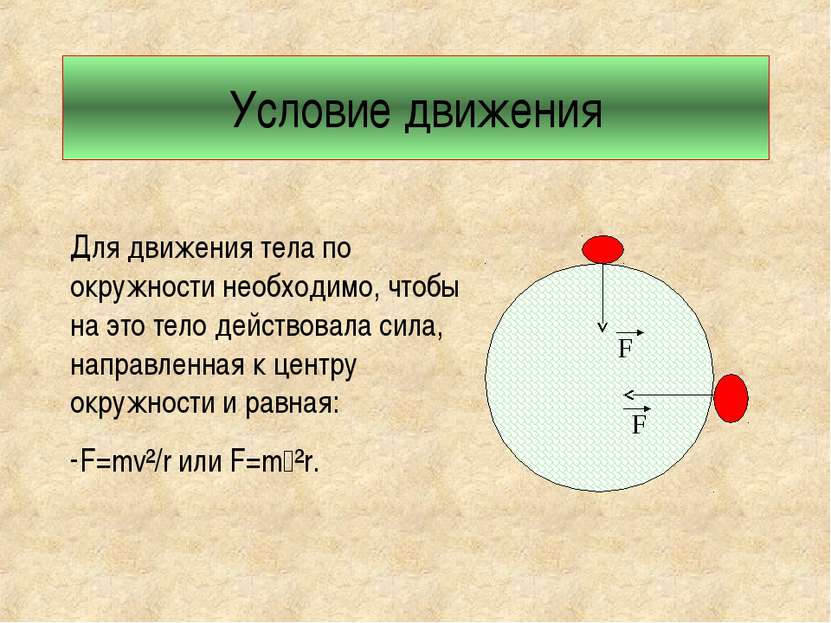
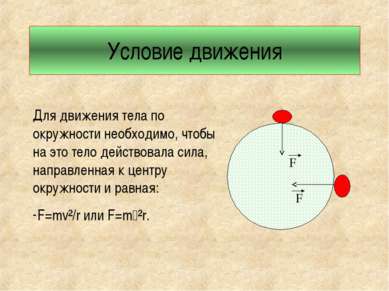Условие движения Для движения тела по окружности необходимо, чтобы на это тело действовала сила, направленная к центру окружности и равная: F=mv²/r или F=m ²r. F F
Cлайд 14
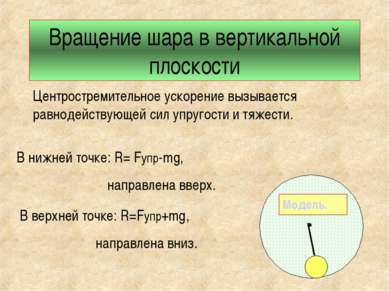Вращение шара в вертикальной плоскости Центростремительное ускорение вызывается равнодействующей сил упругости и тяжести. В нижней точке: R= Fупр-mg, направлена вверх. В верхней точке: R=Fупр+mg, направлена вниз. Модель.
Cлайд 15
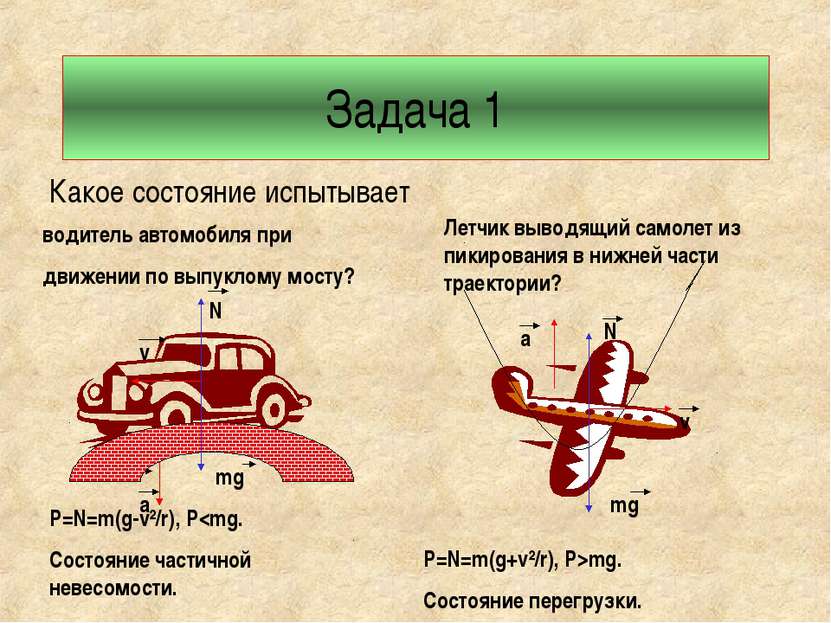
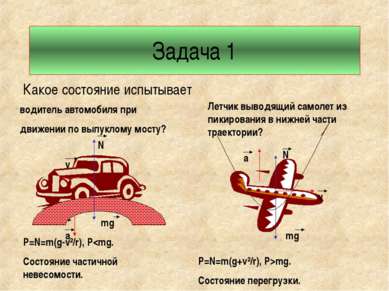Задача 1 Какое состояние испытывает водитель автомобиля при движении по выпуклому мосту? Летчик выводящий самолет из пикирования в нижней части траектории? N mg v a P=N=m(g-v²/r), Pmg. Состояние перегрузки.
Cлайд 16
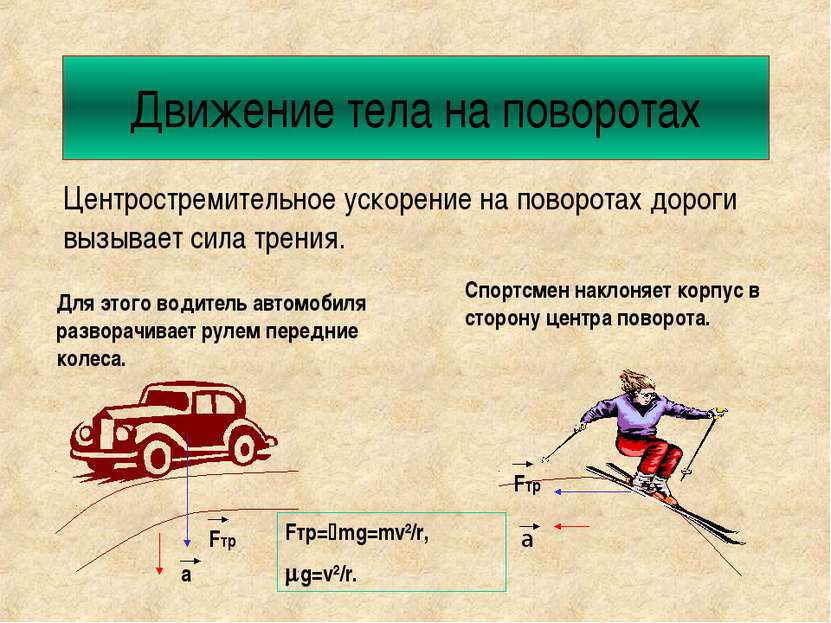
Движение тела на поворотах Центростремительное ускорение на поворотах дороги вызывает сила трения. Для этого водитель автомобиля разворачивает рулем передние колеса. Спортсмен наклоняет корпус в сторону центра поворота. Fтр а Fтр а Fтр= mg=mv²/r, g=v²/r.
Cлайд 17
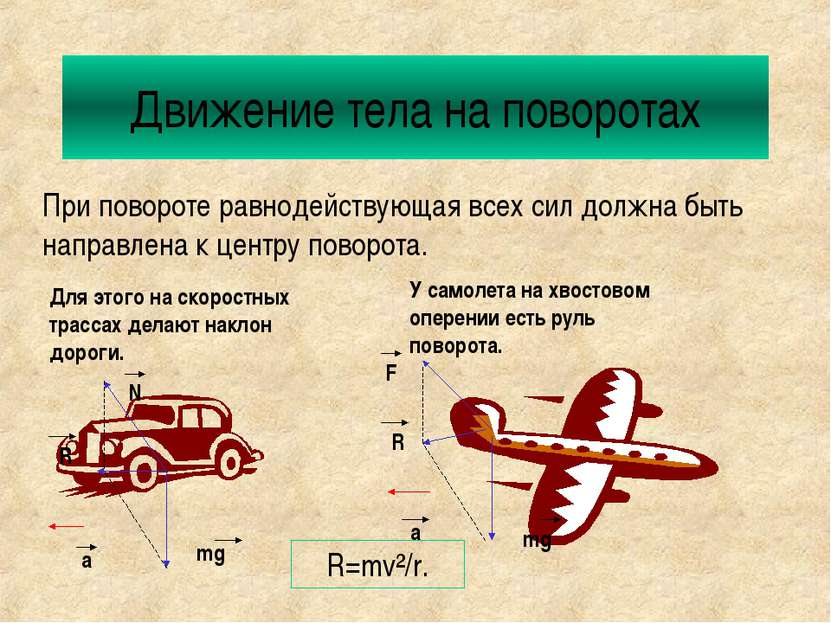
Движение тела на поворотах При повороте равнодействующая всех сил должна быть направлена к центру поворота. Для этого на скоростных трассах делают наклон дороги. У самолета на хвостовом оперении есть руль поворота. mg a N R F mg R a R=mv²/r.
Cлайд 18
Движение тел в гравитационном поле Сила гравитационного притяжения сообщает и небесным телам центростремительное ускорение. Траектории: 1-круговая; 2,3 –эллиптические; 4-параболическая; 5-гиперболическая; 6- траектория Луны. Модель.
Cлайд 19
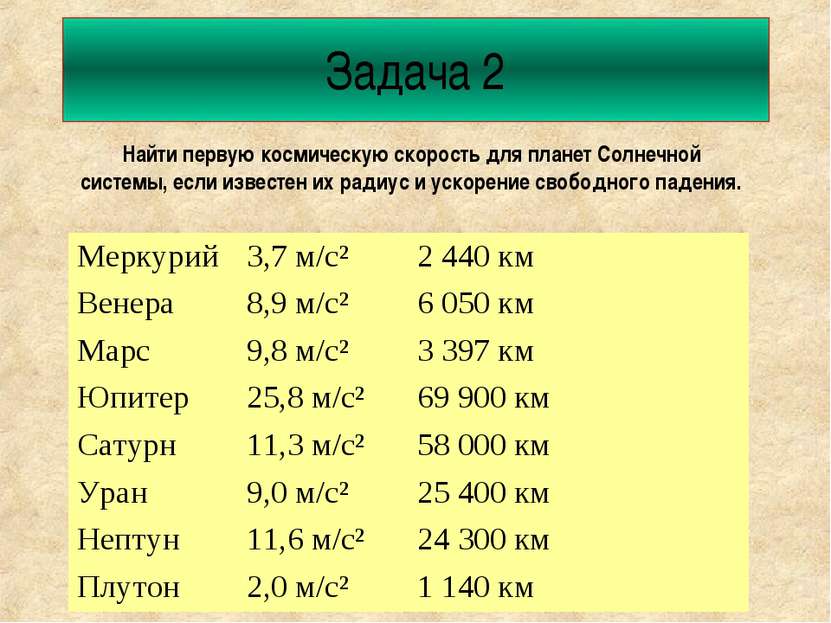
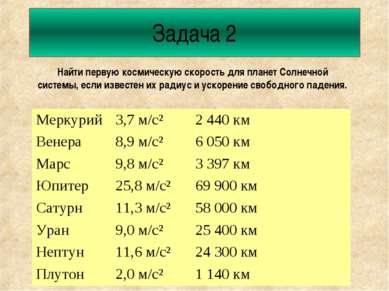Задача 2 Найти первую космическую скорость для планет Солнечной системы, если известен их радиус и ускорение свободного падения.
Cлайд 20
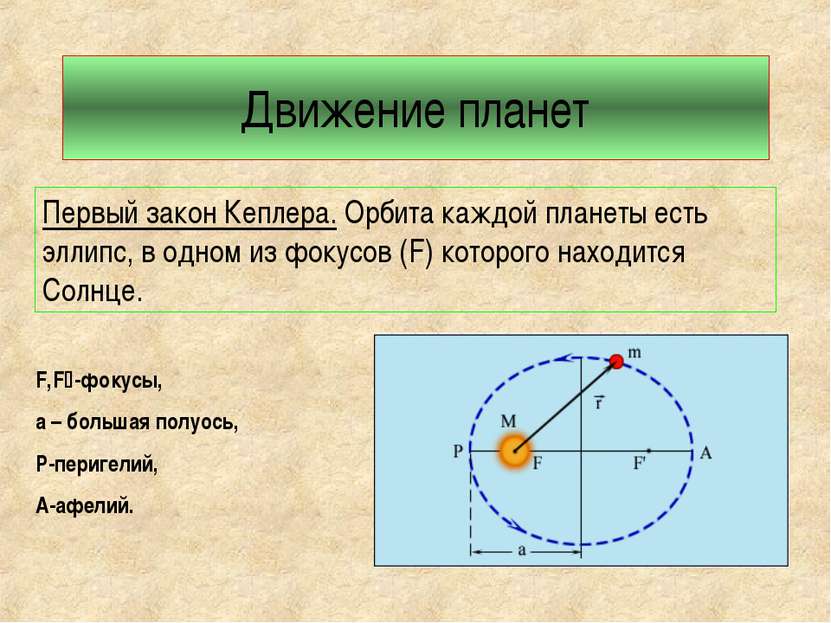
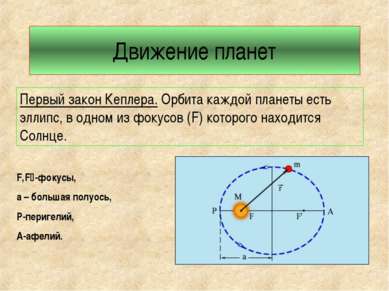Движение планет Первый закон Кеплера. Орбита каждой планеты есть эллипс, в одном из фокусов (F) которого находится Солнце. F,F -фокусы, а – большая полуось, Р-перигелий, А-афелий.
Cлайд 21
Движение планет Второй закон Кеплера. Радиус-вектор планеты в равные промежутки времени описывает равные площади. Третий закон Кеплера.
Cлайд 22
Cлайд 23
Cлайд 24
Задача 3 Найти период обращения планет земной группы,если известно их среднее расстояние от Солнца. Тз= 1 год, аз= 1 а.е.
Cлайд 25
Задача 4 На каком расстоянии от Солнца находятся планеты-гиганты, если известен их период обращения? Тз= 1 год, аз= 1 а.е.
Cлайд 26
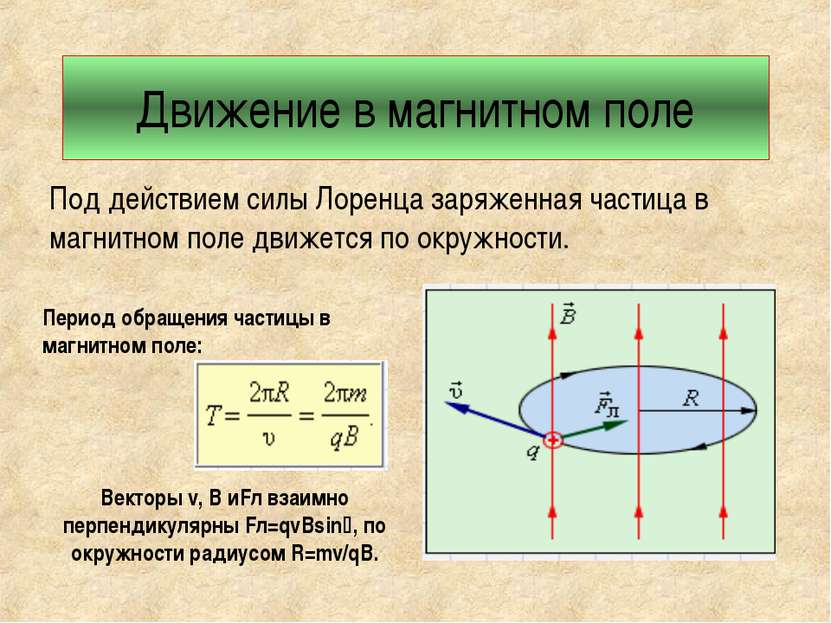
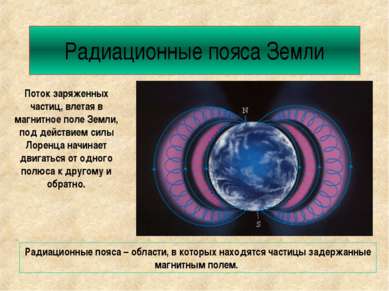
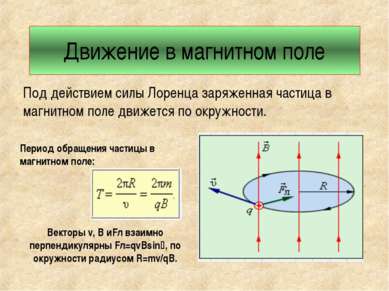Движение в магнитном поле Под действием силы Лоренца заряженная частица в магнитном поле движется по окружности. Период обращения частицы в магнитном поле: Векторы v, В иFл взаимно перпендикулярны Fл=qvBsin , по окружности радиусом R=mv/qB.
Cлайд 27
Радиационные пояса Земли Поток заряженных частиц, влетая в магнитное поле Земли, под действием силы Лоренца начинает двигаться от одного полюса к другому и обратно. Радиационные пояса – области, в которых находятся частицы задержанные магнитным полем.
Cлайд 28
Строение атома Планетарная модель атома Резерфорда: электроны движутся вокруг ядра атома по эллипсам.
