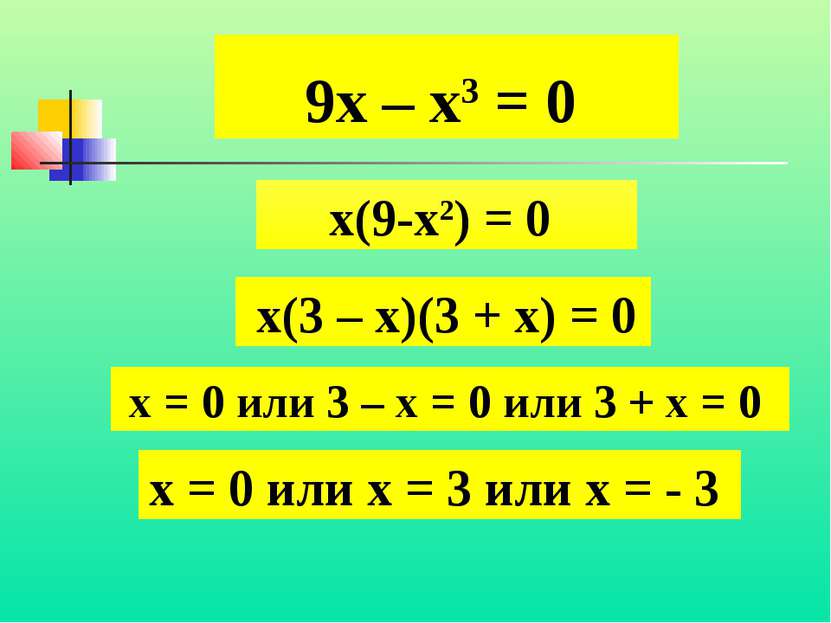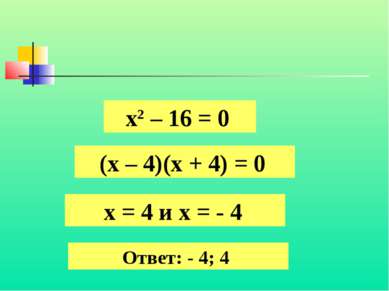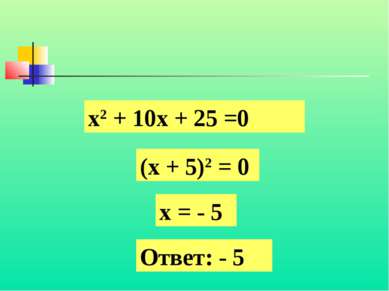X
Код презентации скопируйте его
Разложение на множители
Скачать эту презентацию
Презентация на тему Разложение на множители
Скачать эту презентациюCлайд 1
Разложение на множители.
Cлайд 2
Что называют разложением многочлена на множители? a2 – 5ab = a2 – 25 = a2 – 36 = Разложите на множители а(а – 5b) (a – 5) (а + 5) (a – 6) (а + 6)
Cлайд 3
Разложите на множители 8 – a3 = x3 + 64 = a3 – 25а = а(а + 4b) a2 + 4ab = (2 – a)(4 + 2а + a2 (х + 4)(х2 – 4х + 16) а(а – 5)(а + 5)
Cлайд 4
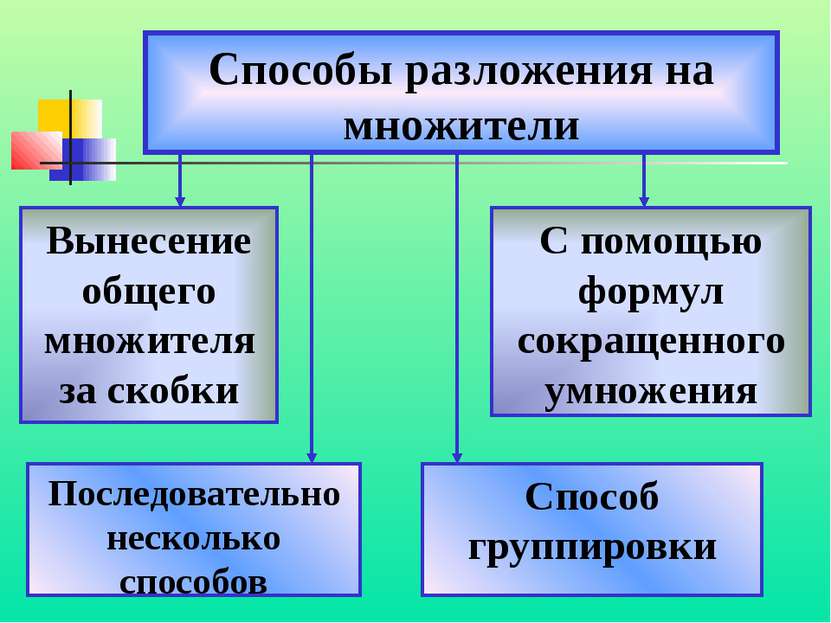
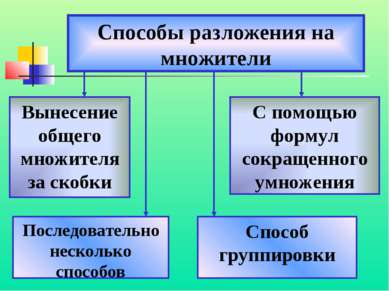Способы разложения на множители Вынесение общего множителя за скобки Способ группировки С помощью формул сокращенного умножения Последовательно несколько способов
Cлайд 5
Решите уравнения (х – 2)(х + 2) = 0 Х= 2 и х = - 2 Ответ: - 2; 2
Cлайд 6
х2 – 16 = 0 (х – 4)(х + 4) = 0 х = 4 и х = - 4 Ответ: - 4; 4
Cлайд 7
х2 + 10х + 25 =0 (х + 5)2 = 0 х = - 5 Ответ: - 5
Cлайд 8
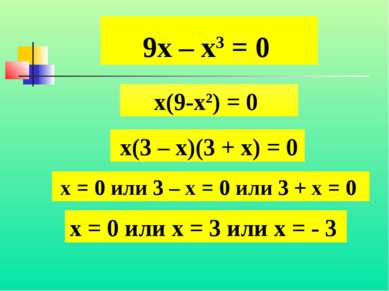9х – х3 = 0 х(9-х2) = 0 х(3 – х)(3 + х) = 0 х = 0 или 3 – х = 0 или 3 + х = 0 х = 0 или х = 3 или х = - 3
Cлайд 9
Найдите значение числового выражения Разложение на множители позволило нам сократить дробь. 532-472 612-392 Самое эффективное решение – дважды воспользоваться формулой разности квадратов: 532-472 612-392 (53-47)(53+47) (61-39)(61+39) = 6•100 22•100 = = 6 22 = 3 11
Cлайд 10
Алгоритм отыскания общего множителя нескольких одночленов 1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем Вынесение общего множителя за скобки
Cлайд 11
Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени. 3. Произведение коэффициента, найденного на первом шаге, является общим множителем, который выносят за скобки.
Cлайд 12
Разложить на множители: -x4y3-2x3y2+5x2. Воспользуемся сформулированным алгоритмом. Наибольший общий делитель коэффициентов –1, -2 и 5 равен 1. Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2.
Cлайд 13
Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки. Вывод: за скобки можно вынести x2, в данном случае целесообразнее вынести -x2. -x4y3-2x3y2+5x2 = -x2(x2y3+2xy2-5) Получим:
Cлайд 14
Способ группировки Рассмотрим пример: разложите на множители многочлен х3+х2у– 4у – 4х = (х2+х2у) – (4х+4у) = = х2 (х + у) – 4(х + у) = х + у)(х2 – 4) = (х + у)(х2 – 4) = (х + у)(х – 2)(х + 2)
Cлайд 15
bx2 + 2b2 – b3 – 2x2 = (bx2 – b3) – (2x2–2b2)= = b(x2 – b2) –2(x2 – b2) = (b – 2)(x2 – b2) = (b – 2)(x – b)(x + b) Способ группировки
Cлайд 16
Разложение многочлена на множители с помощью формул сокращенного умножения Вспомните эти формулы: a2-b2=(a-b)(a+b); a3-b3=(a-b)(a2+ab+b2); a3+b3=(a+b)(a2-ab+b2); a2+2ab+b2=(a+b)2; a2-2ab+b2=(a-b)2.
Cлайд 17
Первую из этих формул можно применять к выражению, представляющему собой разность квадратов (безразлично чего – чисел, одночленов, многочленов), вторую и третью – к выражению, представляющему собой разность (или сумму) кубов; Последние две формулы применяются к трехчлену, представляющему собой полный квадрат, т.е. содержащему сумму квадратов двух выражений и удвоенное произведение тех же выражений. a2-b2=(a-b)(a+b); a3-b3=(a-b)(a2+ab+b2); a3+b3=(a+b)(a2-ab+b2); a2+2ab+b2=(a+b)2; a2-2ab+b2=(a-b)2.
Cлайд 18
Воспользовались формулой суммы кубов. а6 + 27b3 = (a2)3 + (3b)3 = = (a2 + 3b)(a4 – 3a2b + 9b2)
Cлайд 19
Х 2 4 0,8ху + 0,16у 2 Х 2 2 = 2 · 1 2 х · 0,4у + (0,4у)2 = Х 2 0,4у 2 = Воспользовались формулой квадрата разности.
Cлайд 20
Воспользовались формулой разности квадратов. х6 – 4а4 = = (х3)2 – (2а2)2 = (х3 – 2а2) (х3 + 2а2)
Cлайд 21
Разложение многочлена на множители с помощью комбинации различных приемов В математике не так часто бывает, чтобы при решении примера применялся только один прием, чаще встречаются комбинированные примеры, где сначала используется один прием, затем другой и т.д. Чтобы успешно решать такие примеры, мало знать сами приемы, надо еще уметь выработать план их последовательного применения. Иными словами, здесь нужны не только знания, но и опыт. Вот такие комбинированные примеры мы и рассмотрим.
Cлайд 22
1. Разложить на множители многочлен 36a6b3-96a4b4+64a2b5 Сначала займемся вынесением общего множителя за скобки. Рассмотрим коэффициенты 36, 96, 64. Все они делятся на 4, причем это – наибольший общий делитель, вынесем его за скобки. Во все члены многочлена входит переменная a (соответственно a6, a4, a2), поэтому за скобки можно вынести a2. Точно так же во все члены многочлена входит переменная b (соответственно b3, b4, b5) – за скобки можно вынести b3.
Cлайд 23
Итак, за скобки вынесем 4a2b3. Тогда получим: 36a6b3-96a4b4+64a2b5 = 4a2b3(9a4-24a2b+16b2) 2) Рассмотрим трехчлен в скобках: 9a4-24a2b+16b2. Выясним, не является ли он полным квадратом. Имеем: 9a4-24a2b+16b2=(3a2)2+(4b)2-2·3a2·4b.
Cлайд 24
Все условия полного квадрата соблюдены, следовательно, 9a4-24a2b+16b2= 3) Комбинируя два приема (вынесение общего множителя за скобки и использование формул сокращенного умножения), получаем окончательный результат: (3a2-4b)2. 36a6b3-96a4b4+64a2b5=4a2b3(3a2-4b)2.
Cлайд 25
2. Разложить на множители x4+x2a2+a4 Применим метод выделения полного квадрата. Для этого представим x2a2 в виде 2x2a2-x2a2. Получим: (x2+a2)2-(xa)2= x4+x2a2+a4 = x4+2x2a2-x2a2+a4= = (x4+2x2a2+a4)-x2a2 = = (x2+a2+xa) · (х2 + а2 – ха)
Cлайд 26
3. Разложить на множители n3+3n2+2n Сначала воспользуемся тем, что n можно вынести за скобки: n(n2+3n+2). Теперь к трехчлену n2+3n+2 применим способ группировки, предварительно представив 3n в виде 2n+n. Получим:
Cлайд 27
Окончательно получаем: n2+3n+2= n2+2n+n+2 = = (n2+2n)+(n+2) = n(n+2)+(n+2) = = (n+2)(n+1). n(n+1)(n+2). n2+3n+2=
Cлайд 28
Cлайд 29
Ответы
Cлайд 30
До новых встреч!
Cлайд 31
Спасибо!
