X
Код презентации скопируйте его
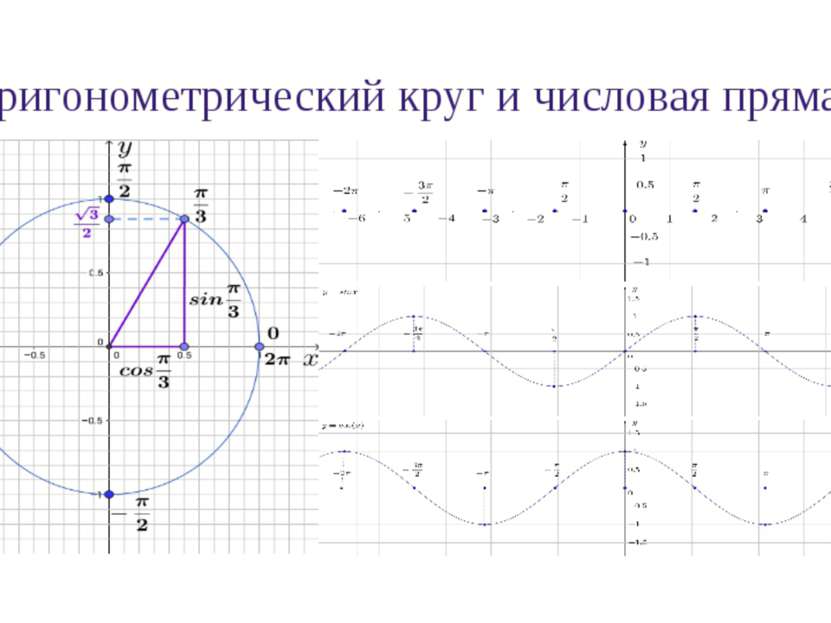
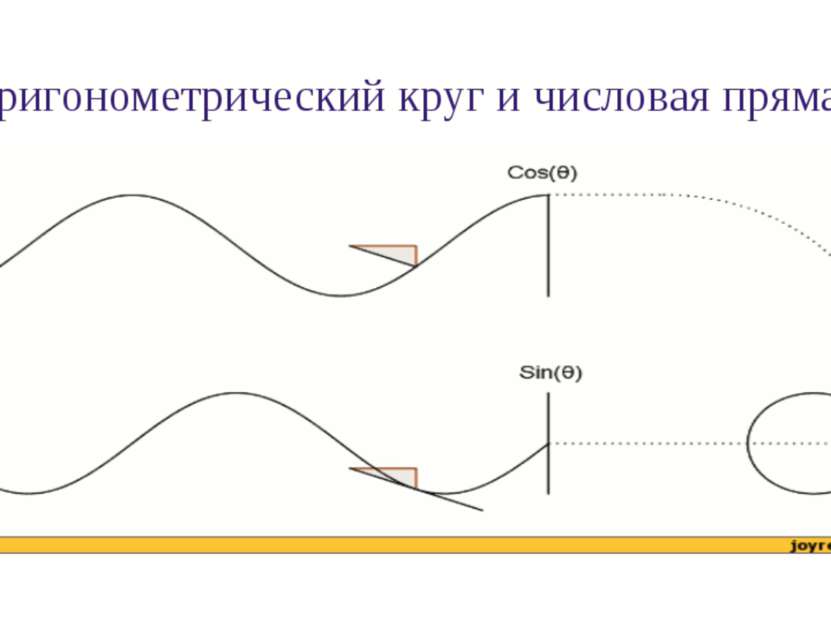
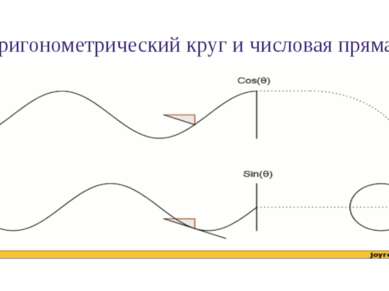
Графики функций синуса и косинуса и их свойства
Скачать эту презентацию
Презентация на тему Графики функций синуса и косинуса и их свойства
Скачать эту презентациюCлайд 1
Графики и свойства тригонометрических функций синуса и косинуса
Cлайд 2
График функции y = sinx
Cлайд 3
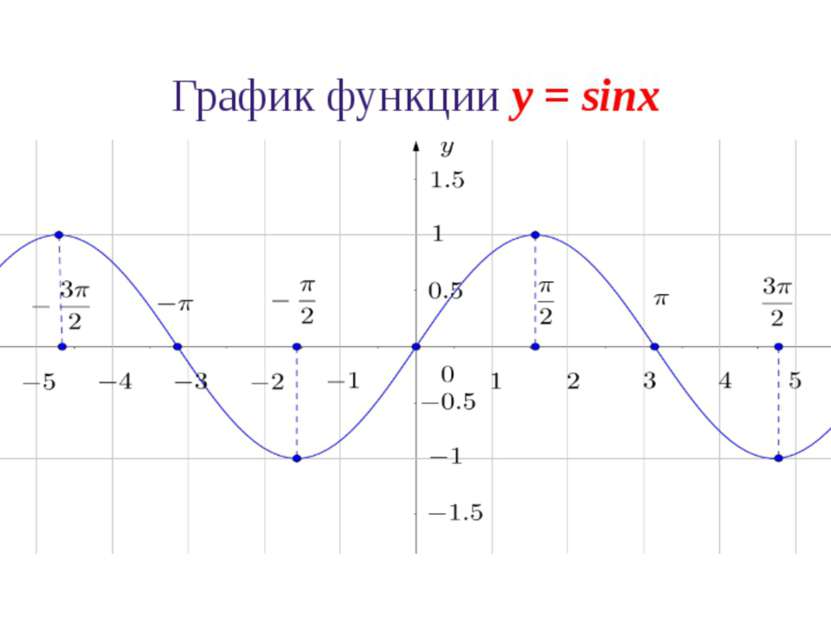
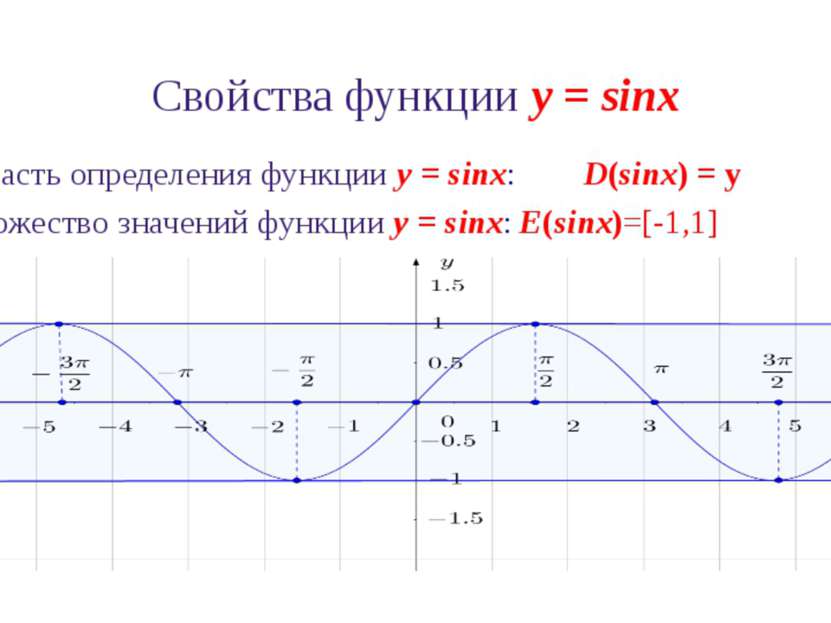
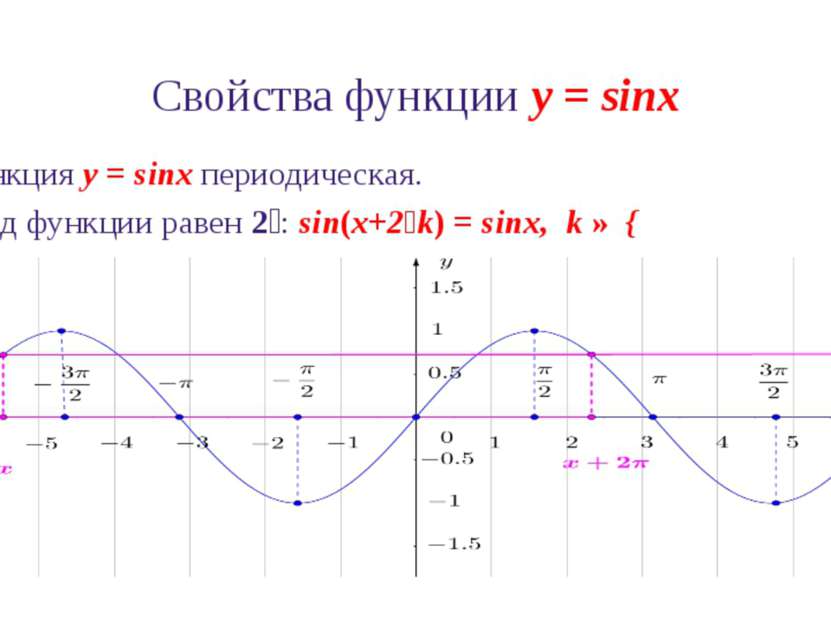
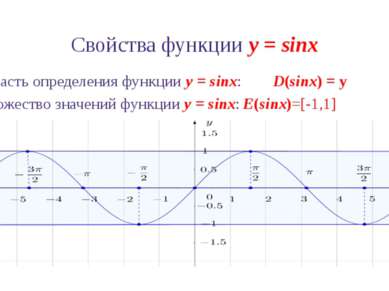
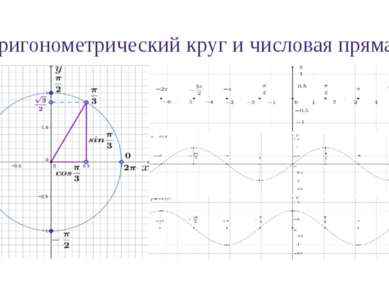Свойства функции y = sinx 1. Область определения функции y = sinx: D(sinx) = ℝ 2. Множество значений функции y = sinx: E(sinx)=[-1,1]
Cлайд 4
Тригонометрический круг и числовая прямая
Cлайд 5
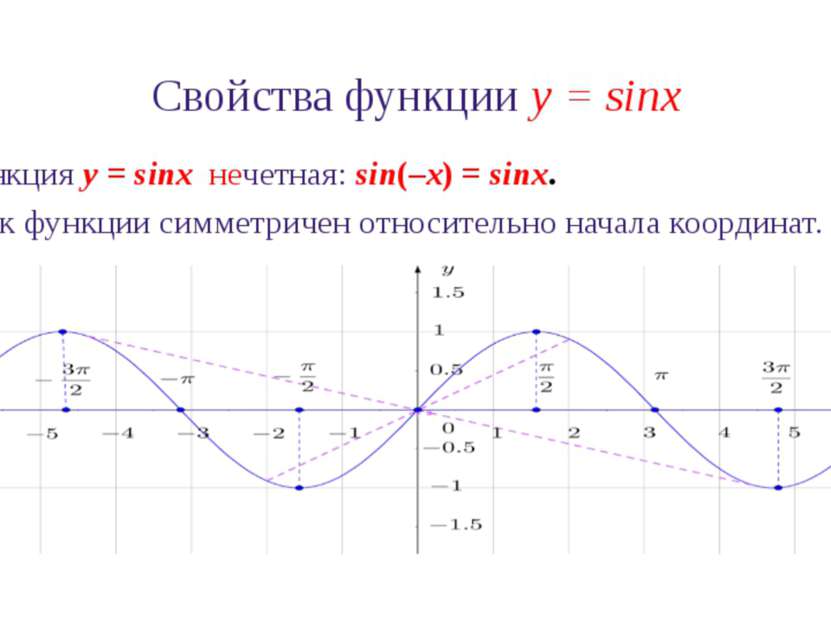
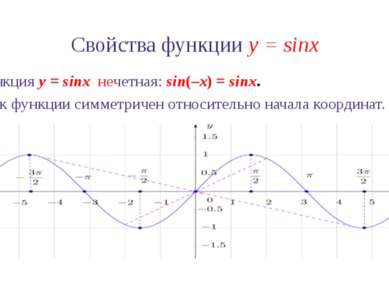
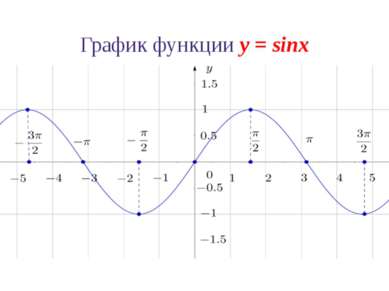Свойства функции y = sinx 3. Функция y = sinx нечетная: sin(–x) = sinx. График функции симметричен относительно начала координат.
Cлайд 6
Свойства функции y = sinx 4. Функция y = sinx периодическая. Период функции равен 2
Cлайд 7
Свойства функции y = sinx 5. Нули функции y = sinx: sinx = 0 при x =
Cлайд 8
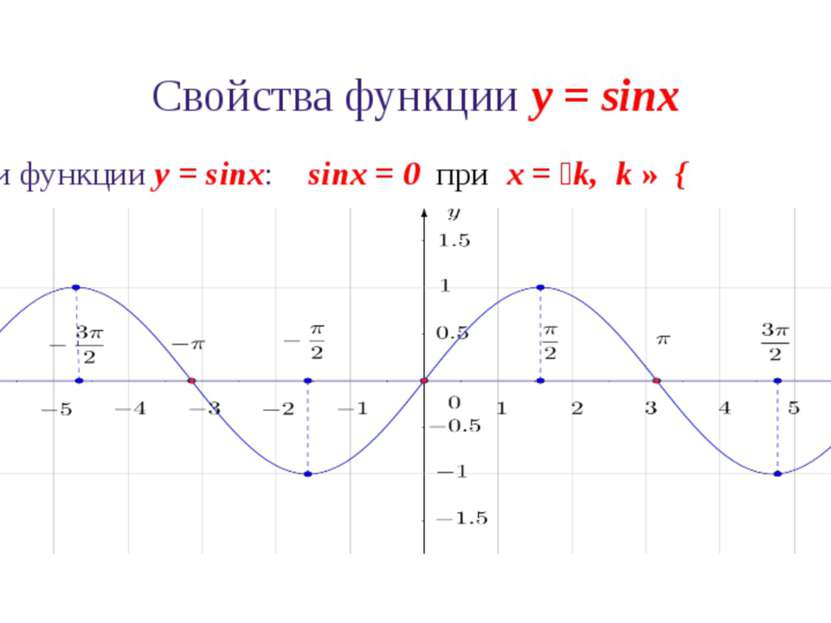
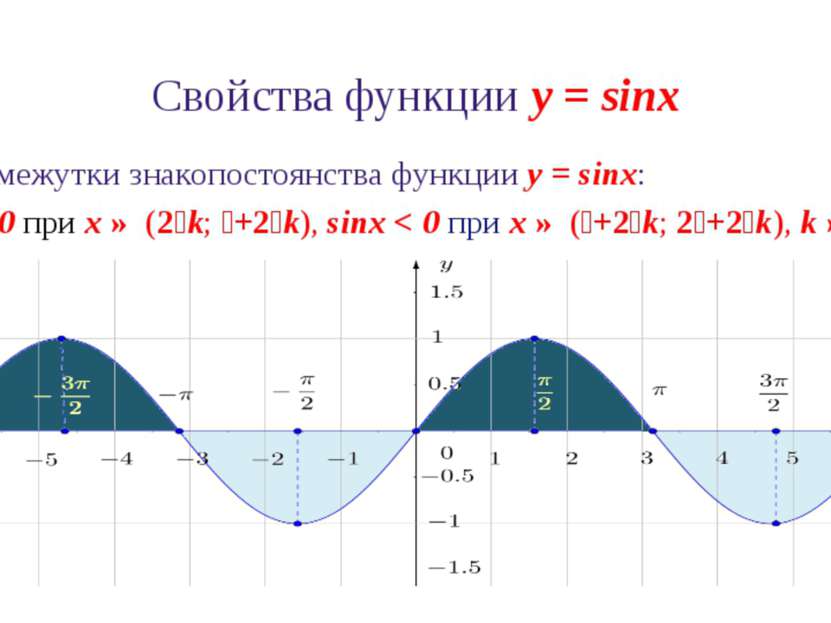
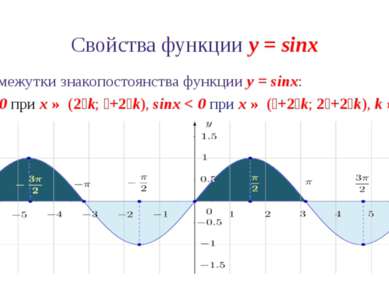
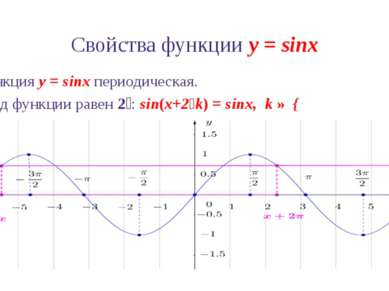Свойства функции y = sinx 6. Промежутки знакопостоянства функции y = sinx: sinx > 0 при x ∈ (2
Cлайд 9
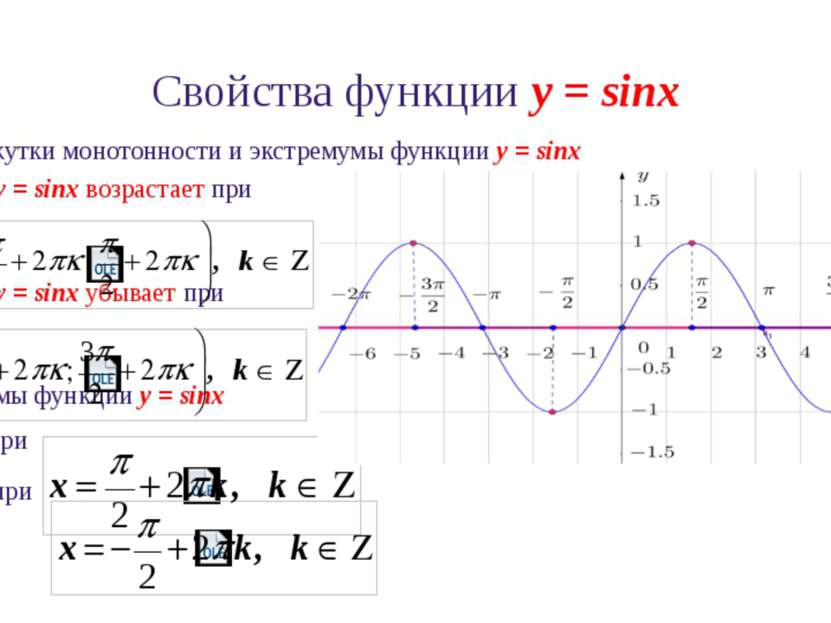
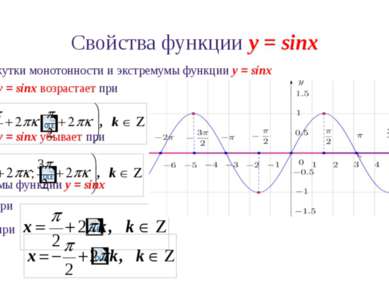
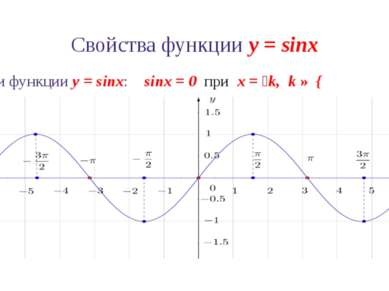Свойства функции y = sinx 7. Промежутки монотонности и экстремумы функции y = sinx Функция y = sinx возрастает при Функция y = sinx убывает при Экстремумы функции y = sinx ymax= 1 при ymin= -1 при
Cлайд 10
График функции y = cosx
Cлайд 11
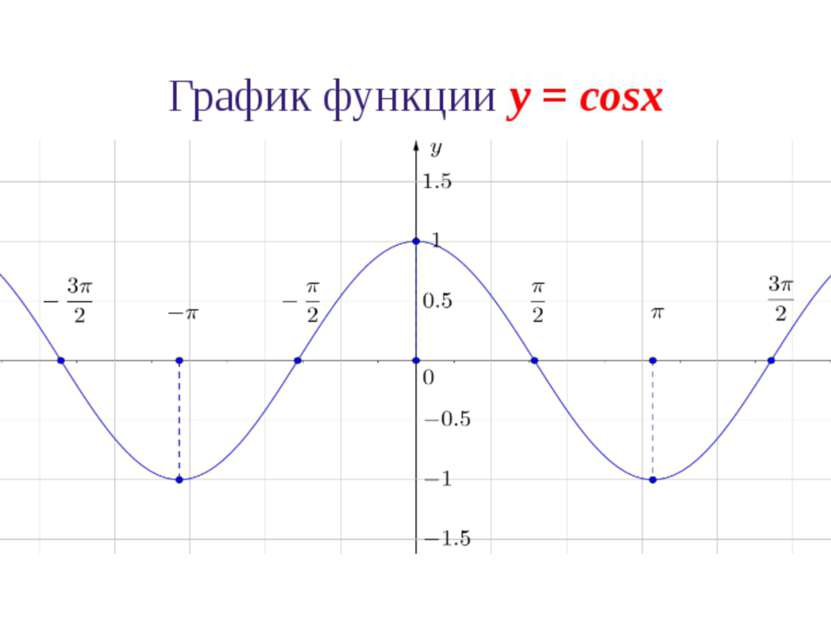
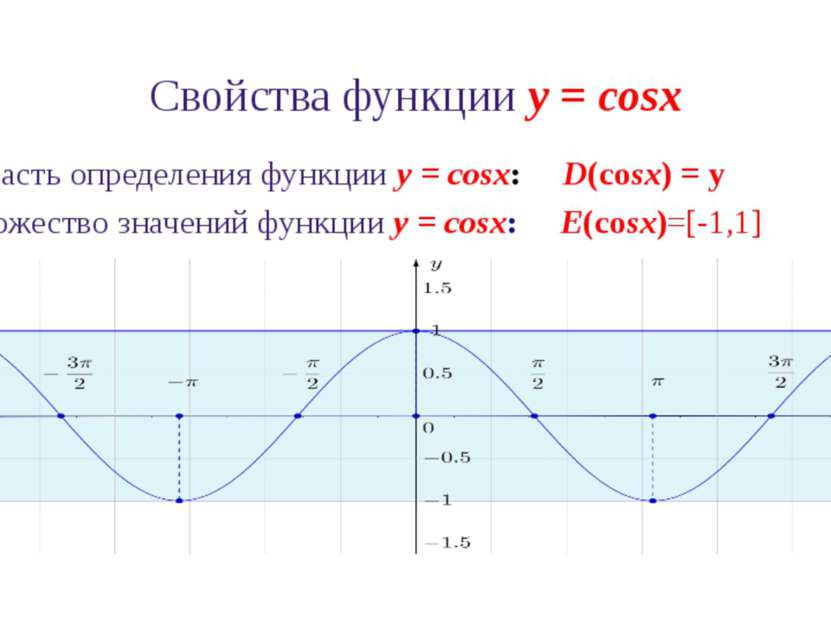
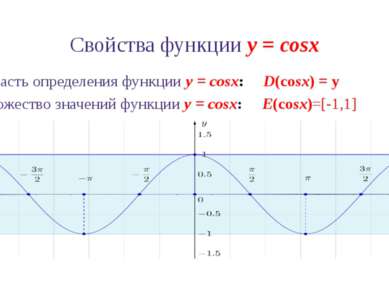
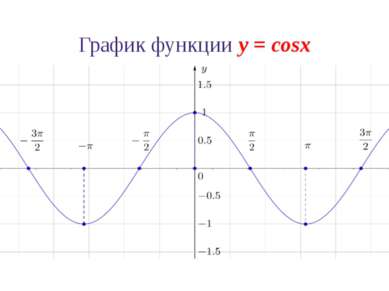
Свойства функции y = cosx 1. Область определения функции y = cosx: D(cosx) = ℝ 2. Множество значений функции y = cosx: E(cosx)=[-1,1]
Cлайд 12
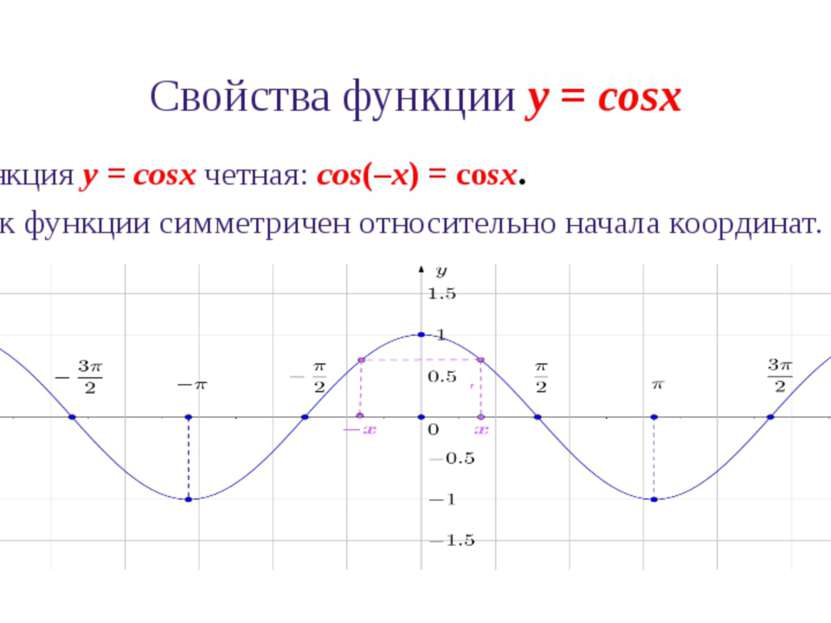
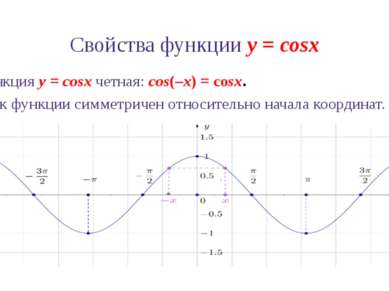
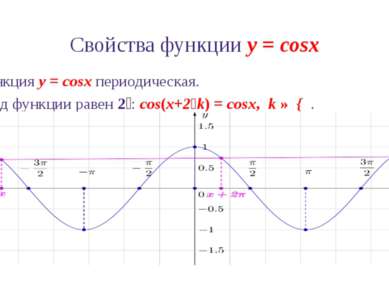
Свойства функции y = cosx 3. Функция y = cosx четная: cos(–x) = cosx. График функции симметричен относительно начала координат.
Cлайд 13
Свойства функции y = cosx 4. Функция y = cosx периодическая. Период функции равен 2
Cлайд 14
Свойства функции y = cosx 5. Нули функции y = cosx: cosx = 0 при x =
Cлайд 15
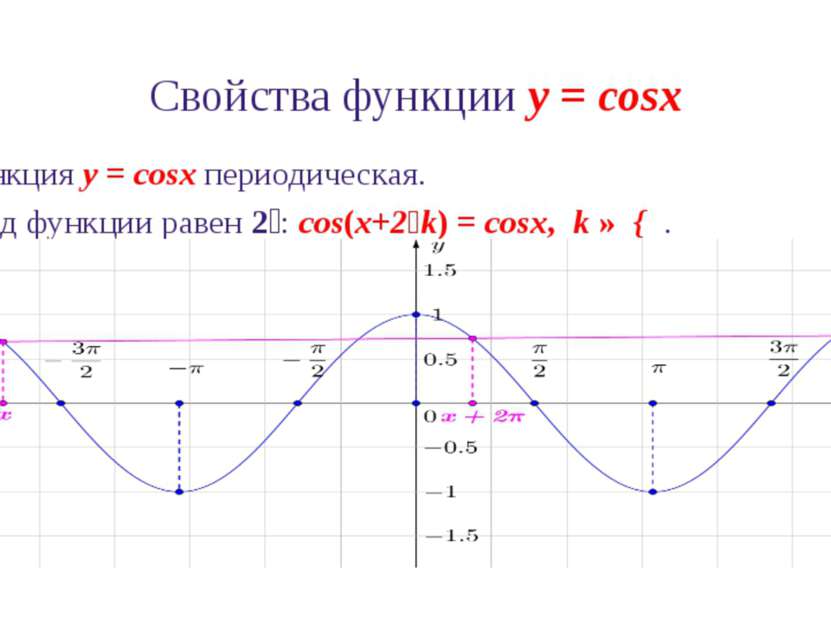
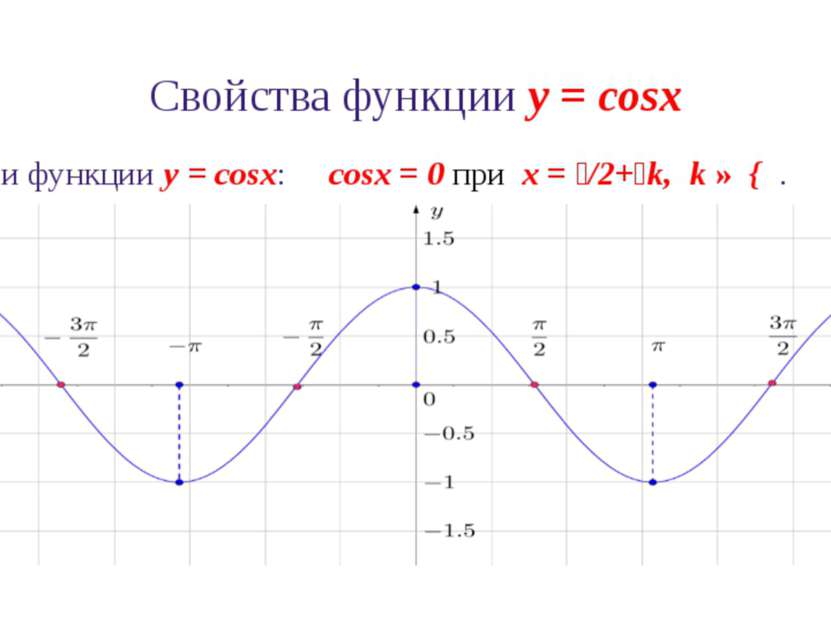
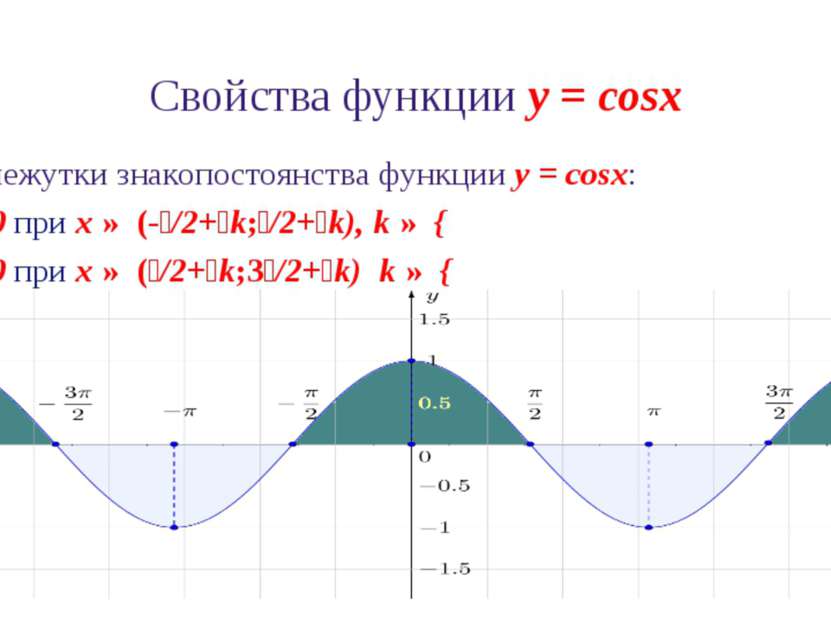
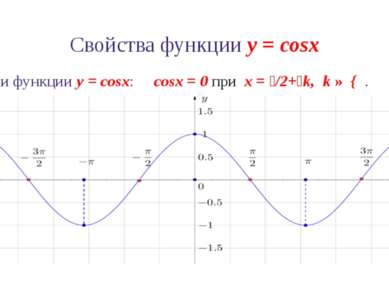
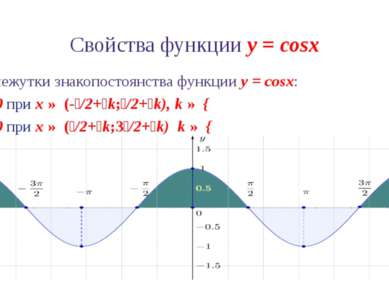
Свойства функции y = cosx 6. Промежутки знакопостоянства функции y = cosx: cosx > 0 при x ∈ (-
Cлайд 16
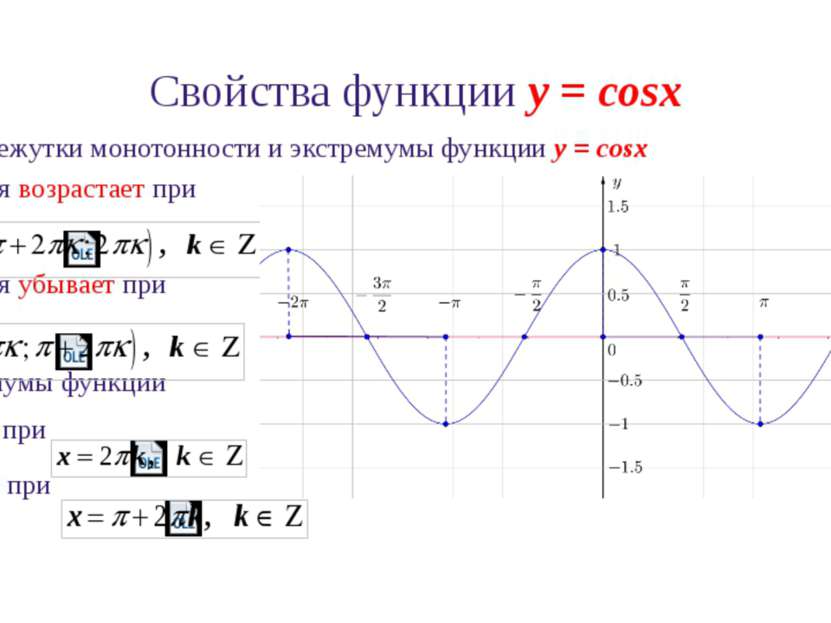
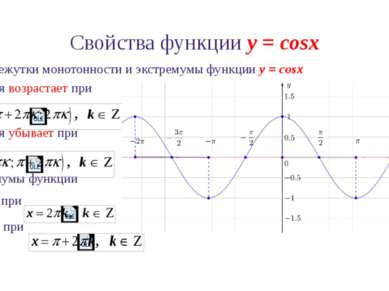
Свойства функции y = cosx 7. Промежутки монотонности и экстремумы функции y = cosx Функция возрастает при Функция убывает при Экстремумы функции ymax=1 при ymin=-1 при
Cлайд 17
Сравнение свойств функций y = sinx и y = cosx Функция y = sinx y = cosx Область определения D(sinx) =ℝ D(cosx) =ℝ Множество значений E(sinx) = [-1,1] E(cosx) = [-1,1] Четность и нечетность нечетная четная Нули функции x=??k,k∈ℤ x=??/2+??k,k∈ℤ Промежутки знакопостоянства y(x)>0 x∈(2??k;??+2??k) x∈(-??/2+??k;??/2+??k)k∈ℤ y(x)
Cлайд 18
Cлайд 19
