X
Код презентации скопируйте его
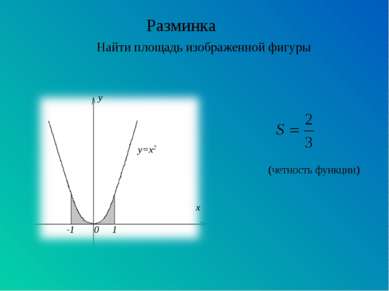
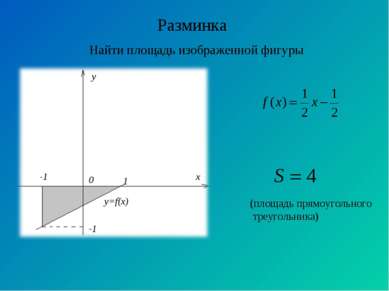
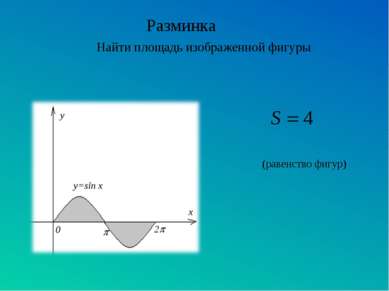
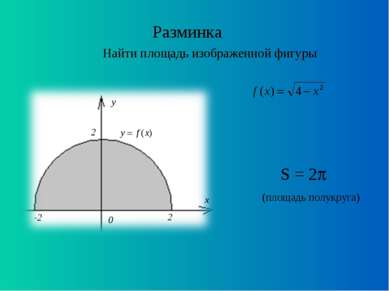
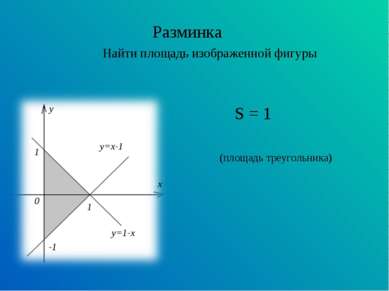
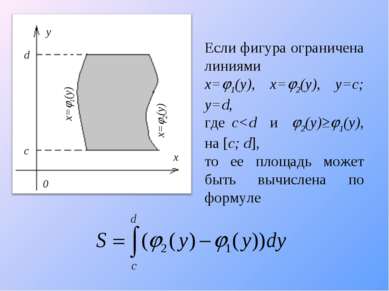
Вычисление площадей плоских фигур
Скачать эту презентацию
![Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y](https://bigslide.ru/images/18/17739/831/img1.jpg "Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y")
![y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры](https://bigslide.ru/images/18/17739/831/img2.jpg "y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры")
Презентация на тему Вычисление площадей плоских фигур
Скачать эту презентациюCлайд 1
Республика Башкортостан г. Уфа МАОУ лицей № 155 Ивушкина Л. Д.
Cлайд 2
![Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y](https://bigslide.ru/images/18/17739/960/img1.jpg "Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y")
Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y
Cлайд 3
![y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры](https://bigslide.ru/images/18/17739/960/img2.jpg "y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры")
y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры
Cлайд 4
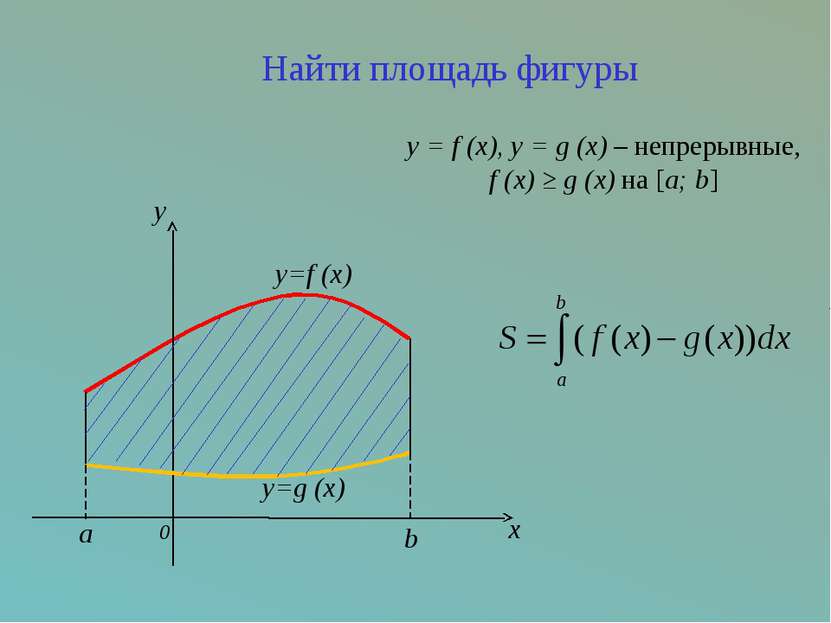
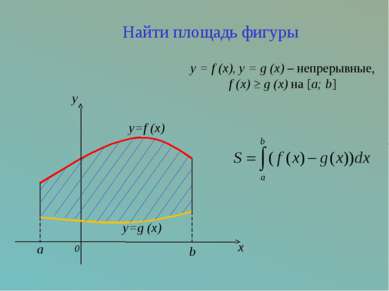0 y x y=g (x) y=f (x) b a y = f (x), y = g (x) – непрерывные, f (x) ≥ g (x) на [a; b] Найти площадь фигуры
Cлайд 5
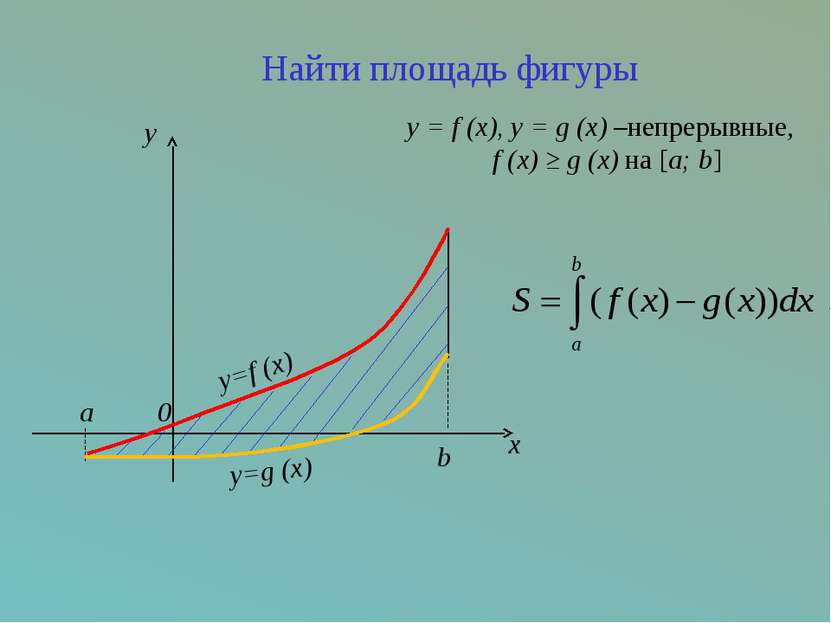
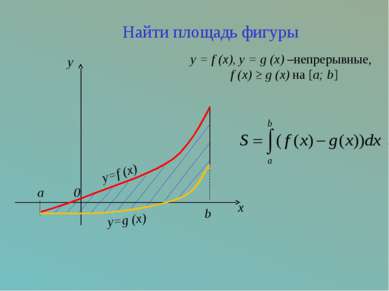y=f (x) a y=g (x) b 0 y x Найти площадь фигуры y = f (x), y = g (x) –непрерывные, f (x) ≥ g (x) на [a; b]
Cлайд 6
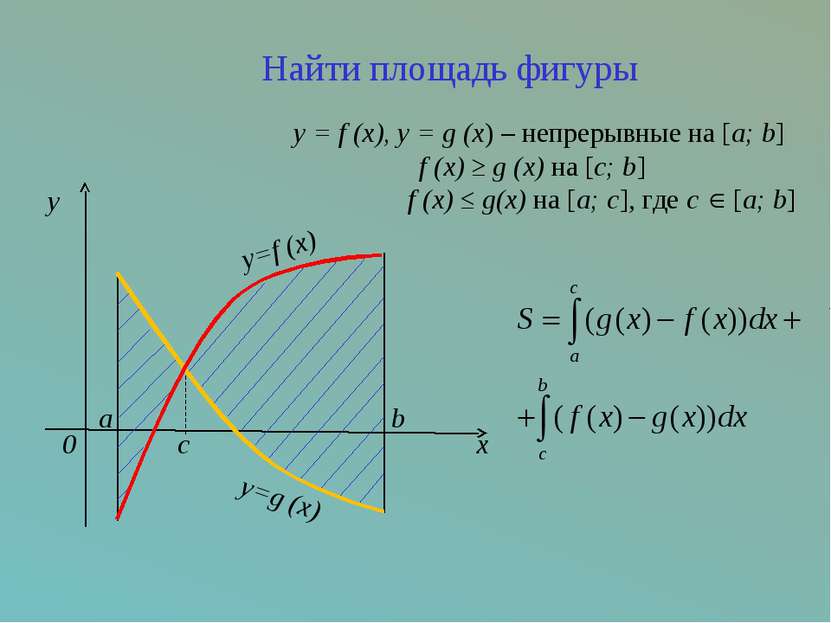
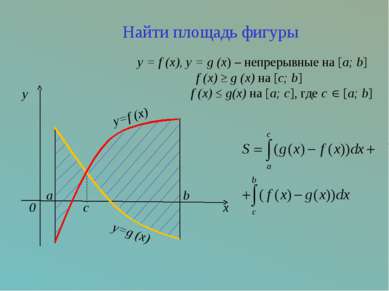c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f (x), y = g (x) – непрерывные на [a; b] f (x) ≥ g (x) на [c; b] f (x) ≤ g(x) на [a; c], где с [a; b]
Cлайд 7
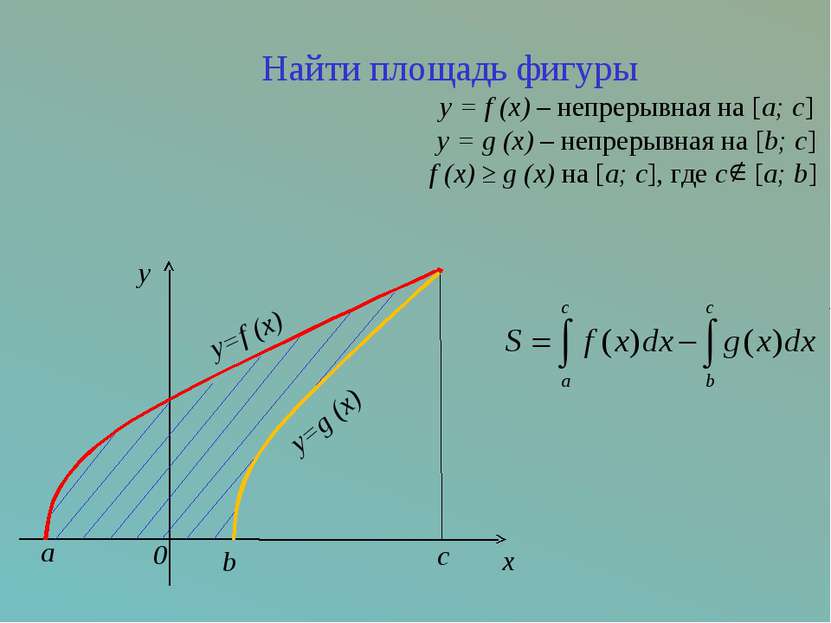
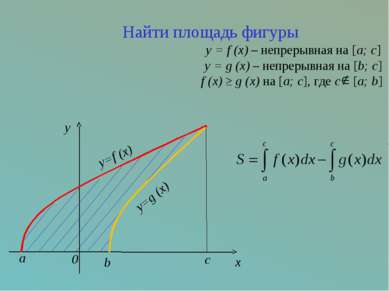c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f (x) – непрерывная на [a; c] y = g (x) – непрерывная на [b; c] f (x) ≥ g (x) на [a; c], где с [a; b]
Cлайд 8
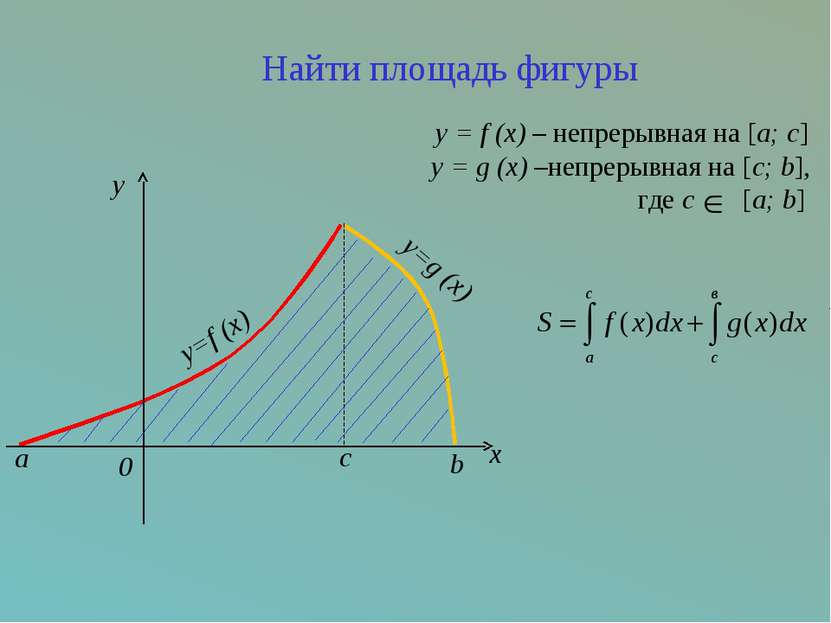
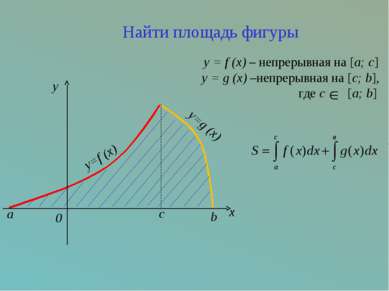c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f (x) – непрерывная на [a; c] y = g (x) –непрерывная на [c; b], где с [a; b]
Cлайд 9
(четность функции) Разминка Найти площадь изображенной фигуры
Cлайд 10
Разминка Найти площадь изображенной фигуры (площадь прямоугольного треугольника)
Cлайд 11
Разминка Найти площадь изображенной фигуры (равенство фигур)
Cлайд 12
Разминка Найти площадь изображенной фигуры S = 2 (площадь полукруга)
Cлайд 13
Разминка Найти площадь изображенной фигуры S = 1 (площадь треугольника)
Cлайд 14
Задачи 1) Найти площадь фигуры, ограниченной линиями
Cлайд 15
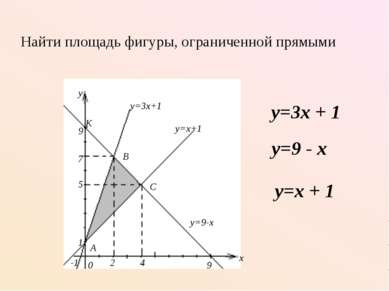
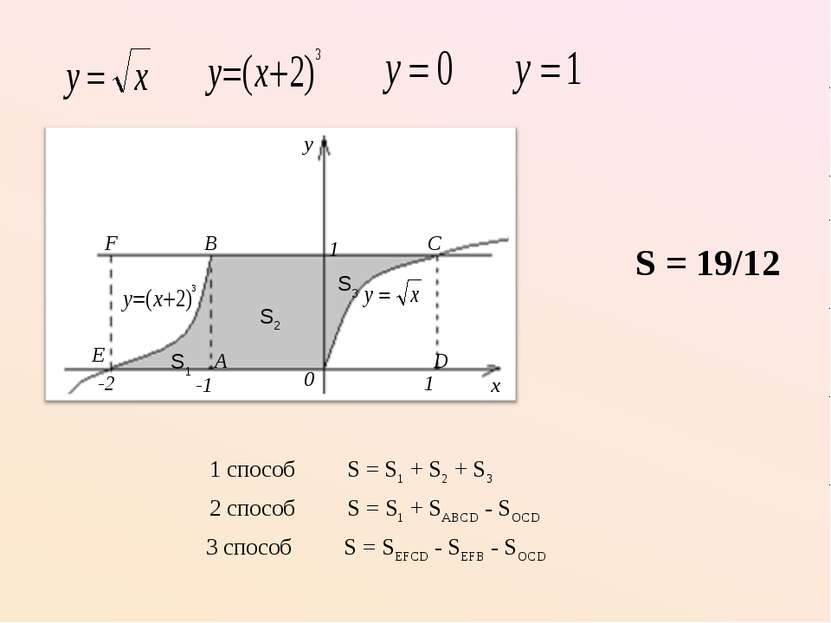
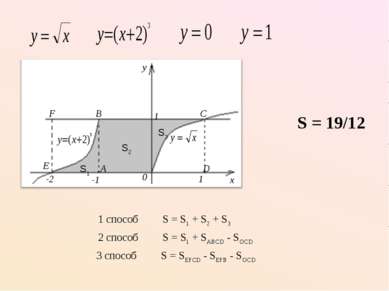1 способ S = S1 + S2 + S3 S = 19/12 2 способ S = S1 + SABCD - SOCD 3 способ S = SEFCD - SEFB - SOCD S1 S2 S3
Cлайд 16
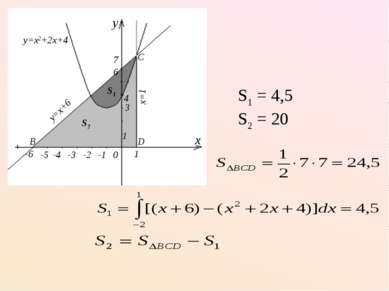
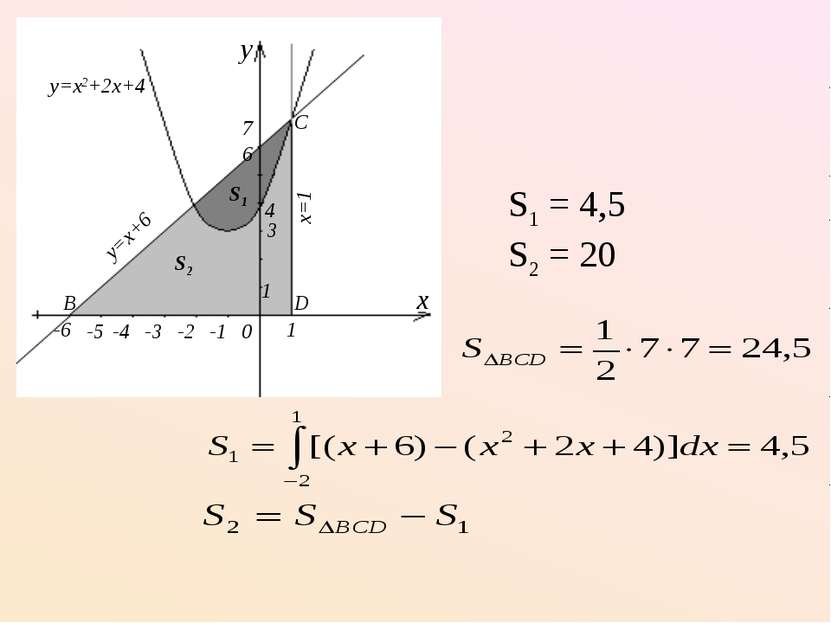
2) Фигура, ограниченная линиями y=x+6, x=1, y=0, делится параболой y=x2 + 2x + 4 на две части. Найти площадь каждой части.
Cлайд 17
S1 = 4,5 S2 = 20 1
Cлайд 18
Найти площадь фигуры, ограниченной прямыми y=3x + 1 y=9 - x y=x + 1
Cлайд 19
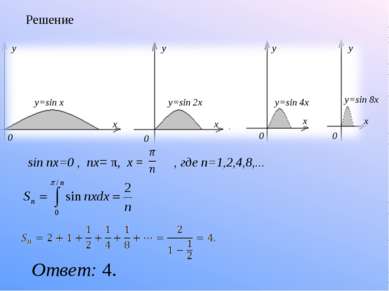
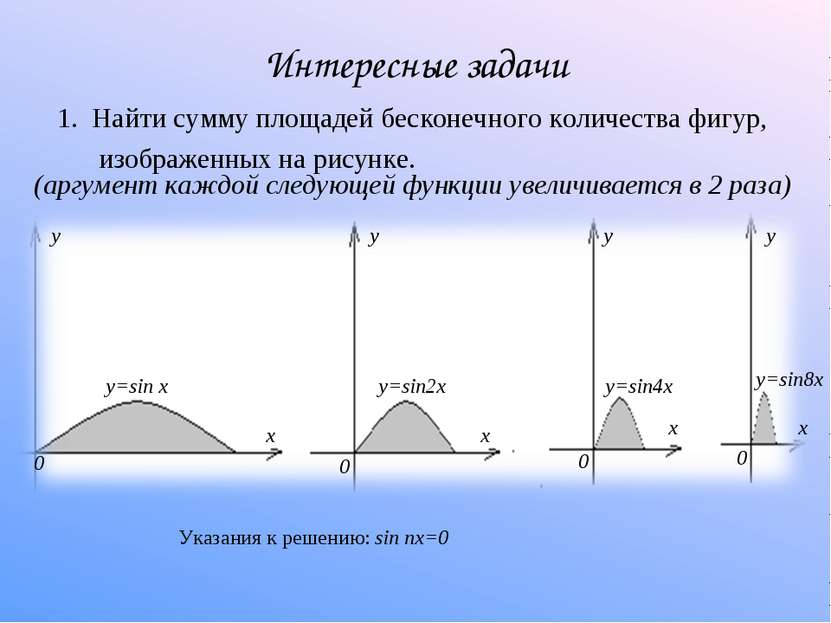
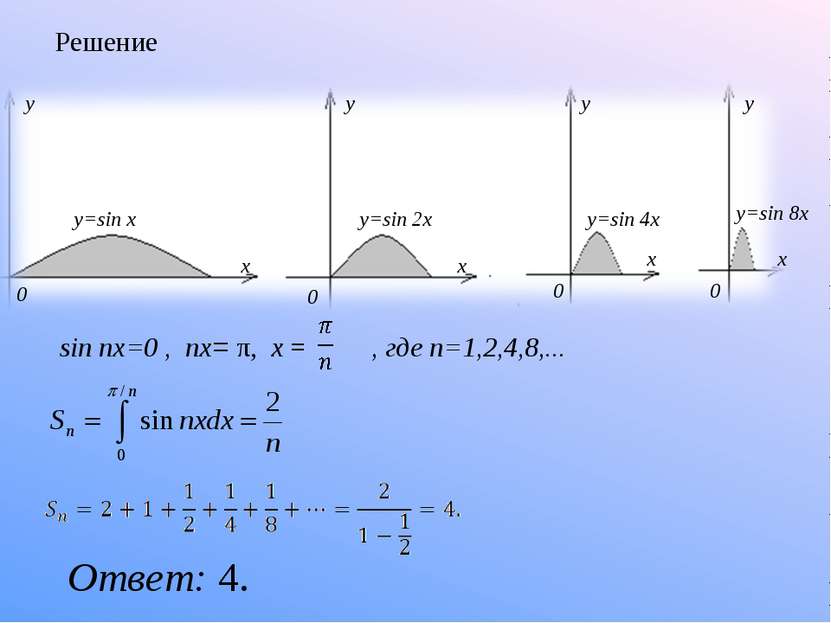
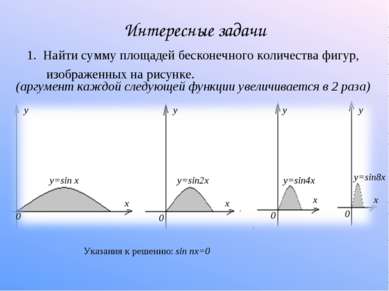Интересные задачи 1. Найти сумму площадей бесконечного количества фигур, изображенных на рисунке. (аргумент каждой следующей функции увеличивается в 2 раза) Указания к решению: sin nx=0
Cлайд 20
Ответ: 4. , где n=1,2,4,8,... sin nx=0 , nx= π, x = Решение
Cлайд 21
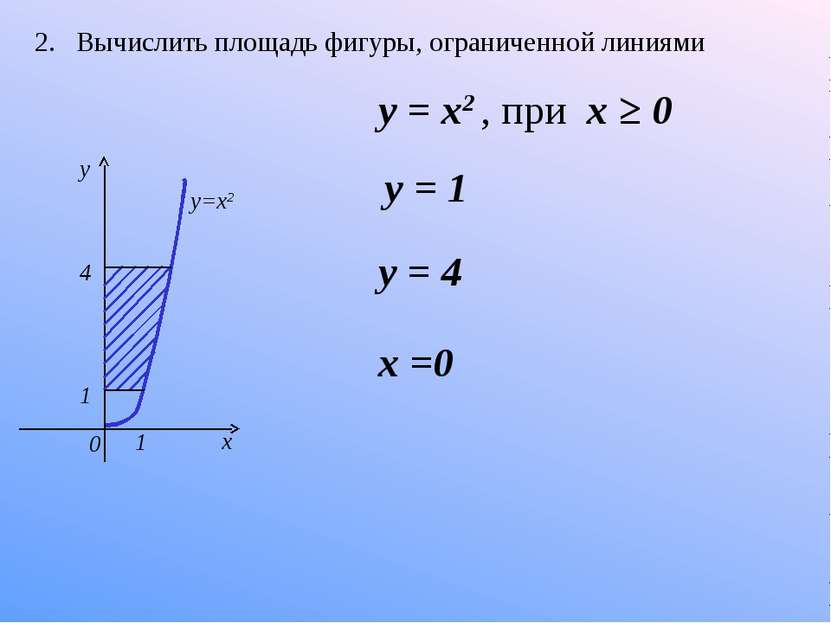
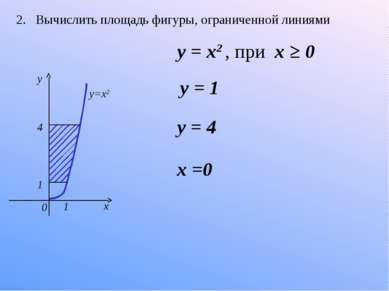2. Вычислить площадь фигуры, ограниченной линиями 1 1 4 0 x y y=x2 y = 1 y = 4 x =0 у = x2 , при x ≥ 0
Cлайд 22
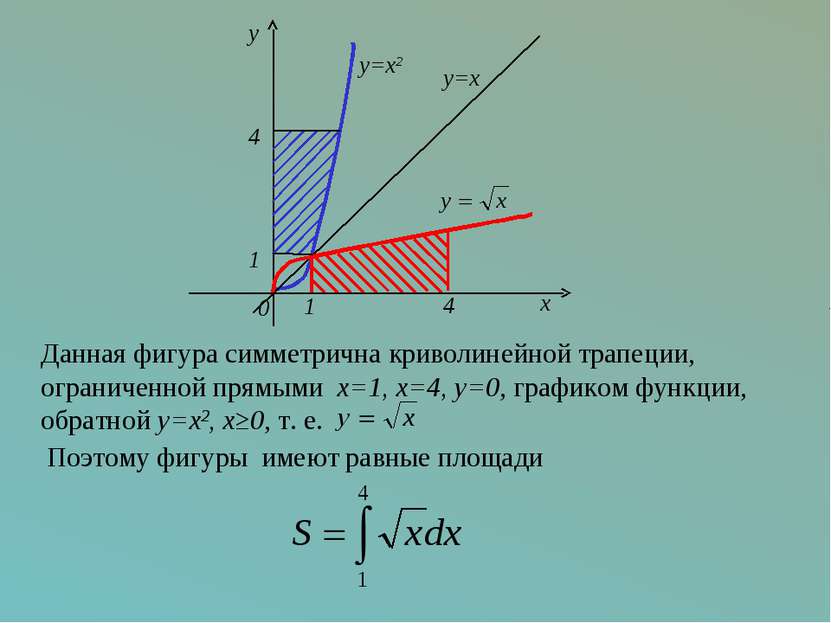
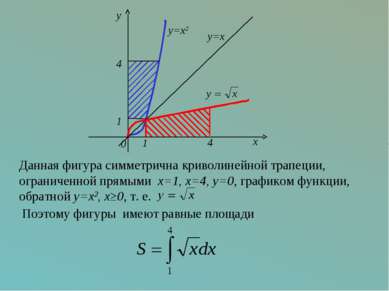Данная фигура симметрична криволинейной трапеции, ограниченной прямыми x=1, x=4, y=0, графиком функции, обратной y=x2, x≥0, т. е. Поэтому фигуры 1 4 1 4 0 x y y=x y=x2 имеют равные площади
Cлайд 23
Если фигура ограничена линиями x= 1(y), x= 2(y), y=c; y=d, где c
Cлайд 24
Используемая литература Алимов Ш.А. и др. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений.2002г. Звавич Л.И., Рязановский А.Р., Поташник А.М. Сборник задач по алгебре и математическому анализу для 10-11 кл. Вып.1 «Интеграл и площадь» 1996г. Галицкий М.Л. и др. Углубленное изучение алгебры и математического анализа. 10-11.Пособие для учителя. 1997г.
