Вычисление объемов пространственных тел с помощью интеграла

Скачать эту презентацию

Получить код Увеличить

Вычисление объемов пространственных тел с помощью интеграла. Воробьев Леонид ...

Немного теории. Чтобы получить представление об общем методе вычисления объем...

Немного теории. H x x С точки зрения геометрии мы построили сечения пространс...

Немного теории (базовые классы могут пропустить). H x x Если принять число ра...

I. Объем прямоугольного параллелепипеда с высотой H и площадью основания S. x...

II. Объем прямой призмы с высотой H и площадью основания S. x x [0;H] H 0 Пло...

III. Объем n-угольной прямой призмы с высотой H и площадью основания S. x x [...

IV. Объем наклонной призмы с высотой H и площадью основания S. Площадь сечени...

V. Объем треугольной пирамиды с высотой H и площадью основания S. H x x [0;H]...

VI. Объем n-угольной пирамиды с высотой H и площадью основания S. H x Площадь...

VIII. Объем цилиндра с высотой H и площадью основания S. x x [0;H] H 0 x Площ...

IX. Объем конуса с высотой H и площадью основания S. x x [0;H] H x Площадь се...

XI. Объем шара с радиусом R. Найдем объем полушария, как бесконечную интеграл...

XII. Объем шарового сегмента. Вывод объема шарового сегмента с высотой h и ра...

1 18

Презентация на тему Вычисление объемов пространственных тел с помощью интеграла

Скачать эту презентацию

Cлайд 1

Вычисление объемов пространственных тел с помощью интеграла. Воробьев Леонид Альбертович, г.Минск

Cлайд 2

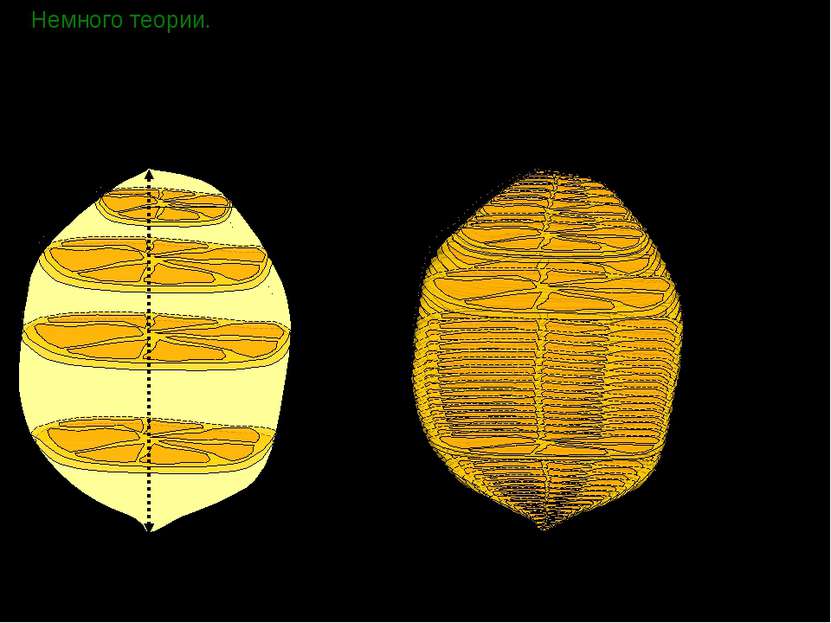
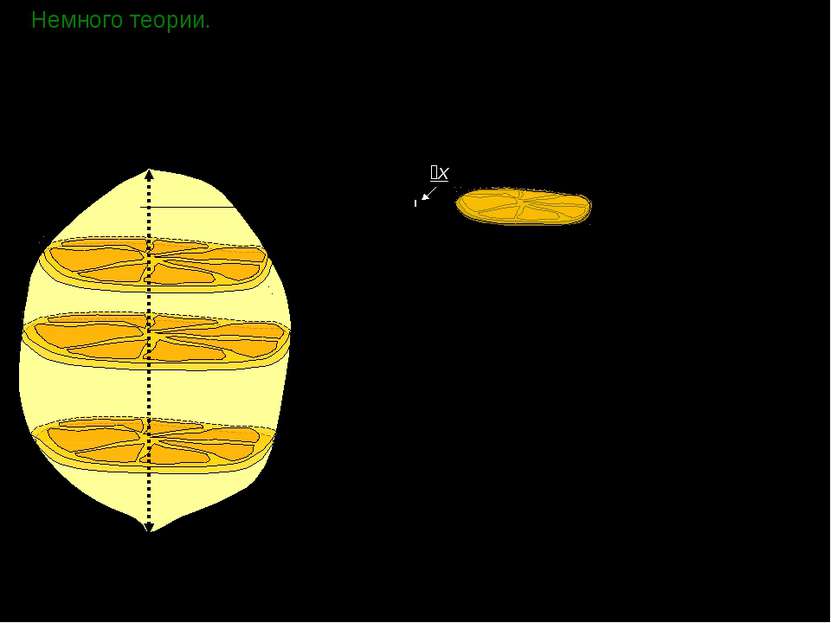
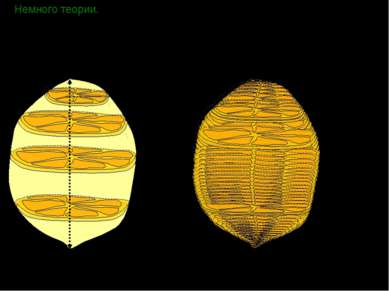Немного теории. Чтобы получить представление об общем методе вычисления объемов различных пространственных фигур, попробуем найти объем лимона. Ни на одно из тел, изучаемых в школе (призма, пирамида, шар, конус и т.д.), лимон не похож. Однако, мы можем поступить как все хозяйки – разрезать лимон на тонкие ломтики, размер которых зависит от расстояния x, причем x [0;H]. H x Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.

Cлайд 3

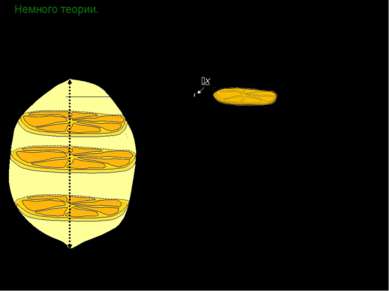Немного теории. H x x С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями, перпендикулярными оси фигуры; причем, если принять число разбиений бесконечно большим числом (n→ ), то: Проще говоря, при бесконечном числе разбиений каждый ломтик «вырождается» в плоское сечение и объем лимона равен бесконечной интегральной сумме площадей таких сечений, зависящих от расстояния x, т.е. где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x [0;H]. Sсеч.

Cлайд 4

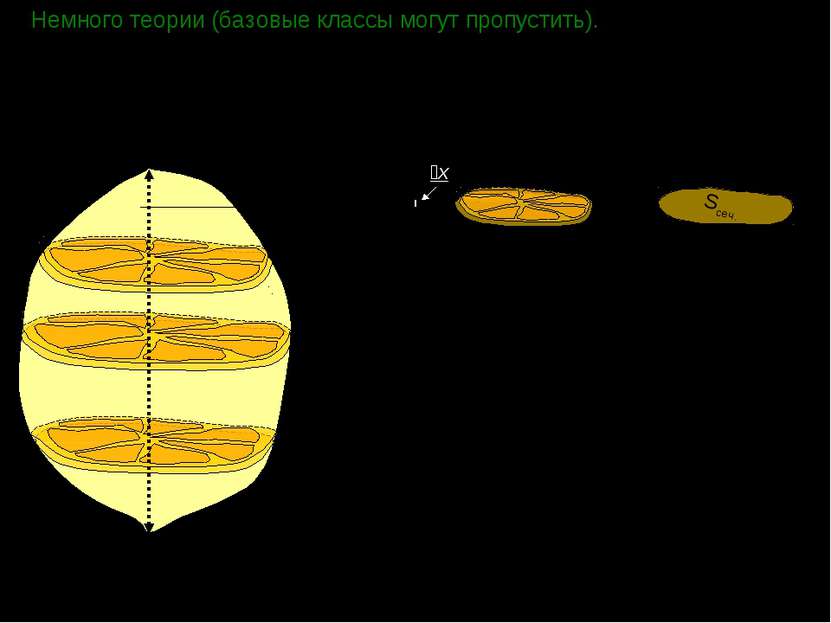
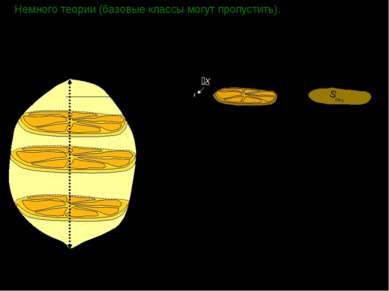Немного теории (базовые классы могут пропустить). H x x Если принять число разбиений бесконечно большим числом (n→ ), то: где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x [0;H]. Sсеч.

Cлайд 5

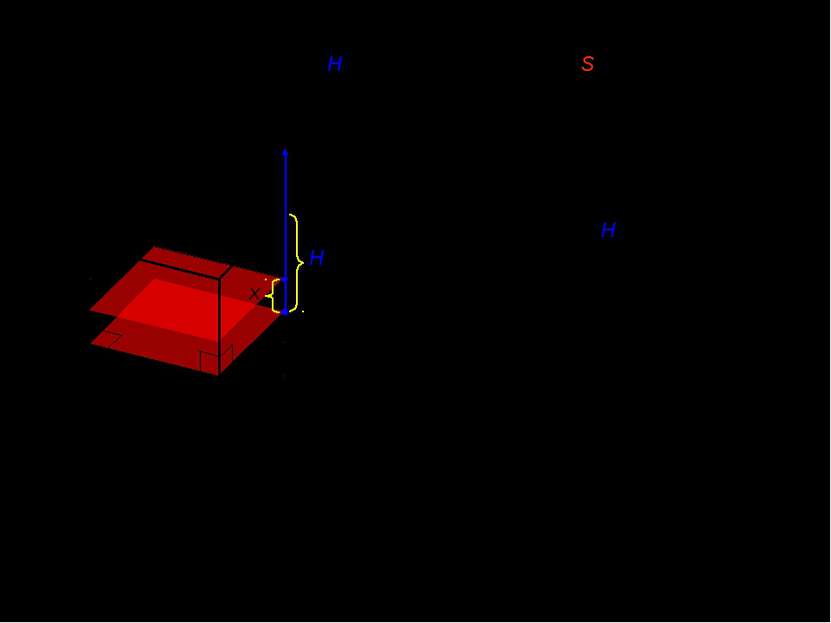
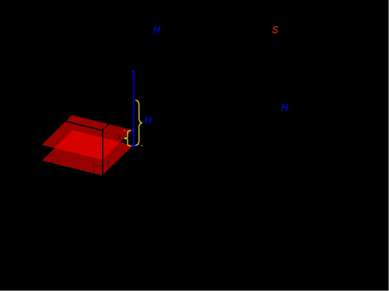I. Объем прямоугольного параллелепипеда с высотой H и площадью основания S. x H x [0;H] 0 Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания. x

Cлайд 6

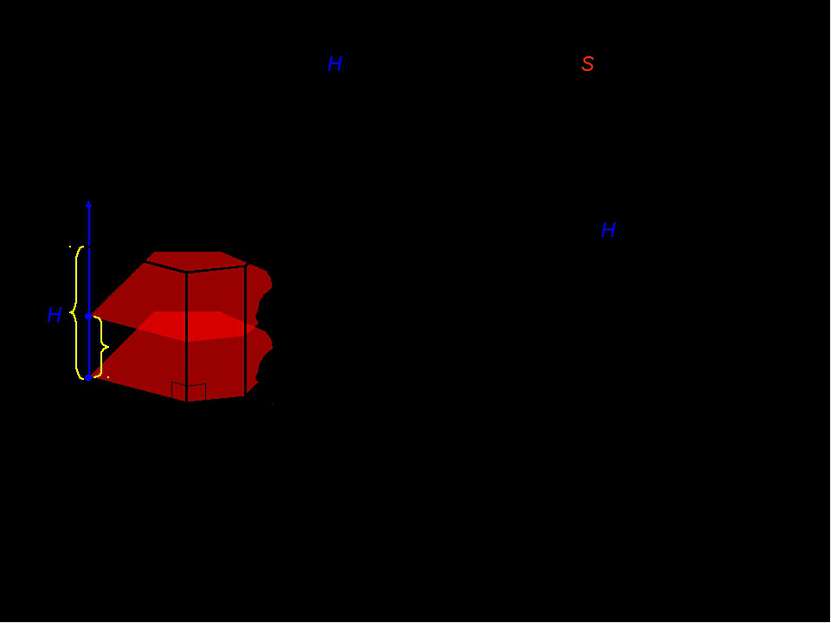
II. Объем прямой призмы с высотой H и площадью основания S. x x [0;H] H 0 Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания. x

Cлайд 7

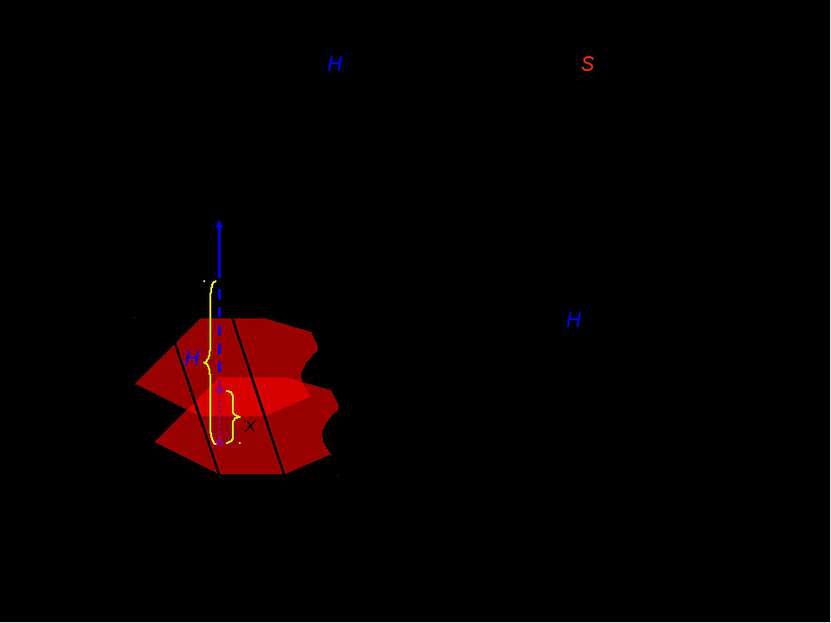
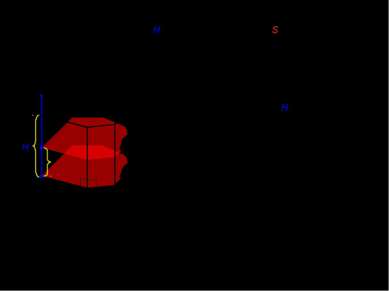III. Объем n-угольной прямой призмы с высотой H и площадью основания S. x x [0;H] H 0 Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания. x

Cлайд 8

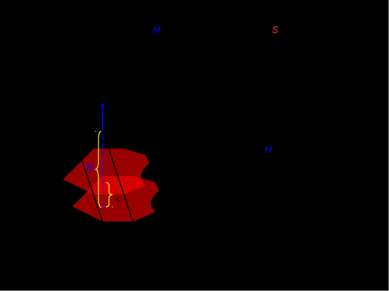IV. Объем наклонной призмы с высотой H и площадью основания S. Площадь сечения, перпендикулярного высоте, не изменяется в любой точке отрезка от 0 до H и равна площади основания. x H x [0;H] 0 x

Cлайд 9

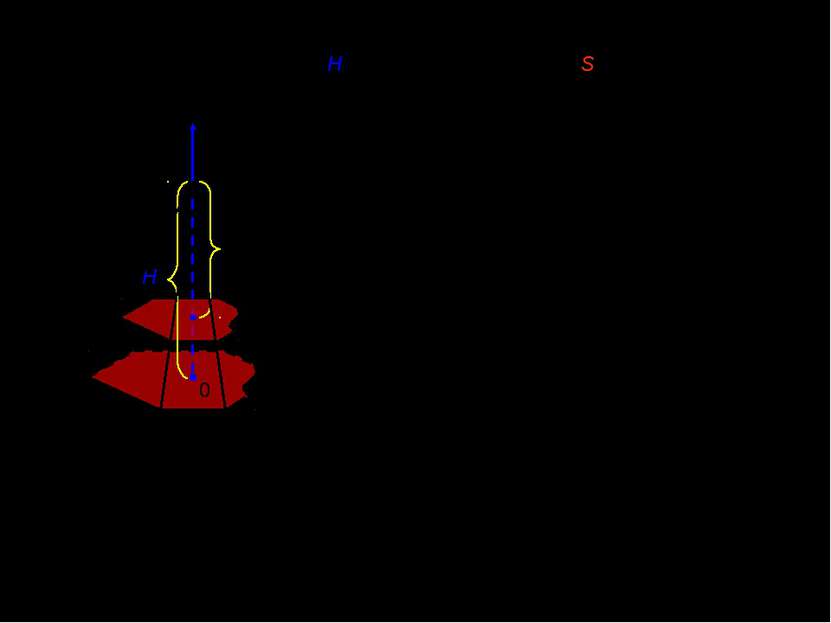
V. Объем треугольной пирамиды с высотой H и площадью основания S. H x x [0;H] x Площадь сечения изменяется в зависимости от расстояния x, причем отношение площади основания к площади сечения равно квадрату коэффициента подобия соответственных треугольников, т.е.: 0

Cлайд 10

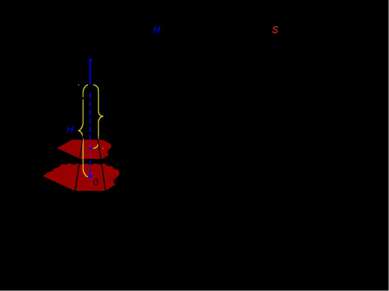VI. Объем n-угольной пирамиды с высотой H и площадью основания S. H x Площадь сечения изменяется в зависимости от расстояния x, причем отношение площади основания к площади сечения равно квадрату коэффициента подобия соответственных n-угольников, т.е.: x x [0;H] 0

Cлайд 11

VII. Объем усеченной пирамиды. текст

Cлайд 12

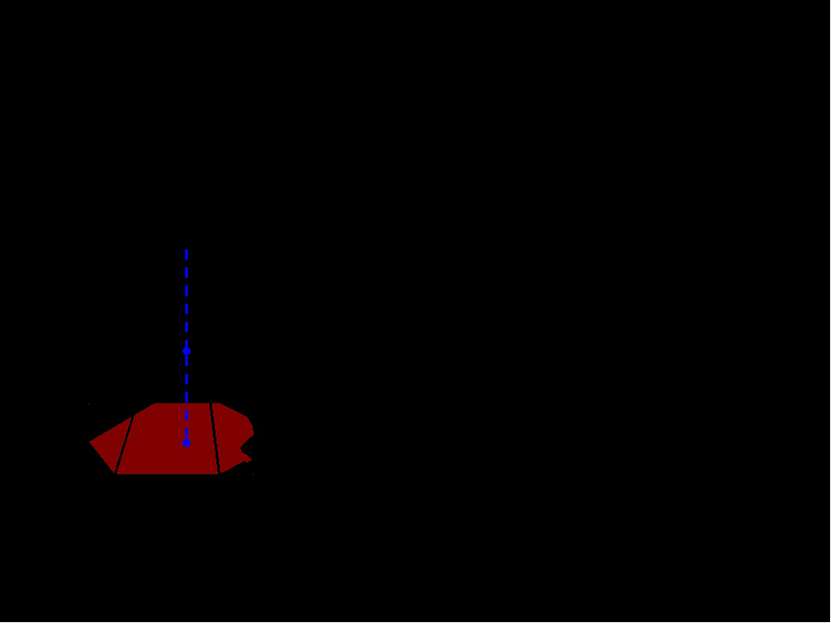
VIII. Объем цилиндра с высотой H и площадью основания S. x x [0;H] H 0 x Площадь сечения не изменяется в любой точке отрезка от 0 до H и равна площади основания.

Cлайд 13

IX. Объем конуса с высотой H и площадью основания S. x x [0;H] H x Площадь сечения изменяется в зависимости от расстояния x, причем отношение площади основания к площади сечения равно квадрату коэффициента подобия соответственных кругов, т.е.: 0

Cлайд 14

X. Объем усеченного конуса. текст

Cлайд 15

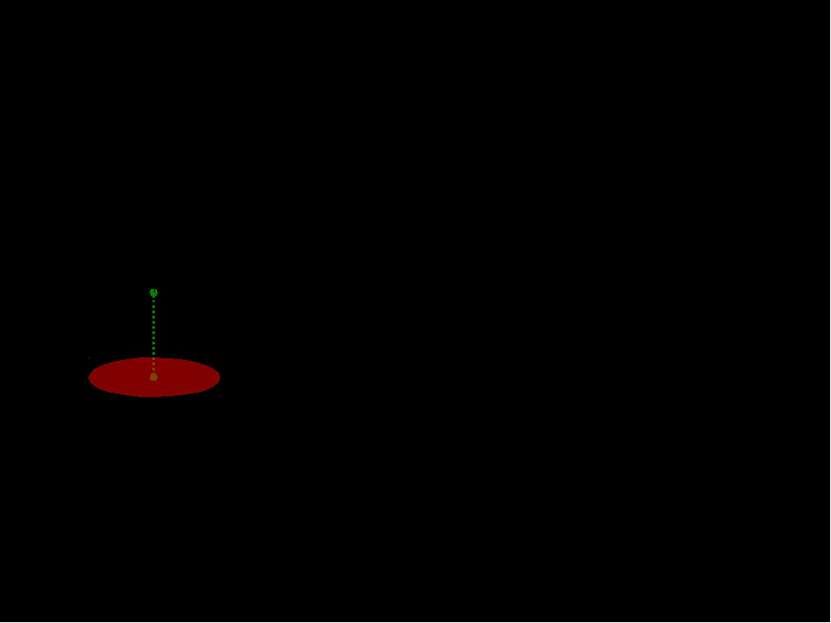
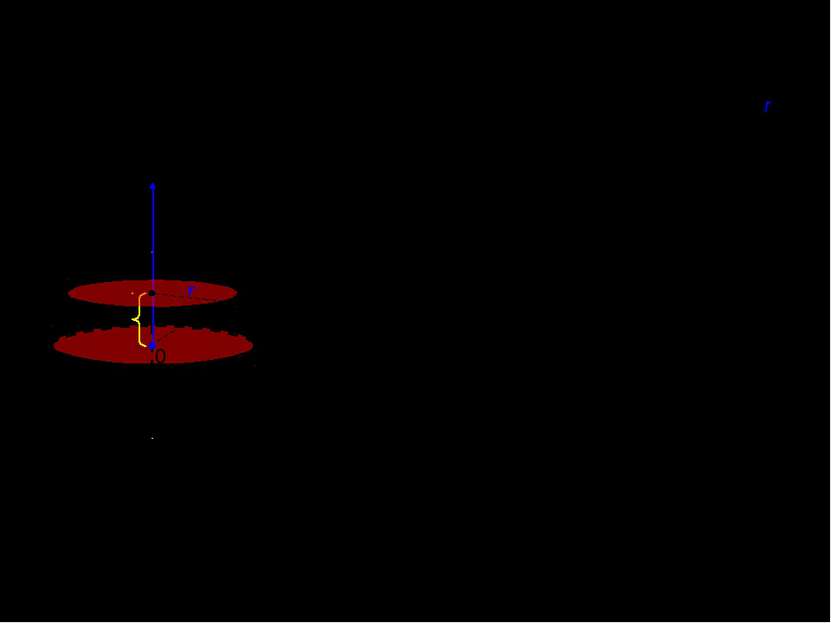
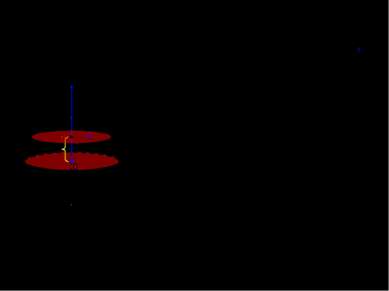XI. Объем шара с радиусом R. Найдем объем полушария, как бесконечную интегральную сумму площадей сечения с радиусом r, где: R x Значит, объем всего шара равен: x 0 r

Cлайд 16

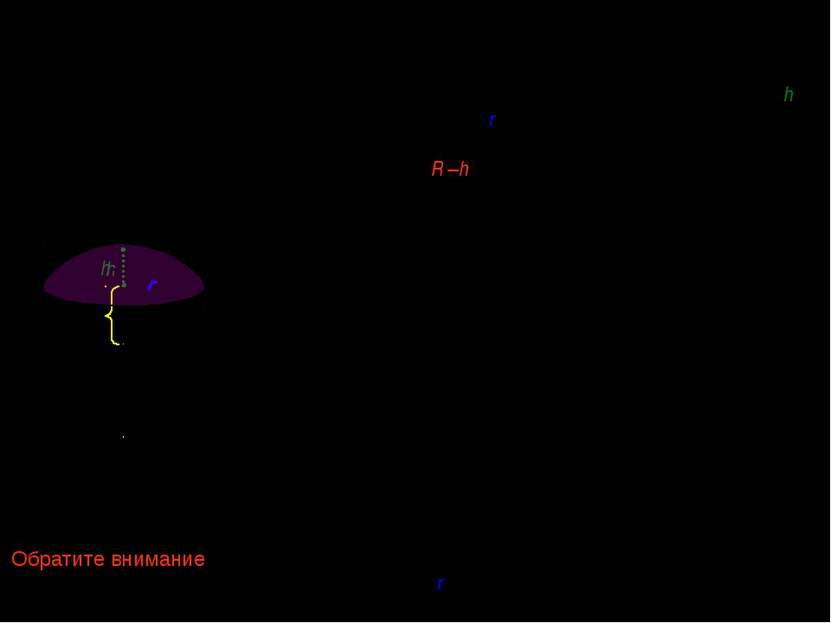
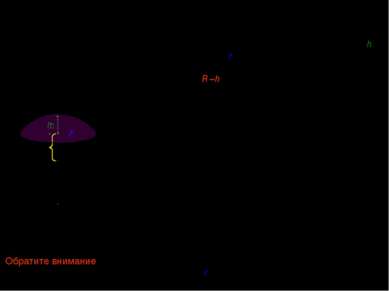XII. Объем шарового сегмента. Вывод объема шарового сегмента с высотой h и радиусом основания r отличается от вывода объема полушария нижним пределом интегрирования. В данном случае он равен R –h : r R h x Обратите внимание, что в формуле объема шарового сегмента участвует радиус шара (R), а не радиус основания сегмента (r)!

Cлайд 17