X
Код презентации скопируйте его
Многогранники: виды задач и методы их решения (типовые задания С2) - 1
Скачать эту презентацию
Презентация на тему Многогранники: виды задач и методы их решения (типовые задания С2) - 1
Скачать эту презентациюCлайд 1
(типовые задания С2) - 1 Многогранники: виды задач и методы их решения Методическая разработка Амачкиной А.А. МОУ СОШ №12, г. Балашиха, Московской области.
Cлайд 2
Расстояние между точками A и B можно вычислить: 1) как длину отрезка AB , если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон; 2) по формуле 3) по формуле 1.1. Расстояние между двумя точками
Cлайд 3
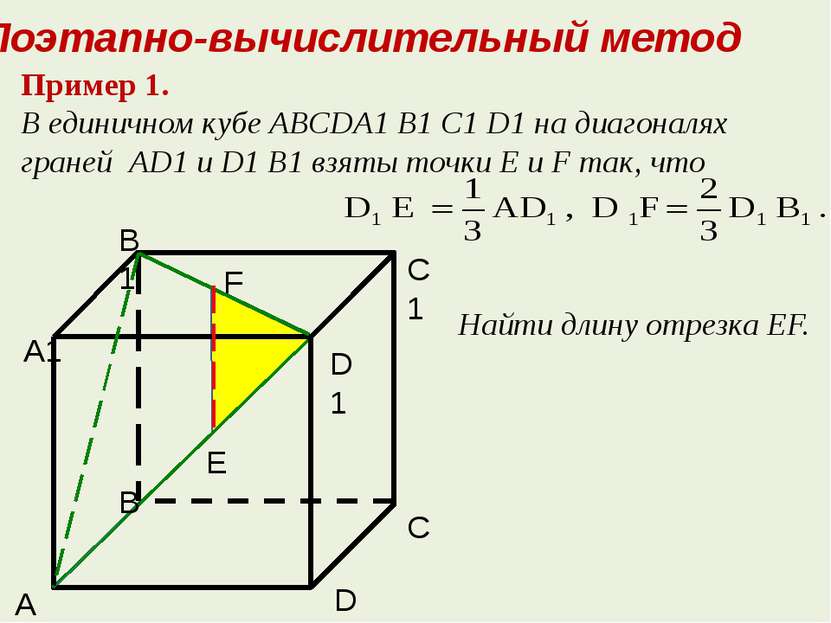
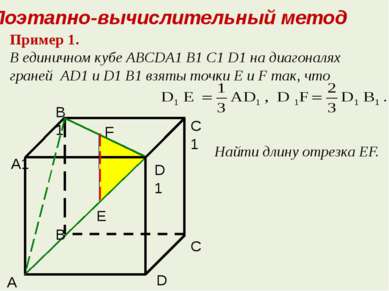Пример 1. В единичном кубе ABCDA1 B1 C1 D1 на диагоналях граней AD1 и D1 B1 взяты точки Е и F так, что Найти длину отрезка EF. Поэтапно-вычислительный метод
Cлайд 4
(треугольник AB1 D1 является равносторонним). Имеем
Cлайд 5
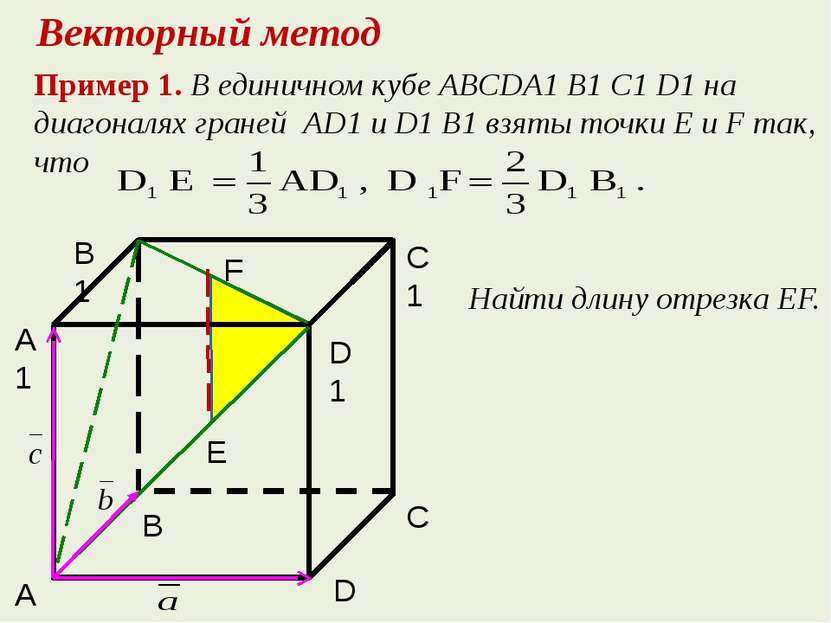
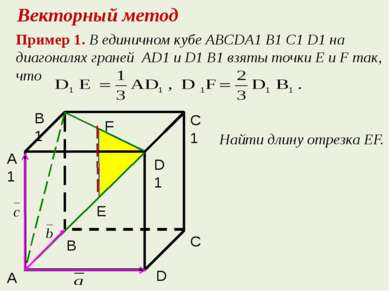Пример 1. В единичном кубе ABCDA1 B1 C1 D1 на диагоналях граней AD1 и D1 B1 взяты точки Е и F так, что Найти длину отрезка EF. Векторный метод А А1 В1 В Е D С D1 С1 F
Cлайд 6
Решение. Пусть
Cлайд 7
Замечание.
Cлайд 8
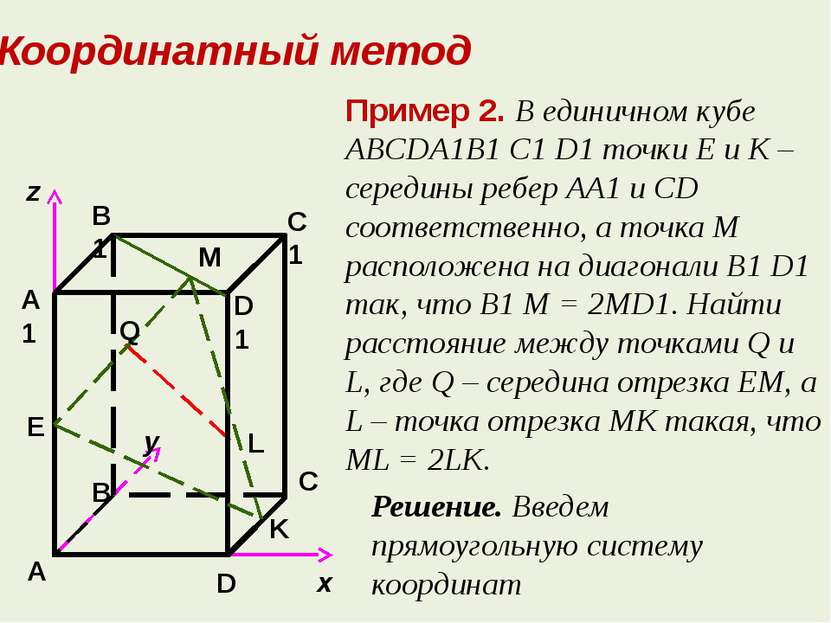
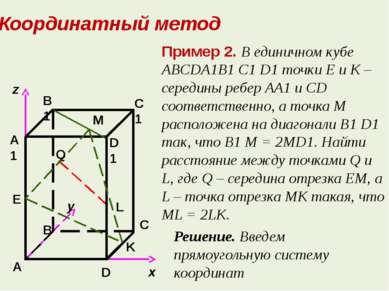Решение. Введем прямоугольную систему координат Пример 2. В единичном кубе ABCDA1B1 C1 D1 точки E и K – середины ребер AA1 и CD соответственно, а точка M расположена на диагонали B1 D1 так, что B1 M = 2MD1. Найти расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML = 2LK. Координатный метод А E D C K x z Q M L А1 B1 C1 D1 B y
Cлайд 9
Для нахождения координат точки М используем формулу координат точки (опорная задача 1), делящей отрезок B1 D1 в отношении 2:1. Имеем Тогда Аналогично получим координаты точки L, делящей отрезок MK в отношении 2:1. Имеем
Cлайд 10
Координаты точки Q равны полусуммам соответствующих координат точек E и М, поэтому
Cлайд 11
Используемая литература: Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2) Корянов А. Г., г. Брянск, akoryanov@mail.ru Прокофьев А.А., г. Москва, aaprokof@yandex.ru
