X
Код презентации скопируйте его
Применение производной для решения задач в формате ЕГЭ
Скачать эту презентациюПрезентация на тему Применение производной для решения задач в формате ЕГЭ
Скачать эту презентациюCлайд 1
 Муниципальное общеобразовательное учреждение Нурлатская средняя общеобразовательная школа №1 Нурлатского муниципального района Республики Татарстан Применение производной для решения задач в формате ЕГЭ Урок для 11 класса подготовила учитель математики Муртазина Римма Хамдямовна 2010-2011 уч. год
Муниципальное общеобразовательное учреждение Нурлатская средняя общеобразовательная школа №1 Нурлатского муниципального района Республики Татарстан Применение производной для решения задач в формате ЕГЭ Урок для 11 класса подготовила учитель математики Муртазина Римма Хамдямовна 2010-2011 уч. год
Cлайд 2
 Цель: научить решать правильно задания ЕГЭ по разделу «Производная», для реализации которой были поставлены следующие задача. Задача: показать возможности графика производной функции (нахождение наибольшего и наименьшего значения функции, экстремума функции, углового коэффициента, значение производной функции в точке касания и тангенс угла наклона).
Цель: научить решать правильно задания ЕГЭ по разделу «Производная», для реализации которой были поставлены следующие задача. Задача: показать возможности графика производной функции (нахождение наибольшего и наименьшего значения функции, экстремума функции, углового коэффициента, значение производной функции в точке касания и тангенс угла наклона).
Cлайд 3
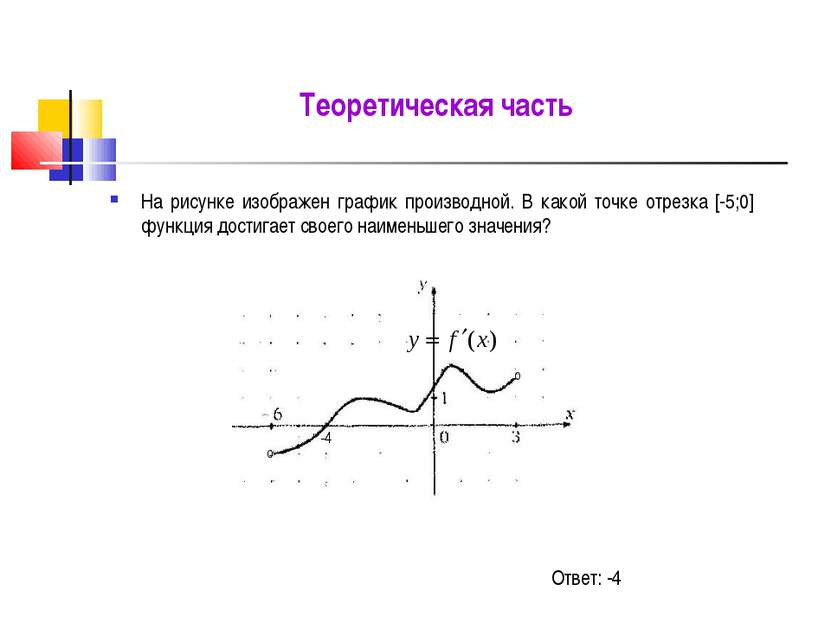
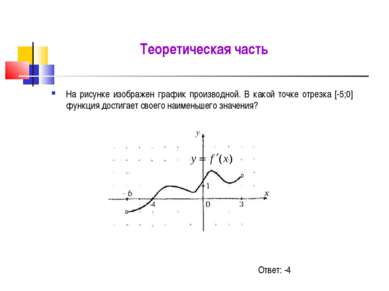 Теоретическая часть На рисунке изображен график производной. В какой точке отрезка [-5;0] функция достигает своего наименьшего значения? -4 0 0 Ответ: -4
Теоретическая часть На рисунке изображен график производной. В какой точке отрезка [-5;0] функция достигает своего наименьшего значения? -4 0 0 Ответ: -4
Cлайд 4
![Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график прои... Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график прои...](https://bigslide.ru/images/1/171/389/img3.jpg) Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график производной функции .В какой точке отрезка функция принимает наименьшее значение? Ответ: 3
Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график производной функции .В какой точке отрезка функция принимает наименьшее значение? Ответ: 3
Cлайд 5
![Функция у=f(x) определена на отрезке [-3;5]. На рисунке изображен график прои... Функция у=f(x) определена на отрезке [-3;5]. На рисунке изображен график прои...](https://bigslide.ru/images/1/171/389/img4.jpg) Функция у=f(x) определена на отрезке [-3;5]. На рисунке изображен график производной функции .В какой точке отрезка функция принимает наибольшее значение? Ответ: 5
Функция у=f(x) определена на отрезке [-3;5]. На рисунке изображен график производной функции .В какой точке отрезка функция принимает наибольшее значение? Ответ: 5
Cлайд 6
![На рисунке изображен график производной. В какой точке отрезка [-1;4] функция... На рисунке изображен график производной. В какой точке отрезка [-1;4] функция...](https://bigslide.ru/images/1/171/389/img5.jpg) На рисунке изображен график производной. В какой точке отрезка [-1;4] функция достигает своего наибольшего значения? На рисунке изображен график производной. В какой точке отрезка (-5;2] функция достигает своего наименьшего значения? -1 4 -6 2 -5 -1 Ответ: 4 Ответ: 2
На рисунке изображен график производной. В какой точке отрезка [-1;4] функция достигает своего наибольшего значения? На рисунке изображен график производной. В какой точке отрезка (-5;2] функция достигает своего наименьшего значения? -1 4 -6 2 -5 -1 Ответ: 4 Ответ: 2
Cлайд 8
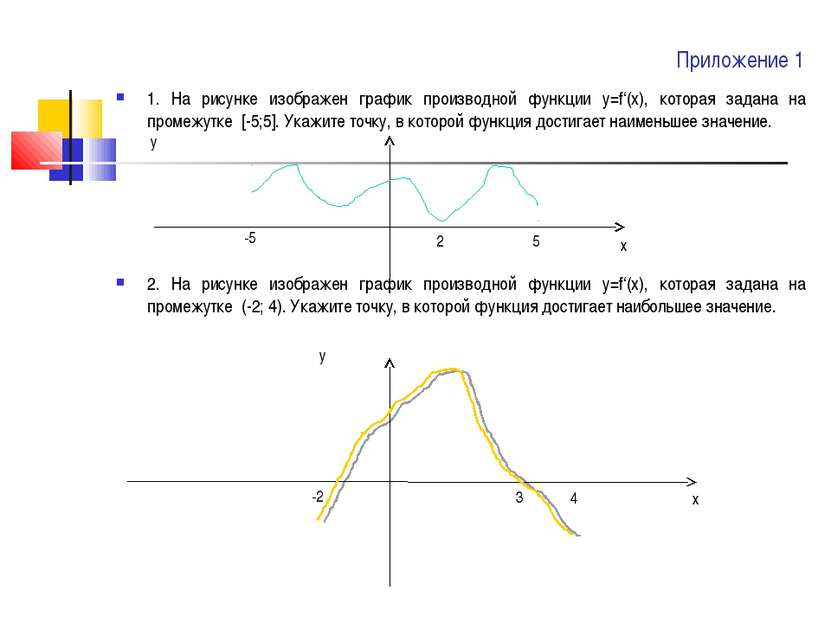
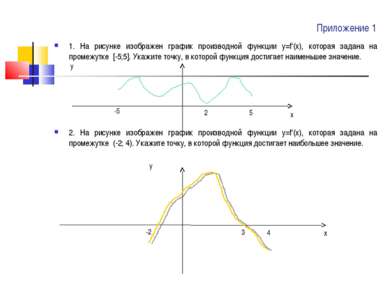 Приложение 1 1. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке [-5;5]. Укажите точку, в которой функция достигает наименьшее значение. у 2. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке (-2; 4). Укажите точку, в которой функция достигает наибольшее значение. у -5 5 2 -2 3 4 х х
Приложение 1 1. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке [-5;5]. Укажите точку, в которой функция достигает наименьшее значение. у 2. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке (-2; 4). Укажите точку, в которой функция достигает наибольшее значение. у -5 5 2 -2 3 4 х х
Cлайд 9
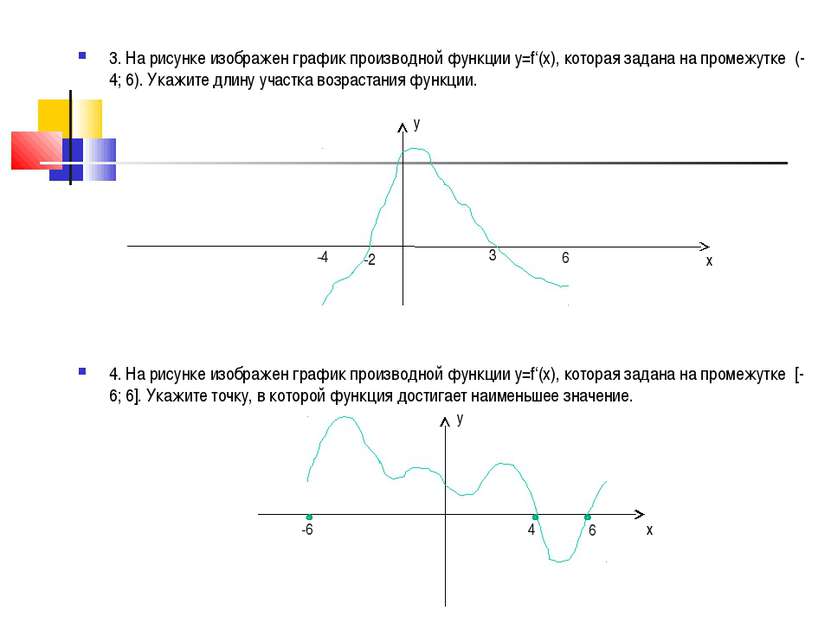
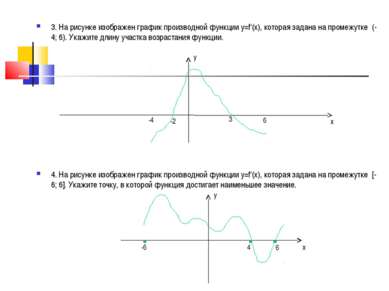 3. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке (-4; 6). Укажите длину участка возрастания функции. 4. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке [-6; 6]. Укажите точку, в которой функция достигает наименьшее значение. 1. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке [-5;5]. Укажите точку, в которой функция достигает наименьшее значение. у -6 4 6
3. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке (-4; 6). Укажите длину участка возрастания функции. 4. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке [-6; 6]. Укажите точку, в которой функция достигает наименьшее значение. 1. На рисунке изображен график производной функции у=f‘(x), которая задана на промежутке [-5;5]. Укажите точку, в которой функция достигает наименьшее значение. у -6 4 6
Cлайд 10
![Функция определена на отрезке [-4;7]. На рисунке изображен график её производ... Функция определена на отрезке [-4;7]. На рисунке изображен график её производ...](https://bigslide.ru/images/1/171/389/img9.jpg) Функция определена на отрезке [-4;7]. На рисунке изображен график её производной у= . Найдите число точек максимума этой функции на интервале (-3,5;6) На данном рисунке найдите точку минимума Ответ: 2 -2 3 5,5 + + _ _ Ответ: 3 Теоретическая часть
Функция определена на отрезке [-4;7]. На рисунке изображен график её производной у= . Найдите число точек максимума этой функции на интервале (-3,5;6) На данном рисунке найдите точку минимума Ответ: 2 -2 3 5,5 + + _ _ Ответ: 3 Теоретическая часть
Cлайд 12
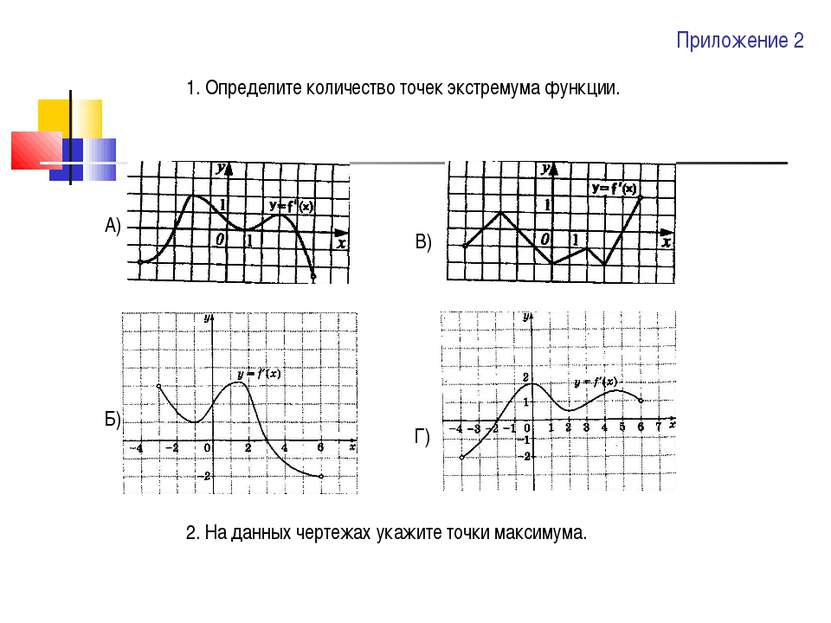
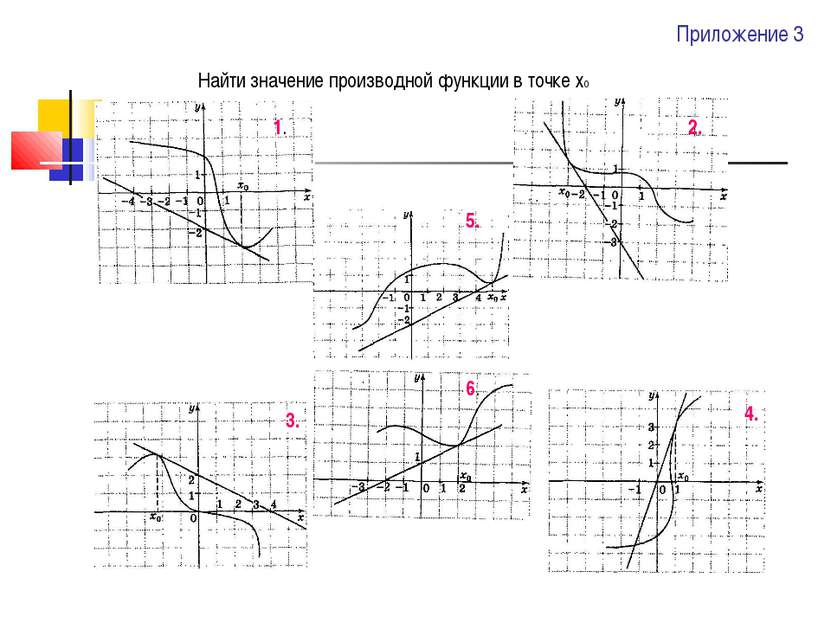
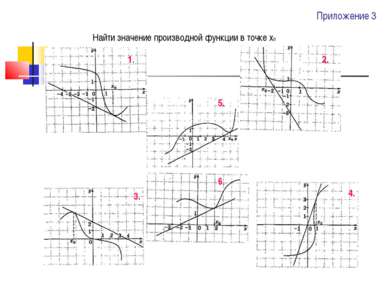
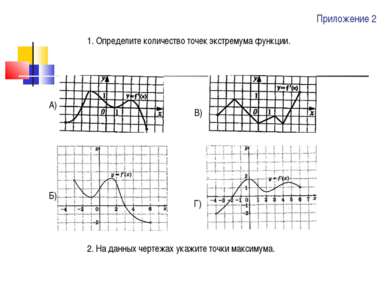 Приложение 2 1. Определите количество точек экстремума функции. 2. На данных чертежах укажите точки максимума. А) Б) В) Г)
Приложение 2 1. Определите количество точек экстремума функции. 2. На данных чертежах укажите точки максимума. А) Б) В) Г)
Cлайд 13
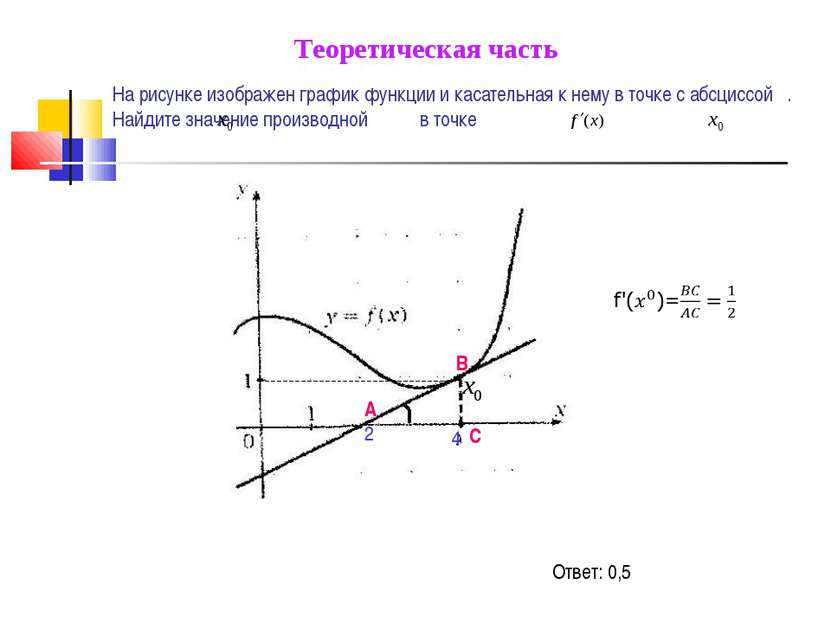
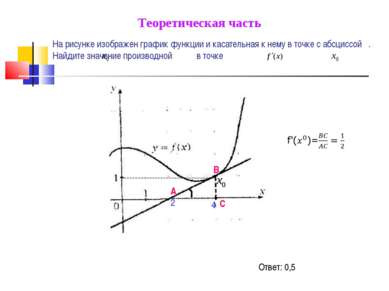 На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной в точке Ответ: 0,5 Теоретическая часть
На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной в точке Ответ: 0,5 Теоретическая часть
Cлайд 14
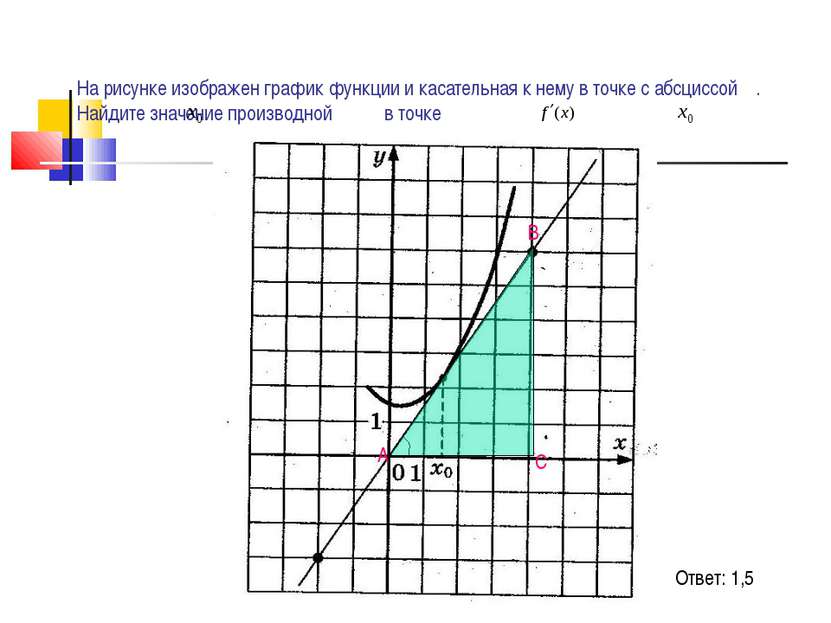
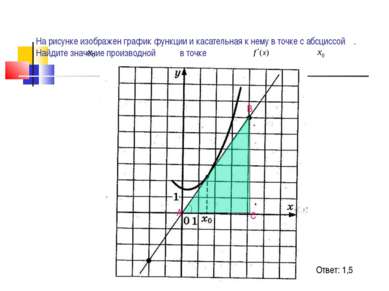 На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной в точке Ответ: 1,5
На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной в точке Ответ: 1,5
Cлайд 15
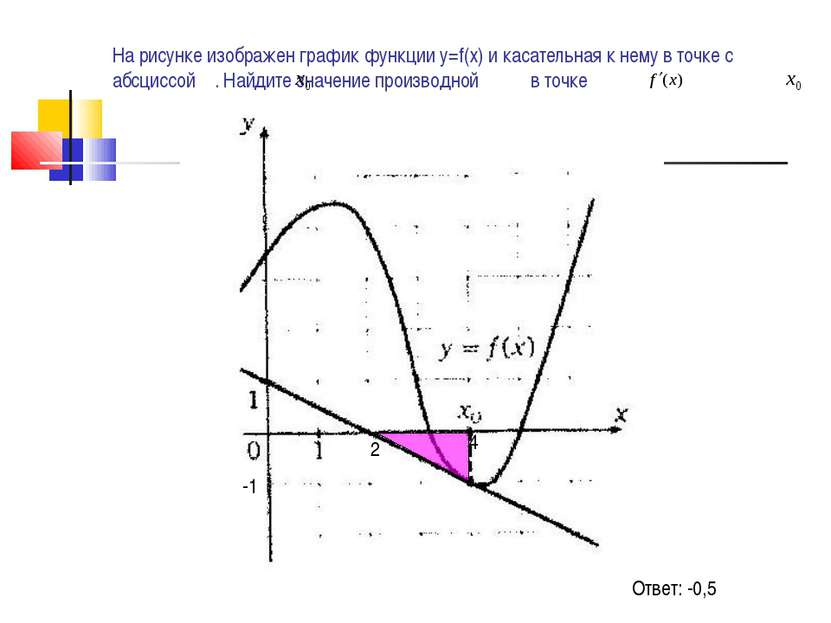
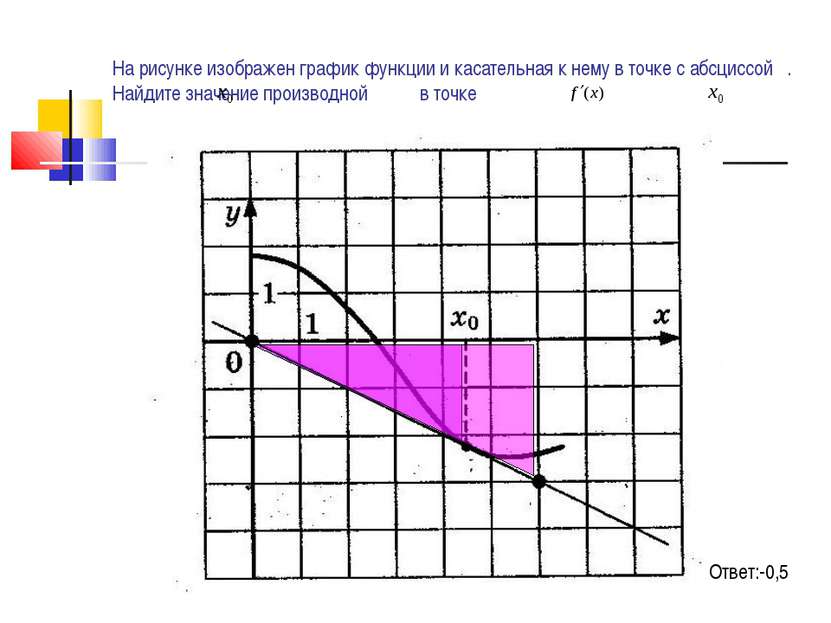
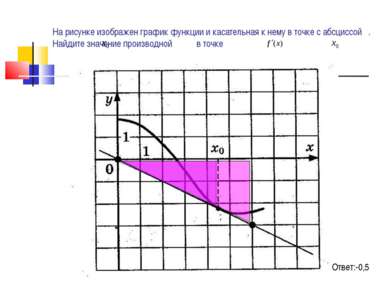
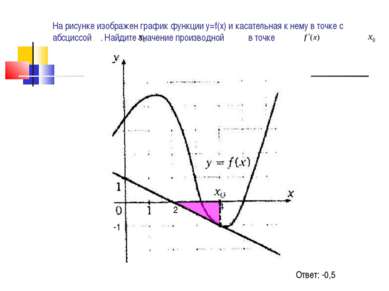 На рисунке изображен график функции у=f(х) и касательная к нему в точке с абсциссой . Найдите значение производной в точке Ответ: -0,5
На рисунке изображен график функции у=f(х) и касательная к нему в точке с абсциссой . Найдите значение производной в точке Ответ: -0,5



![Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график прои... Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график прои...](https://bigslide.ru/images/1/171/831/img3.jpg)
![Функция у=f(x) определена на отрезке [-3;5]. На рисунке изображен график прои... Функция у=f(x) определена на отрезке [-3;5]. На рисунке изображен график прои...](https://bigslide.ru/images/1/171/831/img4.jpg)
![На рисунке изображен график производной. В какой точке отрезка [-1;4] функция... На рисунке изображен график производной. В какой точке отрезка [-1;4] функция...](https://bigslide.ru/images/1/171/831/img5.jpg)

![Функция определена на отрезке [-4;7]. На рисунке изображен график её производ... Функция определена на отрезке [-4;7]. На рисунке изображен график её производ...](https://bigslide.ru/images/1/171/831/img9.jpg)