X
Код презентации скопируйте его
Линейная функция и её график
Скачать эту презентацию
Презентация на тему Линейная функция и её график
Скачать эту презентациюCлайд 1
Урок алгебры в 7 классе «Линейная функция и её график» Подготовила Татчин У.В. учитель математики МБОУ СОШ №3 город Сургут
Cлайд 2
Цель: формирование понятия «линейная функция», навыка построения её графика по алгоритму Задачи: Образовательные: - изучить определение линейной функции, - ввести и изучить алгоритм построения графика линейной функции, - отработать навык распознавания линейной функции по заданной формуле, графику, словесному описанию. Развивающие: - развивать зрительную память, математически грамотную речь, аккуратность, точность в построении, умение анализировать. Воспитательные: - воспитывать ответственное отношение к учебному труду, аккуратность, дисциплинированность, усидчивость. - формировать навыки самоконтроля и взаимоконтроля
Cлайд 3
План урока: I. Организационный момент II. Актуализация опорных знаний III. Изучение новой темы IV. Закрепление: устные упражнения, задачи на построение графиков V. Решение занимательных заданий VI. Подведение итога урока, запись домашнего задания VII. Рефлексия
Cлайд 4
I. Организационный момент Разгадав слова по горизонтали, вы узнаете ключевое слово 1. Точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время 2. Одна из координат точки 3. Зависимость одной переменной от другой, при которой каждому значению аргумента соответствует единственное значение зависимой переменной 4. Французский математик, который ввел прямоугольную систему координат 5. Угол, градусная мера которого больше 900, но меньше 1800 6. Независимая переменная 7. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции 8. Дорога, которую мы выбираем А Л Г О Р И Т М А Б С Ц И С С А Ф У Н К Ц И Я Д Е К А Р Т Т У П О Й А Р Г У М Е Н Т Г Р А Ф И К П Р Я М А Я
Cлайд 5
1. Точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время 2. Одна из координат точки 3. Зависимость одной переменной от другой, при которой каждому значению аргумента соответствует единственное значение зависимой переменной 4. Французский математик, который ввел прямоугольную систему координат 5. Угол, градусная мера которого больше 900, но меньше 1800 6. Независимая переменная 7. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции 8. Дорога, которую мы выбираем А Л Г О Р И Т М А Б С Ц И С С А Ф У Н К Ц И Я Д Е К А Р Т Т У П О Й А Р Г У М Е Н Т Г Р А Ф И К П Р Я М А Я
Cлайд 6
II. Актуализация опорных знаний Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведем пример. Турист проехал на автобусе 15 км от пункта А до пункта В, а затем продолжил движение из пункта В в том же направлении до пункта С , но уже пешком, со скоростью 4 км/ч. На каком расстоянии от пункта А будет турист через 2ч, через 4ч, через 5ч ходьбы? Математической моделью ситуации является выражение y = 15 + 4x, где x – время ходьбы в часах, y – расстояние от А ( в километрах ). С помощью этой модели отвечаем на вопрос задачи: если x = 2, то y =15 + 4 ∙ 2 = 23 если x = 4, то y = 15 + 4 ∙ 4= 31 если x = 6, то y = 15 + 4 ∙ 6 = 39 Математическая модель y = 15 + 4x является линейной функцией. А В С
Cлайд 7
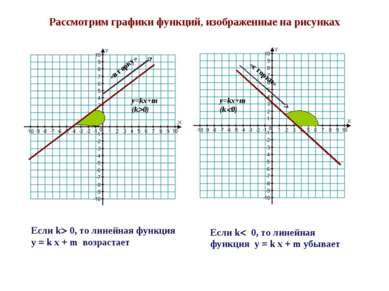
III. Изучение новой темы. Уравнение вида y=k x+ m , где k и m – числа (коэффициенты) называется линейной функцией. Чтобы построить график линейной функции надо , указав конкретное значение x, вычислить соответствующее значение y. Обычно эти результаты оформляют в виде таблицы. Говорят, что x – независимая переменная (или аргумент), y – зависимая переменная. 2 1 1 2 x x x y y x
Cлайд 8
Алгоритм построения графика линейной функции 1) Составить таблицу для линейной функции (каждому значению независимой переменной поставить в соответствие значение зависимой переменной) 2) Построить на координатной плоскости xOy точки 3) Провести через них прямую – график линейной функции Теорема Графиком линейной функции y = k x + m является прямая.
Cлайд 9
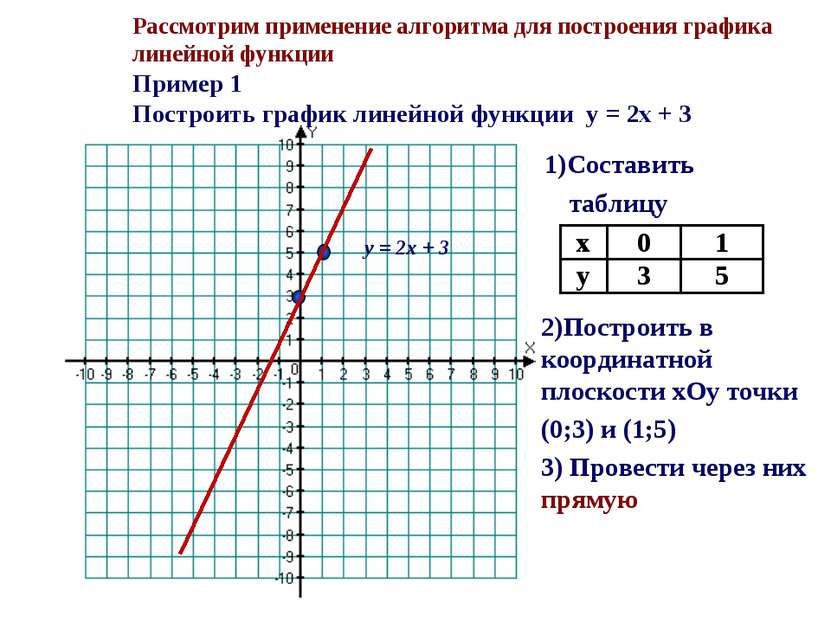
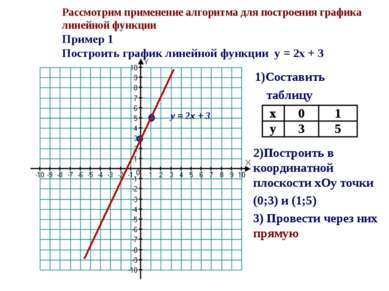Рассмотрим применение алгоритма для построения графика линейной функции Пример 1 Построить график линейной функции y = 2x + 3 1)Составить таблицу 2)Построить в координатной плоскости xОy точки (0;3) и (1;5) 3) Провести через них прямую
Cлайд 10
Если линейную функцию y=k x+ m рассматривать не при всех значениях x, а лишь для значений x из некоторого числового множества X, то пишут : y=k x+ m, где x X ( - знак принадлежности ) Вернёмся к задаче В нашей ситуации независимая переменная может принять любое неотрицательное значение , но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нужно было сделать разумные ограничения на x, скажем, турист идёт не более 6 ч. Теперь запишем более точную математическую модель: y = 15 + 4x, x 0; 6
Cлайд 11
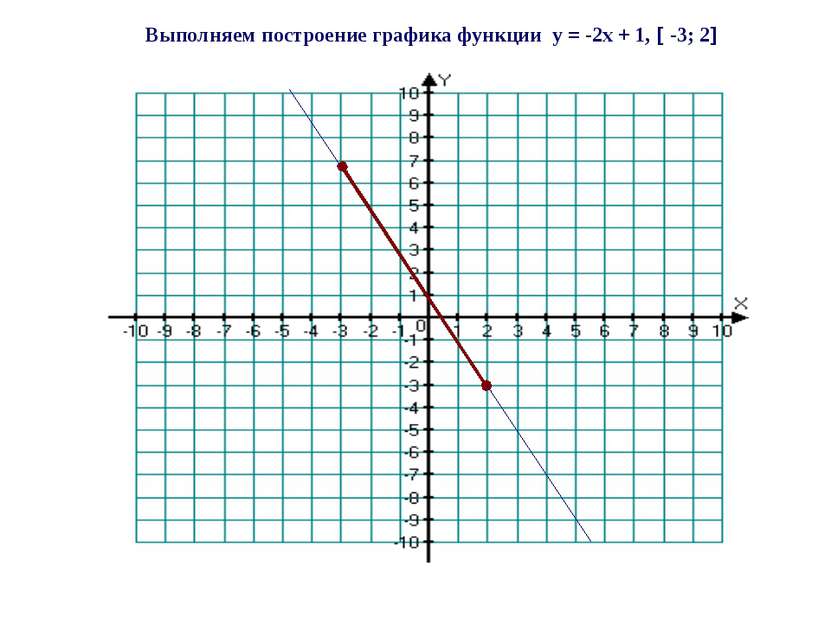
Рассмотрим следующий пример Пример 2 Построить график линейной функции а) y = -2x + 1, -3; 2 ; б) y = -2x + 1, (-3; 2) 1) Составим таблицу для линейной функции y = -2x + 1 2) Построим на координатной плоскости xOy точки (-3;7) и (2;-3) и проведём через них прямую линию. Это график уравнения y = -2x + 1. Далее, выделим отрезок, соединяющий построенные точки. x -3 2 y 7 -3
Cлайд 12
Выполняем построение графика функции y = -2x + 1, -3; 2
Cлайд 13
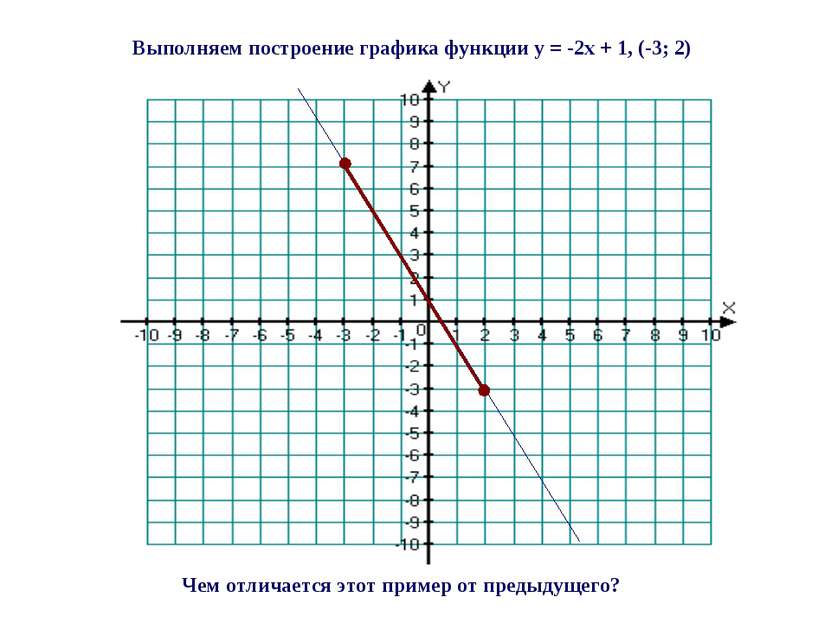
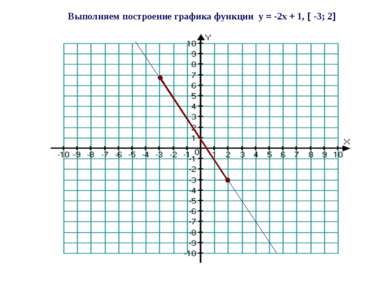
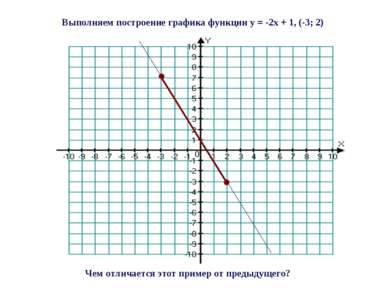Выполняем построение графика функции y = -2x + 1, (-3; 2) Чем отличается этот пример от предыдущего?
Cлайд 14
Рассмотрим графики функций, изображенные на рисунках
Cлайд 15
IV. Закрепление изученной темы Выберите, какая функция является линейной функцией
Cлайд 16
Подумай
Cлайд 17
Молодец
Cлайд 18
Выполните следующее задание Линейная функция задана формулой y = -3x – 5. Найдите её значение при x = 23, x = -5, x = 0
Cлайд 19
Проверка решения Если x = 23, то y = -3 23 – 5=-69 – 5 = -74 Если x = -5, то y = -3 (-5) – 5= 15– 5 = 10 Если x = 0, то y = -3 0– 5= 0 – 5= -5
Cлайд 20
Найдите значение аргумента, при котором линейная функция y = -2x + 2,4 принимает значение равное 20,4? Проверка решения При x = -9 значение функции равно 20,4 20,4 = - 2x + 2,4 2x =2,4 – 20,4 2x = -18 x= -18:2 x = -9
Cлайд 21
Следующее задание Не выполняя построения ответьте на вопрос: графику какой функции принадлежит А (1;0)?
Cлайд 22
Подумай
Cлайд 23
Молодец
Cлайд 24
Запишите координаты точек пересечения графика данной функции с осями координат
Cлайд 25
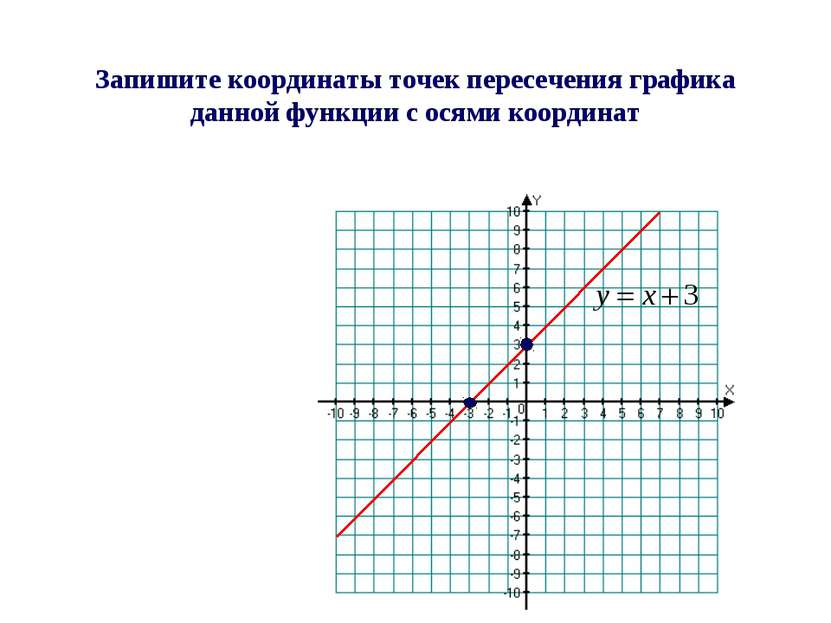
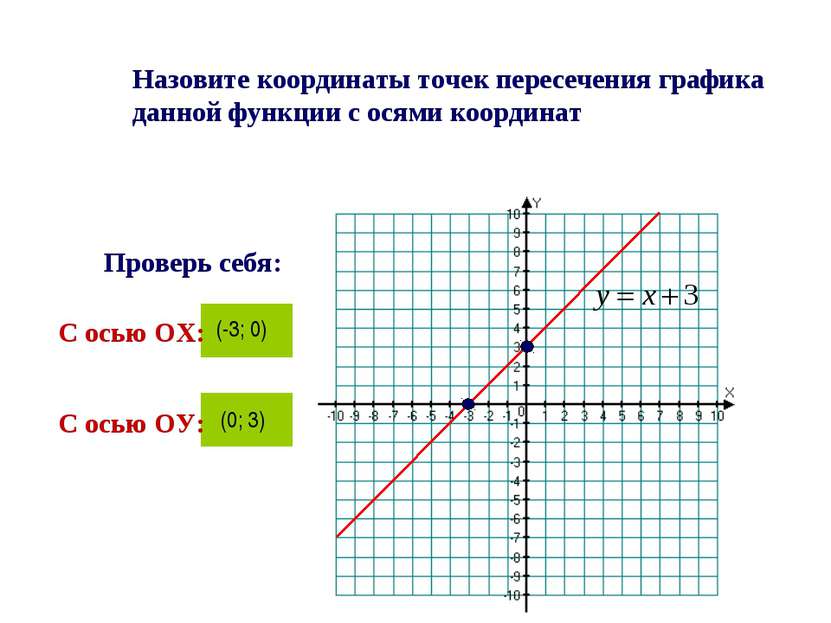
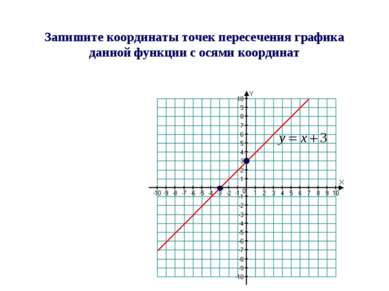
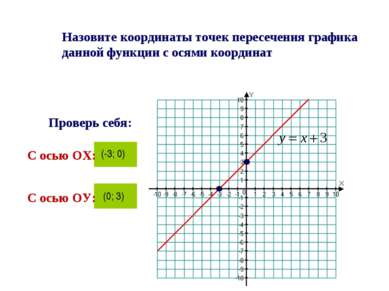Назовите координаты точек пересечения графика данной функции с осями координат С осью ОХ: (-3; 0) Проверь себя: С осью ОУ: (0; 3)
Cлайд 26
Физкультурная минутка для глаз
Cлайд 27
Постройте график линейной функции построение графика.oms
Cлайд 28
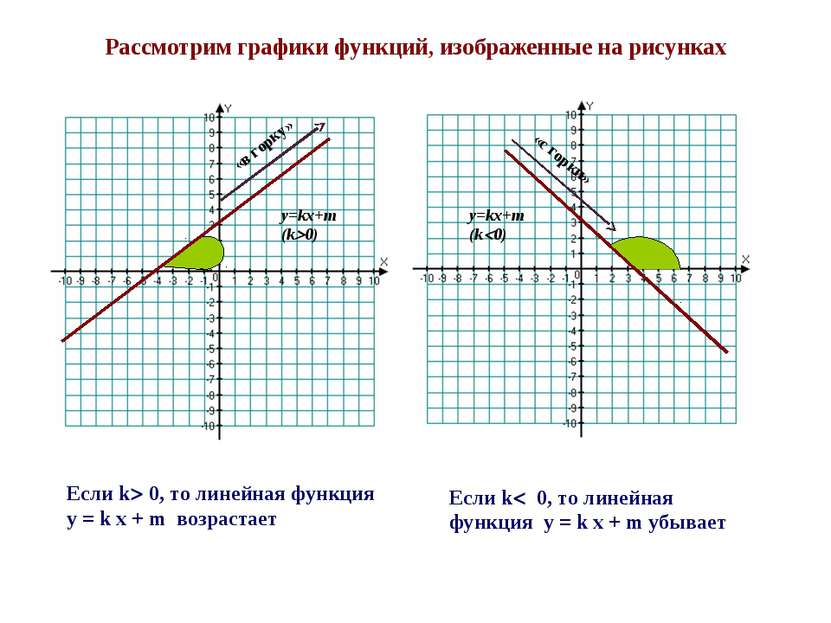
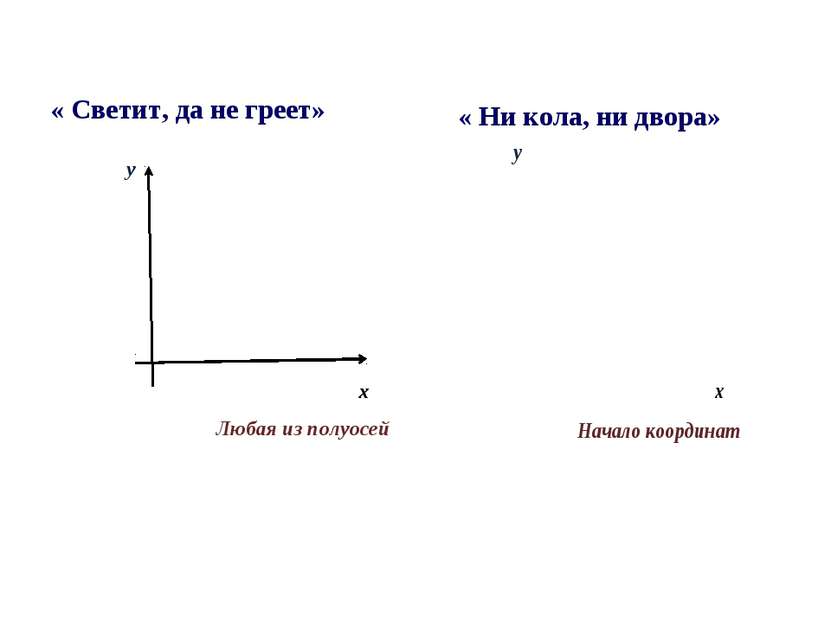
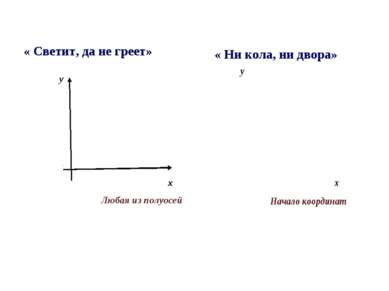
V. Решение занимательных заданий Изобразите пословицы графически «Как аукнется, так и откликнется» «Чем дальше в лес, тем больше дров»
Cлайд 29
« Светит, да не греет» « Ни кола, ни двора»
Cлайд 30
VI. Подведение итогов 1) Какая функция называется линейной ? 2) Что является графиком линейной функции? 3) Сформулировать алгоритм построения графика линейной функции
Cлайд 31
Домашнее задание: «3» - п.8, №8.6, 8.14 (а, б),8.19(а, б) «4», «5» - п.8, №8.51(а, б), 8.52(а, б),8.22 (а)
Cлайд 32
VII. Рефлексия - Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно. - Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно. - У меня не было желания работать. Сегодня не мой день.
Cлайд 33
Используемые источники: «Алгебра (в 2-х частях). Ч. 1: Учебник. 7 класс» А.Г. Мордкович. – М.: Мнемозина, 2010 г. «Алгебра (в 2-х частях). Ч. 2: Задачник. 7 класс» А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина, Е.Е. Тульчинская. – М.: Мнемозина, 2010 г. «Математика, 5-11 классы. Уроки учительского мастерства» Е.В. Алтухова, Т.Н. Видеман и др. – В.: Учитель, 2009 г. http://fcior.edu.ru/
