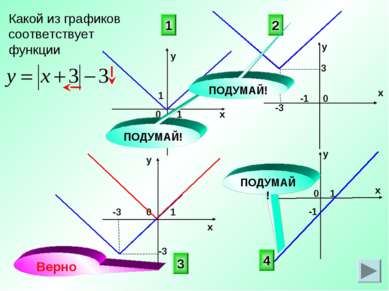
X
Код презентации скопируйте его
Графики функций
Скачать эту презентацию
Презентация на тему Графики функций
Скачать эту презентациюCлайд 1
Cлайд 2
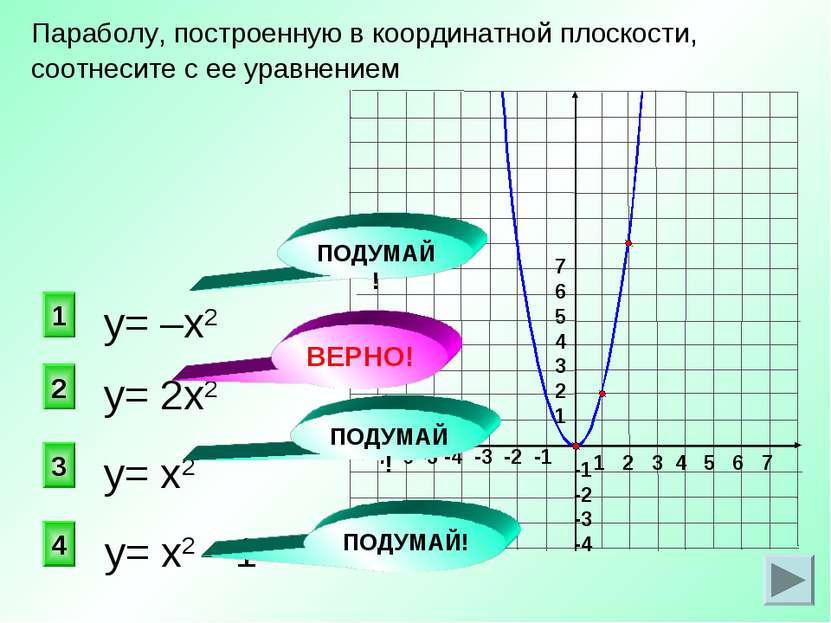
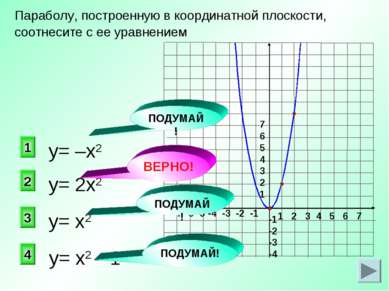у= 2х2 2 1 3 4 Параболу, построенную в координатной плоскости, соотнесите с ее уравнением у= –х2 у= х2 у= х2 – 1 ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 3
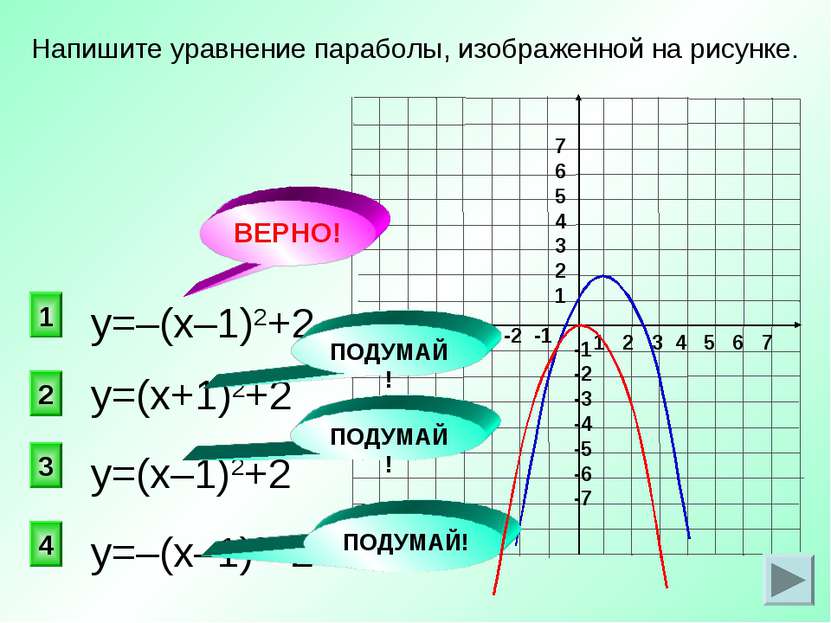
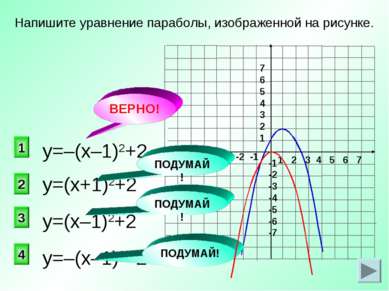1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 у=(х+1)2+2 1 2 3 4 ВЕРНО! Напишите уравнение параболы, изображенной на рисунке. у=–(х–1)2+2 у=(х–1)2+2 у=–(х–1)2–2 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 4
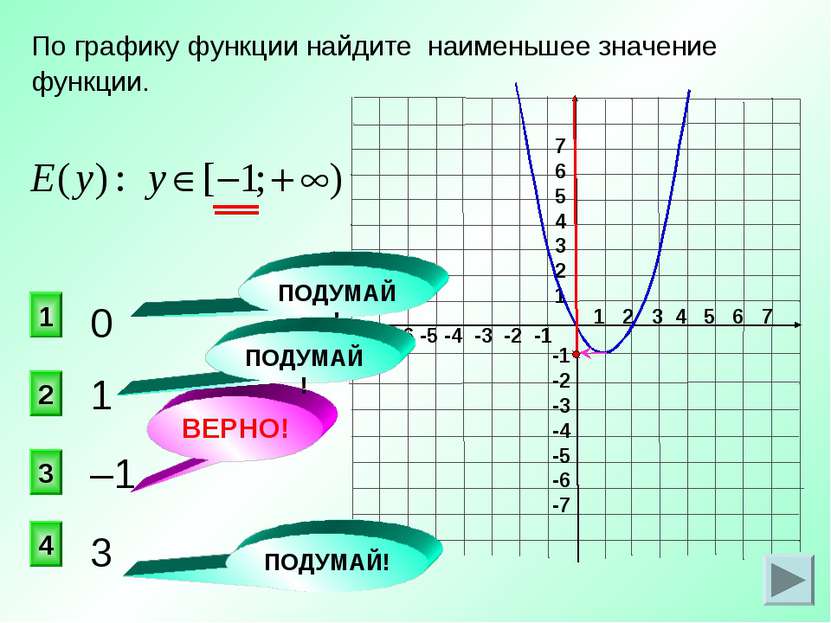
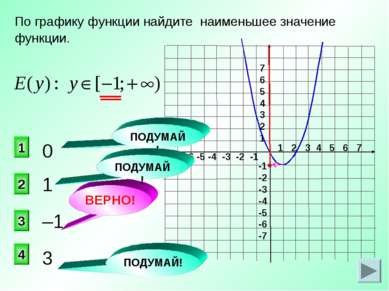1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 1 3 2 1 4 ВЕРНО! По графику функции найдите наименьшее значение функции. 0 –1 3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 5
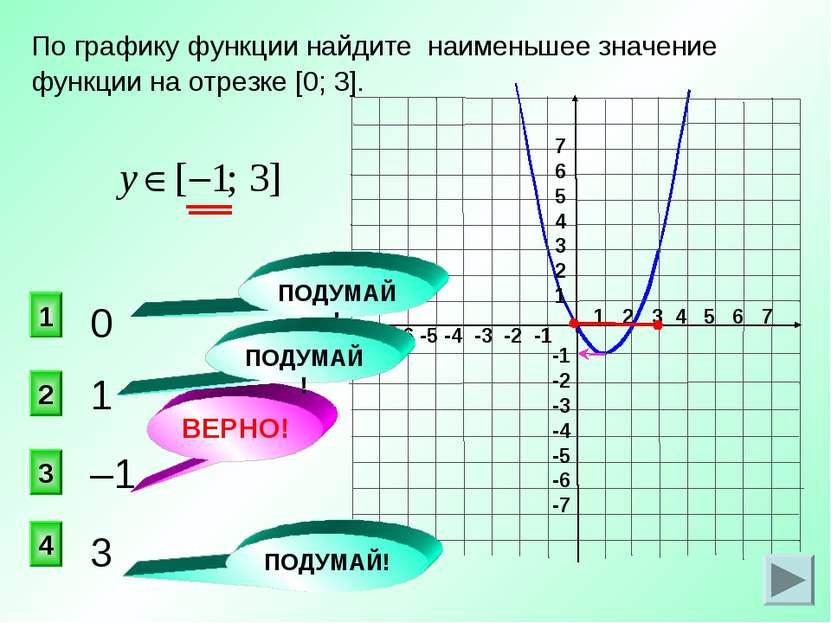
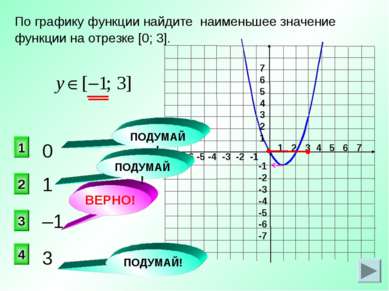1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 1 3 2 1 4 ВЕРНО! По графику функции найдите наименьшее значение функции на отрезке [0; 3]. 0 –1 3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 6
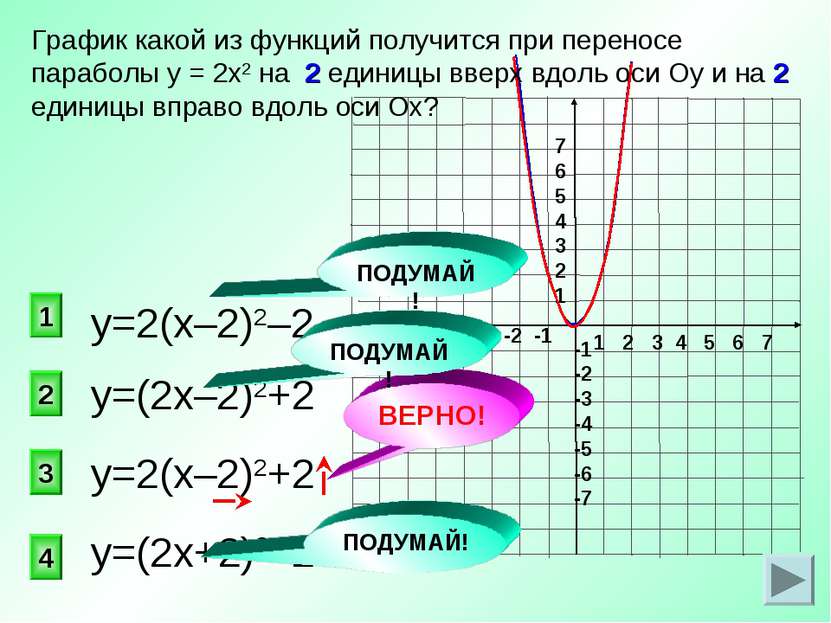
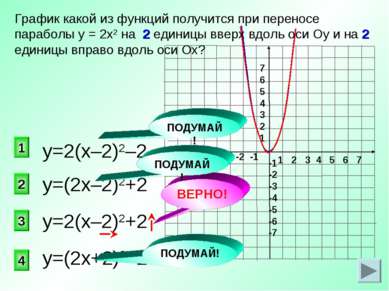у=(2х–2)2+2 3 2 1 4 График какой из функций получится при переносе параболы у = 2х2 на 2 единицы вверх вдоль оси Оу и на 2 единицы вправо вдоль оси Ох? у=2(х–2)2–2 у=2(х–2)2+2 у=(2х+2)2–2 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 7
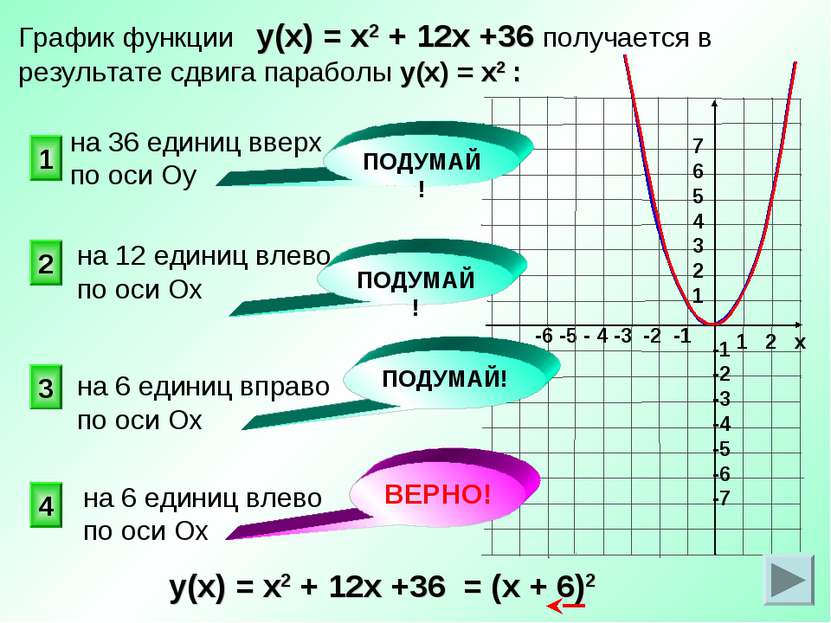
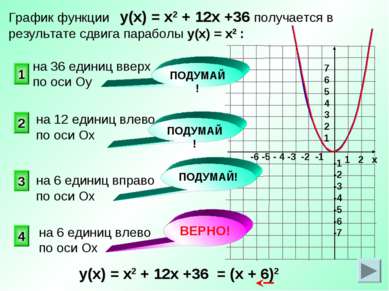ВЕРНО! 4 2 1 3 График функции у(х) = х2 + 12х +36 получается в результате сдвига параболы у(х) = х2 : на 12 единиц влево по оси Ох ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! на 36 единиц вверх по оси Оу на 6 единиц вправо по оси Ох на 6 единиц влево по оси Ох у(х) = х2 + 12х +36 = (х + 6)2
Cлайд 8
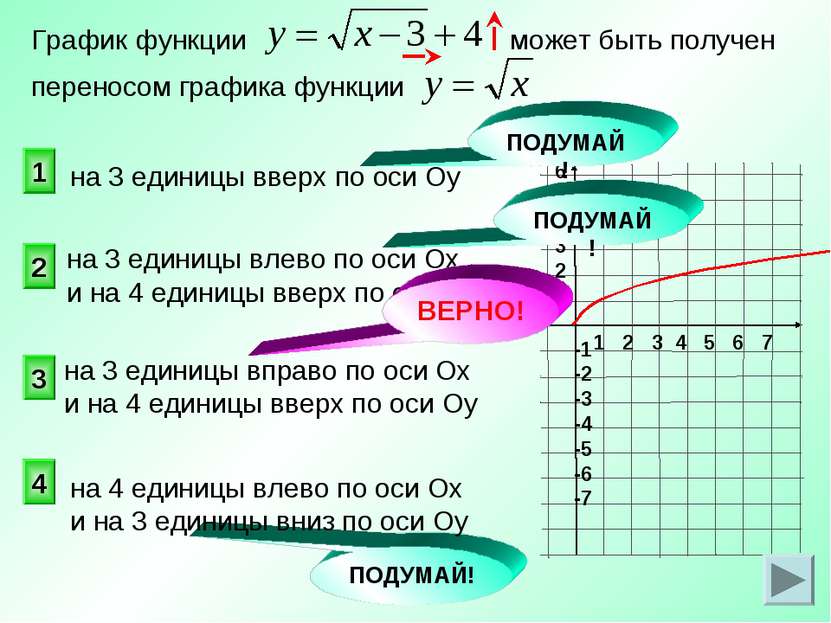
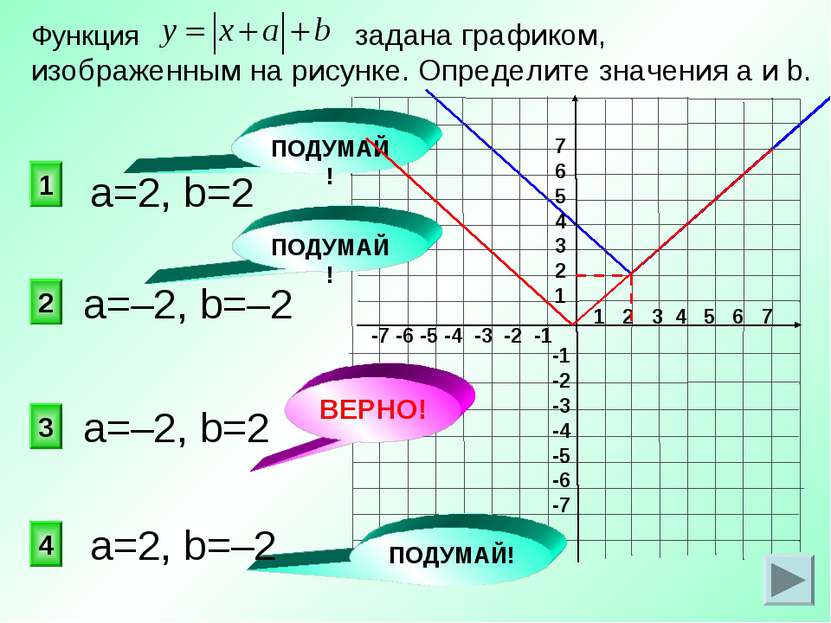
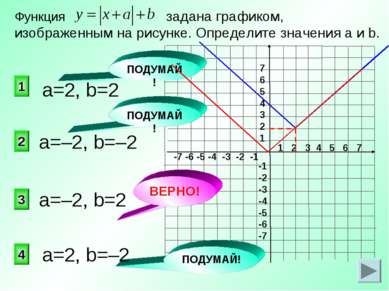
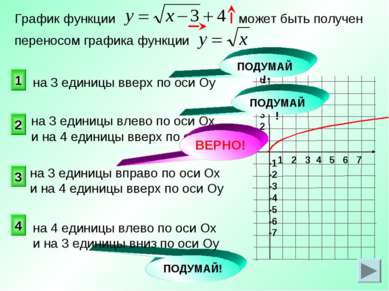на 3 единицы влево по оси Ох и на 4 единицы вверх по оси Оу График функции может быть получен переносом графика функции 3 2 1 4 на 3 единицы вверх по оси Оу ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! на 3 единицы вправо по оси Ох и на 4 единицы вверх по оси Оу на 4 единицы влево по оси Ох и на 3 единицы вниз по оси Оу ВЕРНО!
Cлайд 9
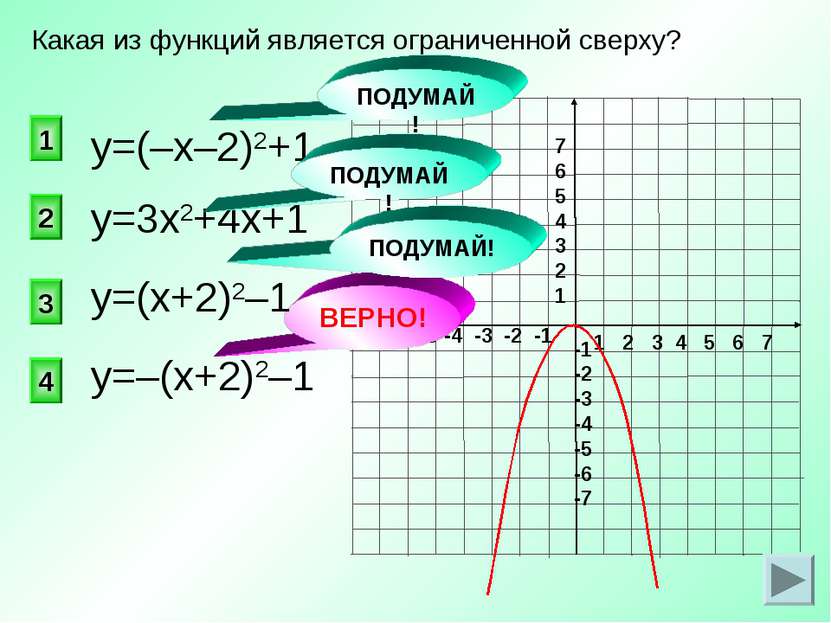
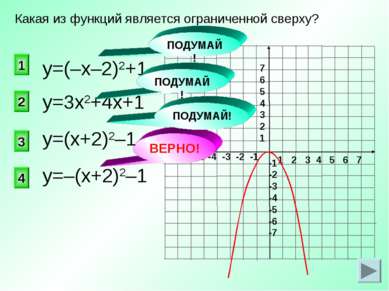ВЕРНО! у=3х2+4х+1 4 2 1 3 Какая из функций является ограниченной сверху? у=(–х–2)2+1 у=(х+2)2–1 у=–(х+2)2–1 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 10
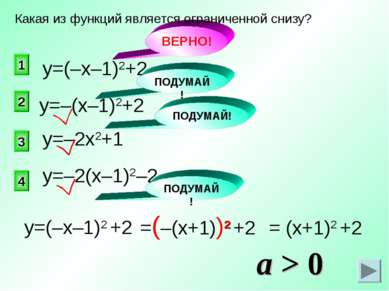ВЕРНО! 1 2 4 3 Какая из функций является ограниченной снизу? у=(–х–1)2+2 у=–2х2+1 у=–2(х–1)2–2 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! у=–(х–1)2+2 у=(–х–1)2 +2 =(–(х+1))2 +2 = (х+1)2 +2 a > 0
Cлайд 11
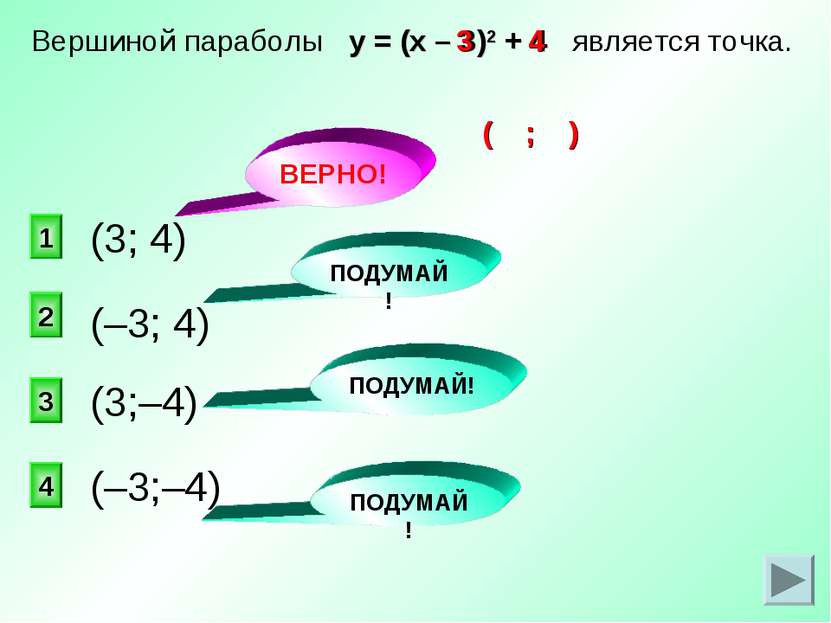
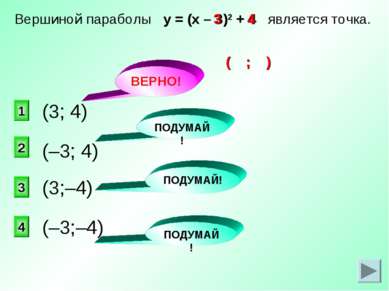ВЕРНО! 1 2 4 3 Вершиной параболы у = (х – 3)2 + 4 является точка. (3; 4) ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! (–3; 4) (3;–4) (–3;–4) 4 3 ( ; )
Cлайд 12
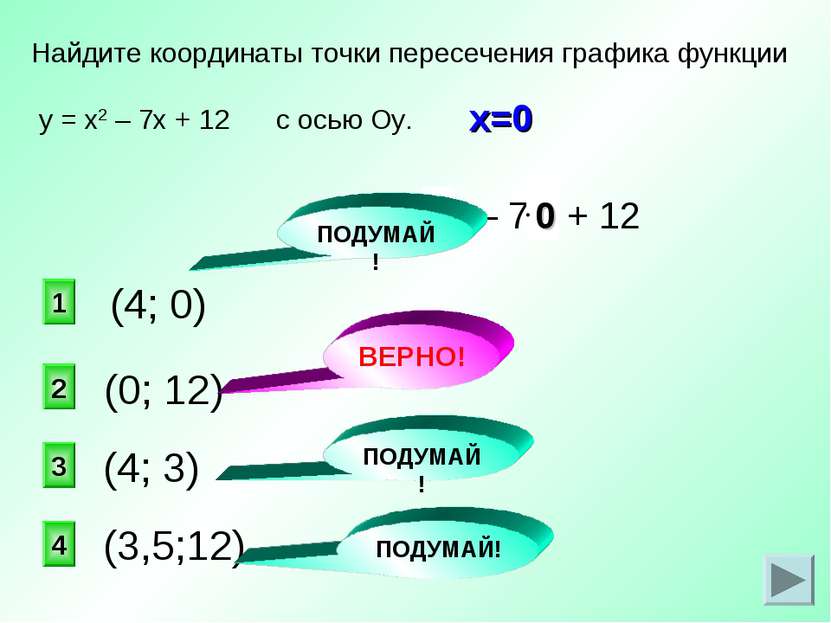
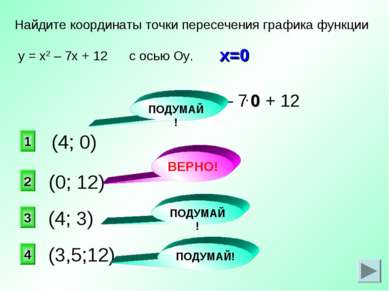у = х2 – 7х + 12 (0; 12) Найдите координаты точки пересечения графика функции у = х2 – 7х + 12 с осью Оу. 0 2 1 3 4 (4; 0) (4; 3) (3,5;12) ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! х=0
Cлайд 13
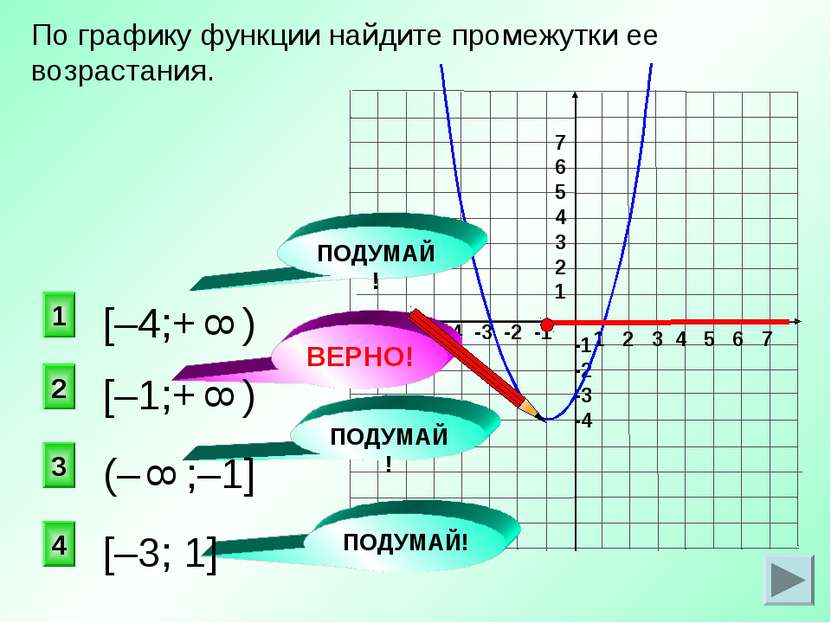
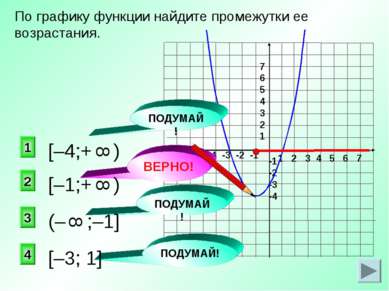1 3 4 По графику функции найдите промежутки ее возрастания. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! 2 (– ;–1] 8 [–3; 1]
Cлайд 14
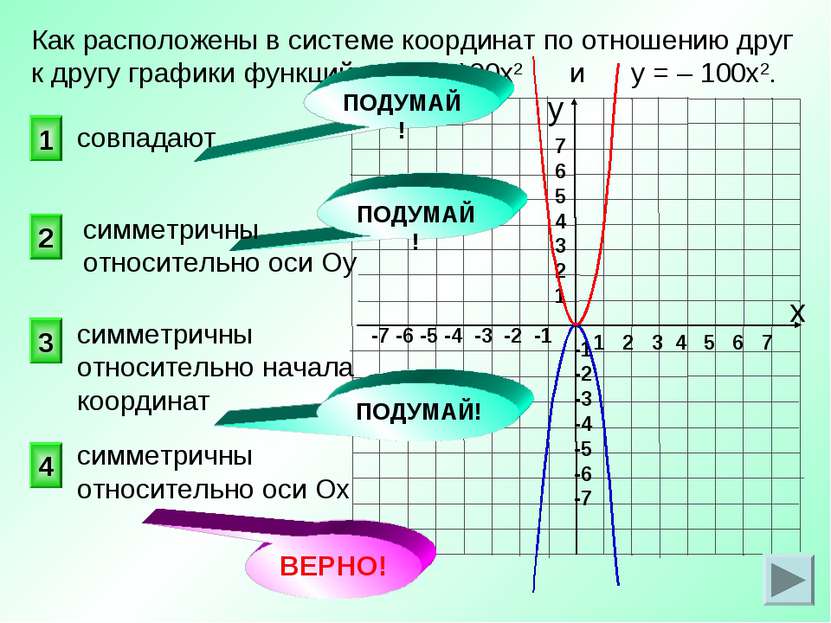
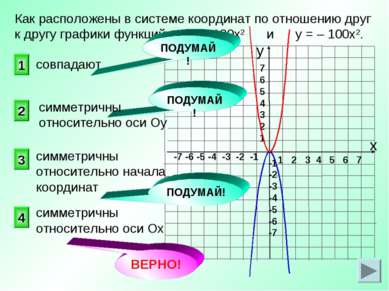ВЕРНО! 4 2 1 3 Как расположены в системе координат по отношению друг к другу графики функций у = 100х2 и у = – 100х2. совпадают ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! симметричны относительно оси Ох симметричны относительно оси Оу симметричны относительно начала координат
Cлайд 15
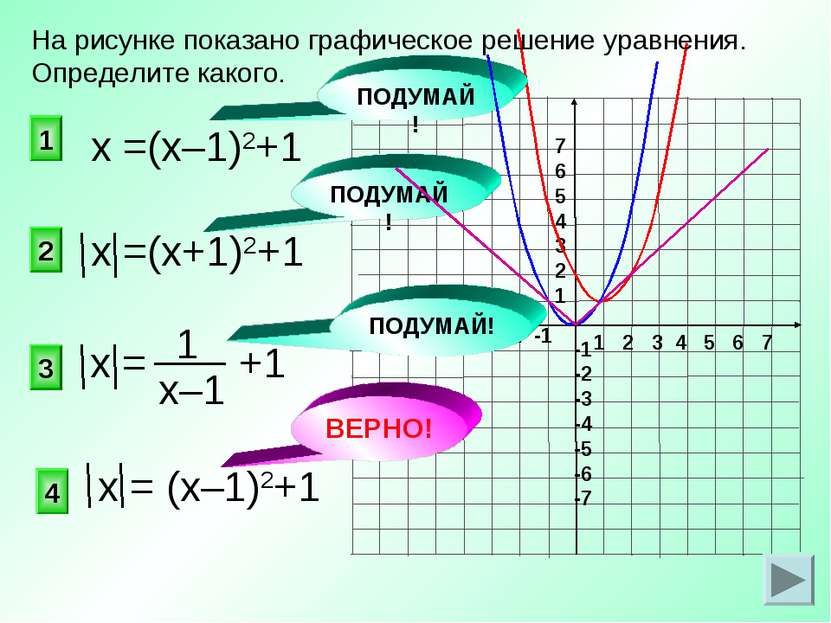
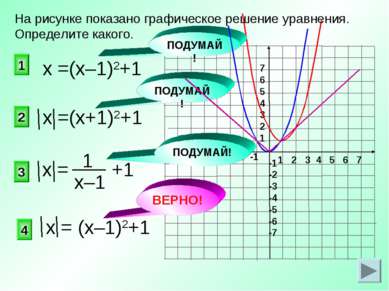1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 ВЕРНО! х =(х+1)2+1 4 2 1 3 На рисунке показано графическое решение уравнения. Определите какого. х =(х–1)2+1 х = +1 х = (х–1)2+1 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 16
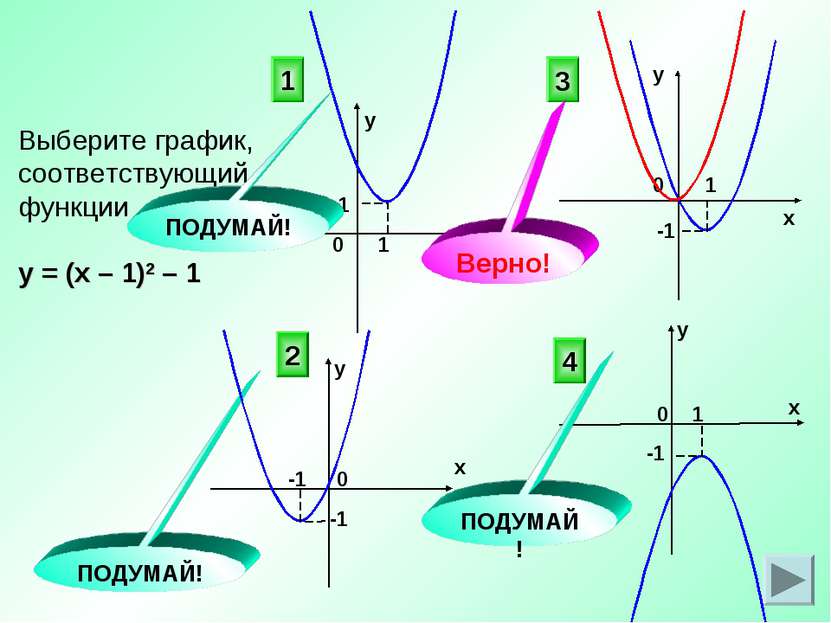
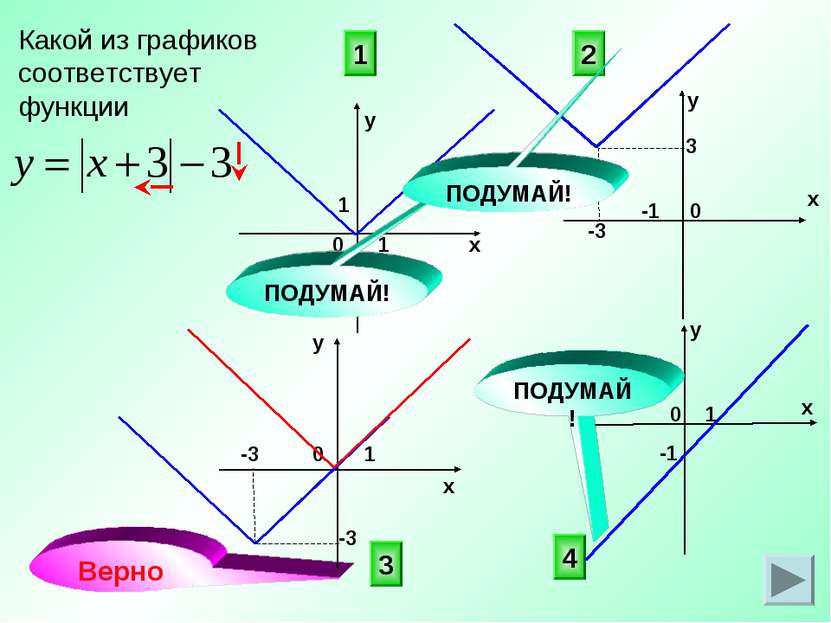
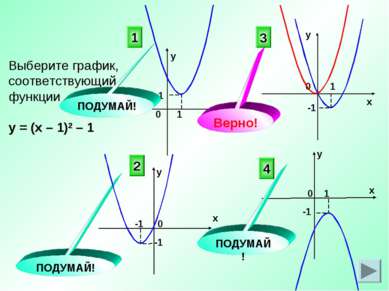Выберите график, соответствующий функции у = (х – 1)2 – 1 3 4 2 ПОДУМАЙ! ПОДУМАЙ! 0 0 х у у х х х у у 0 0 1 -1 1 1 -1 -1 -1 1 1 Верно! ПОДУМАЙ!
Cлайд 17
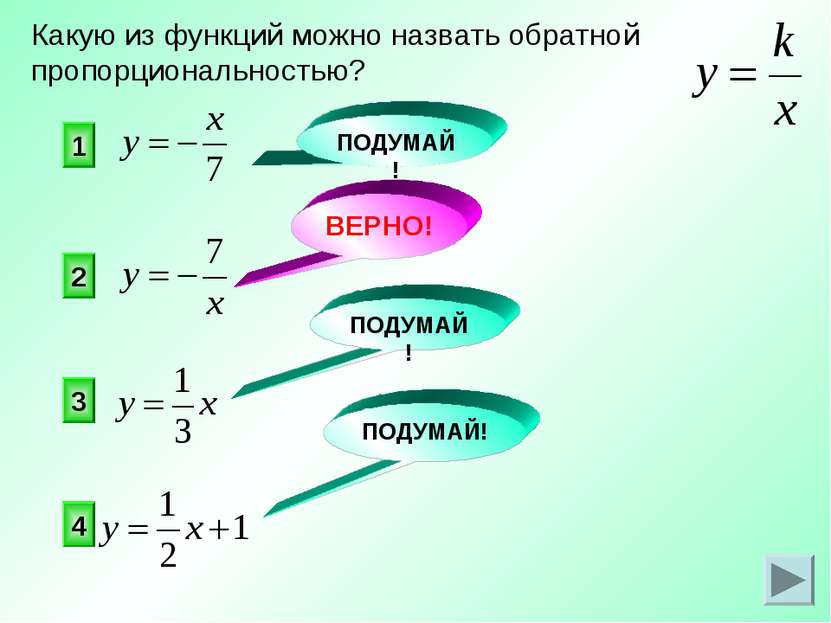
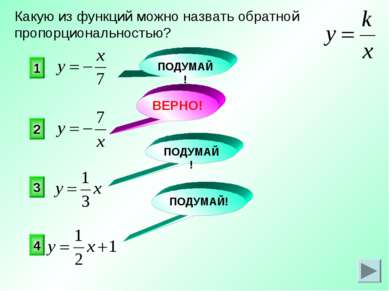1 3 4 Какую из функций можно назвать обратной пропорциональностью? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! 2
Cлайд 18
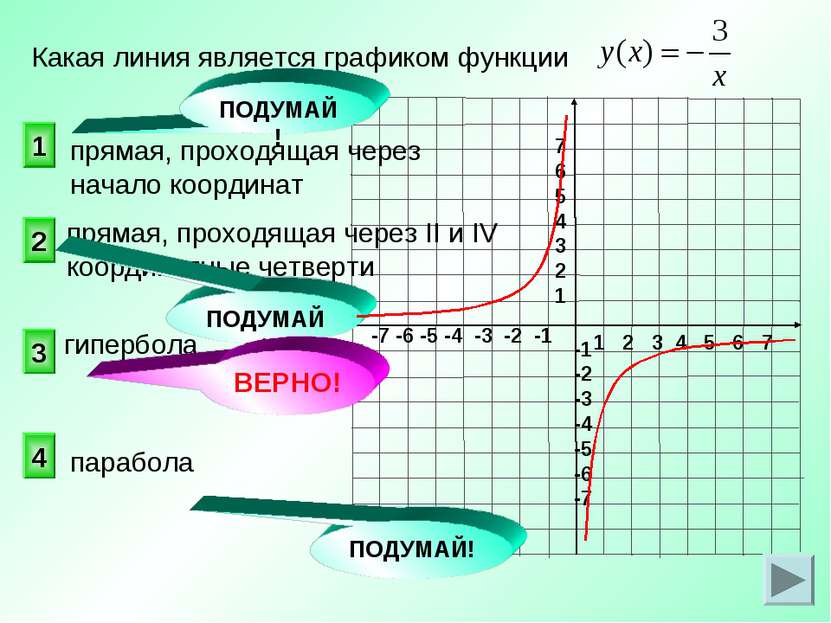
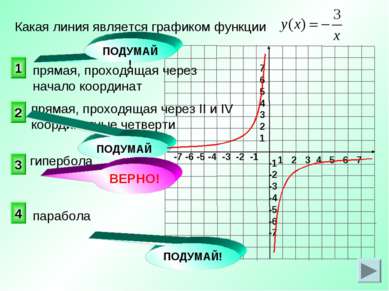прямая, проходящая через II и IV координатные четверти Какая линия является графиком функции 3 2 1 4 прямая, проходящая через начало координат ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! гипербола парабола ВЕРНО!
Cлайд 19
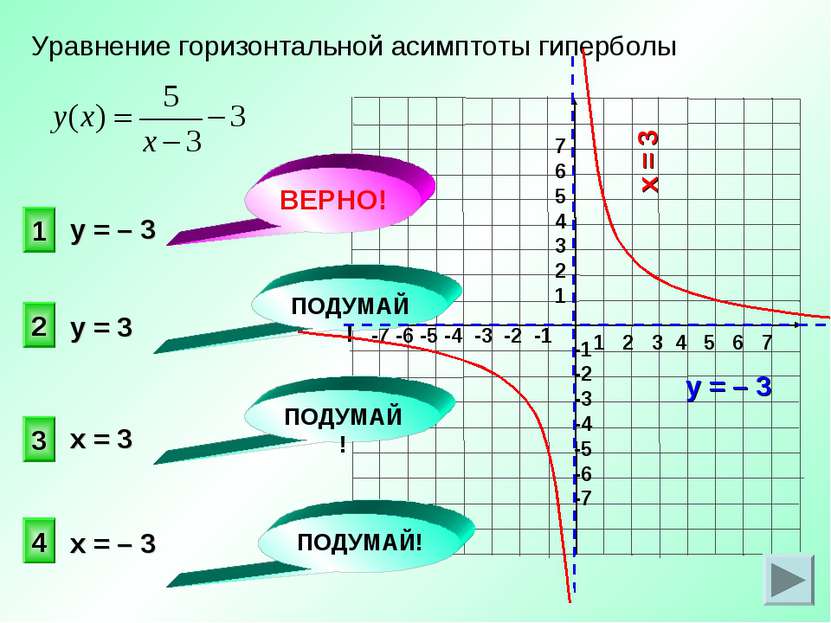
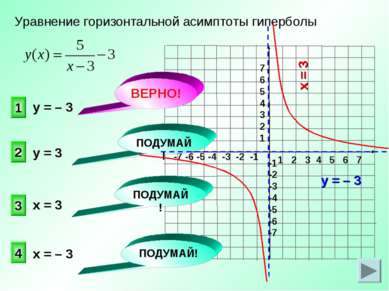Уравнение горизонтальной асимптоты гиперболы 1 2 3 4 у = – 3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! ВЕРНО! у = – 3 у = 3 х = 3 х = – 3 х = 3
Cлайд 20
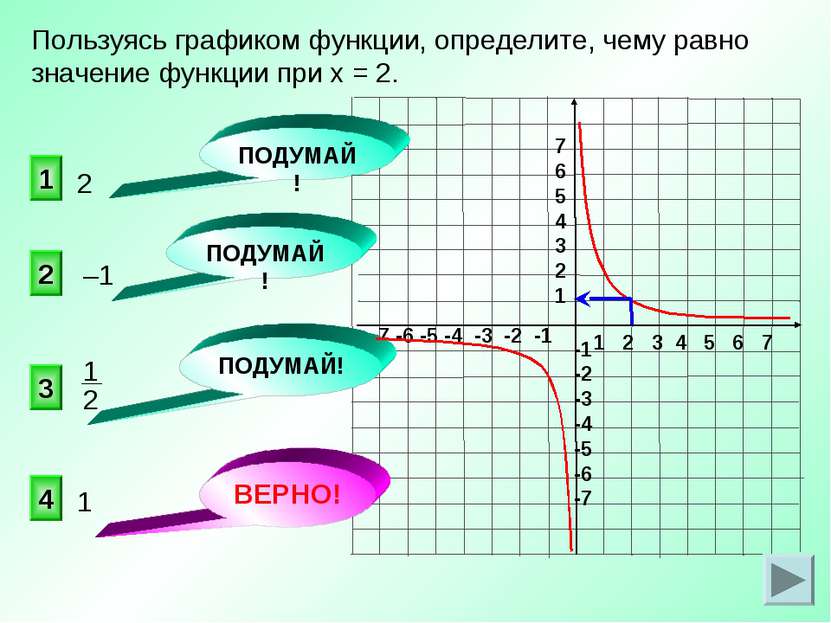
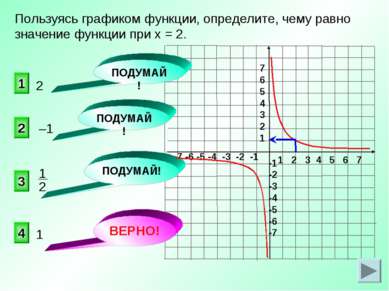Пользуясь графиком функции, определите, чему равно значение функции при х = 2. 4 2 1 3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! ВЕРНО! –1 2 1
Cлайд 21
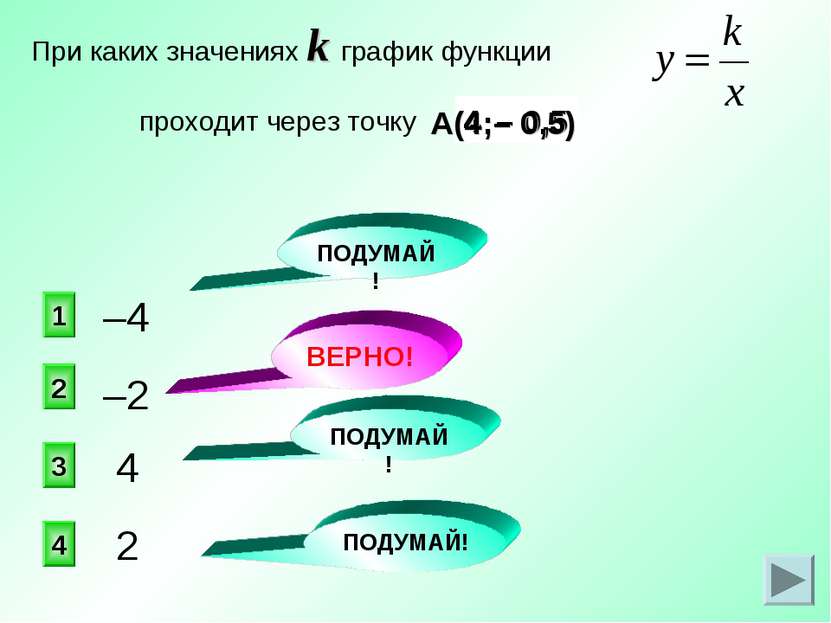
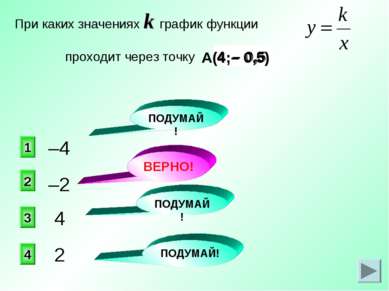– 0,5 4 А(4;– 0,5) –2 2 1 3 4 При каких значениях k график функции проходит через точку –4 4 2 ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 22
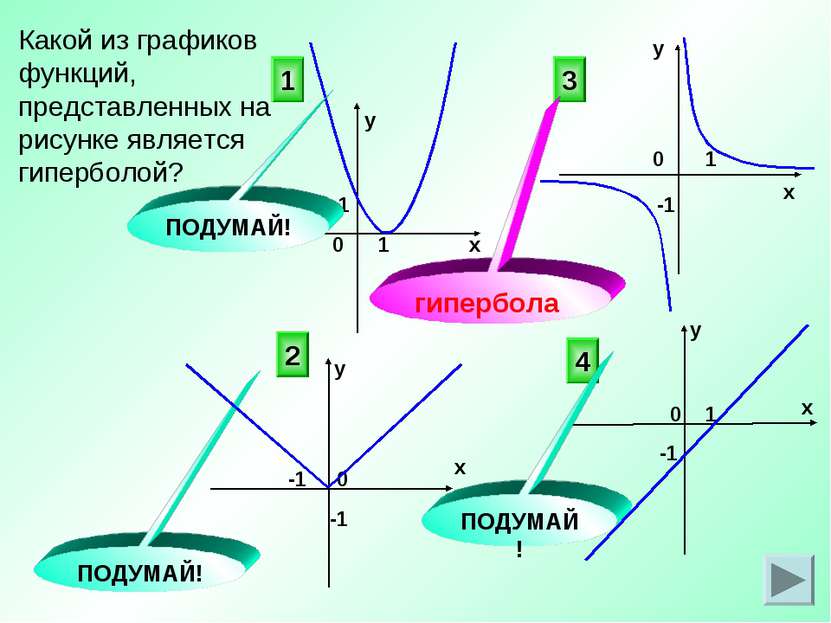
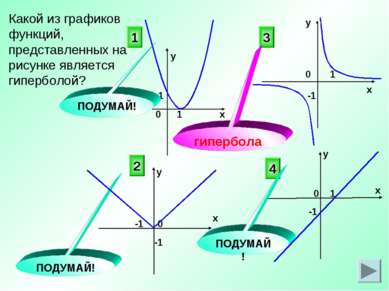Какой из графиков функций, представленных на рисунке является гиперболой? 3 4 2 ПОДУМАЙ! ПОДУМАЙ! 0 0 х у у х х х у у 0 0 1 -1 1 1 -1 -1 -1 1 1 гипербола ПОДУМАЙ!
Cлайд 23
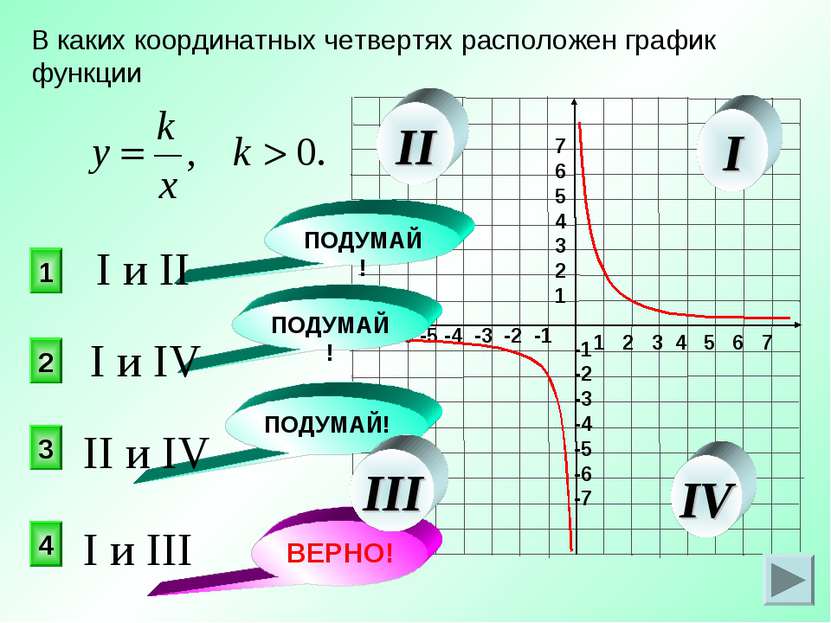
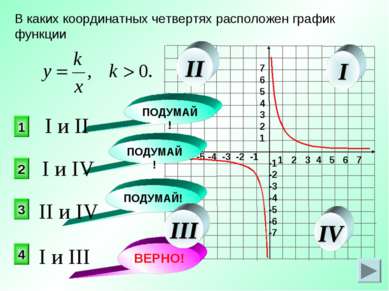В каких координатных четвертях расположен график функции 4 2 1 3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! ВЕРНО! I и III II и IV I и IV I и II
Cлайд 24
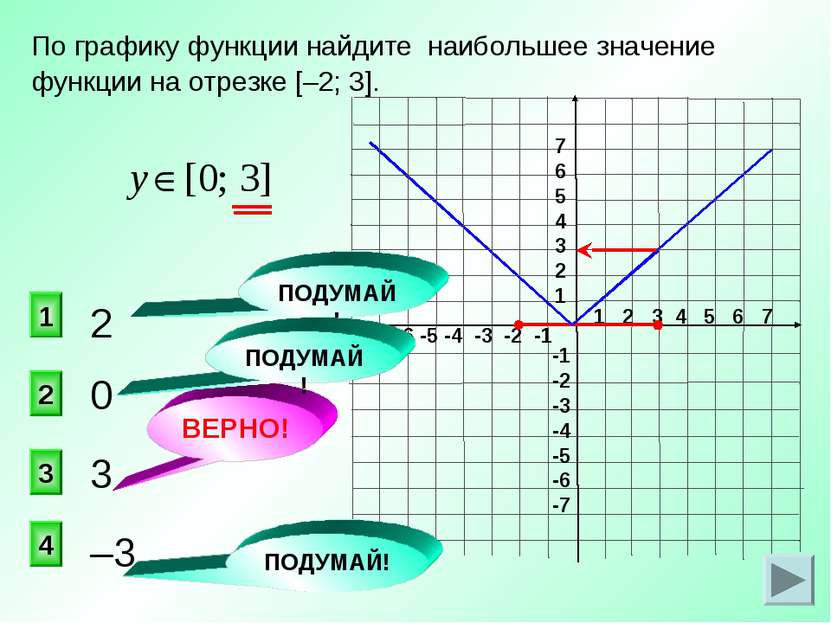
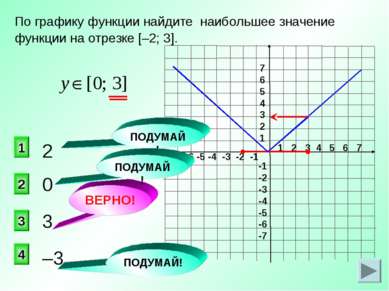1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 0 3 2 1 4 ВЕРНО! По графику функции найдите наибольшее значение функции на отрезке [–2; 3]. 2 3 –3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 25
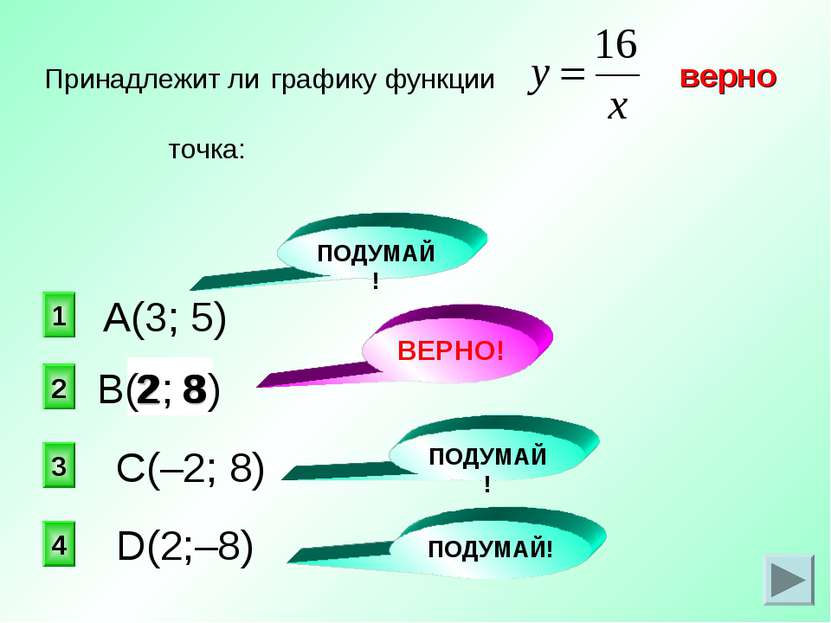
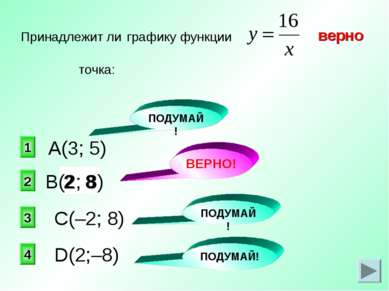8 2 верно 2 1 3 4 Принадлежит ли графику функции точка: А(3; 5) С(–2; 8) D(2;–8) ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! В(2; 8)
Cлайд 26
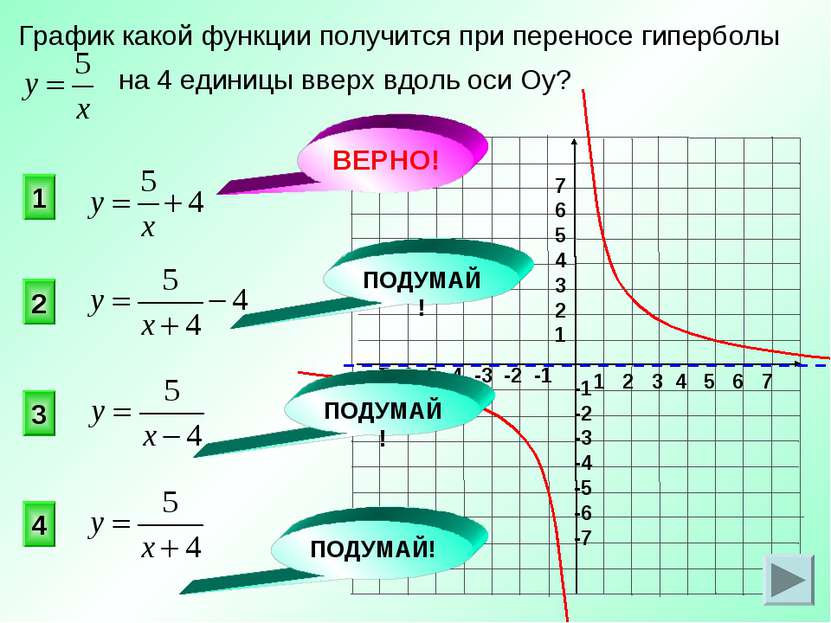
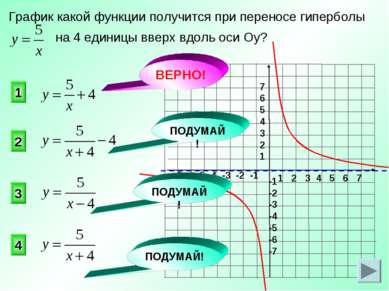График какой функции получится при переносе гиперболы на 4 единицы вверх вдоль оси Оу? 1 2 3 4 ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
Cлайд 27
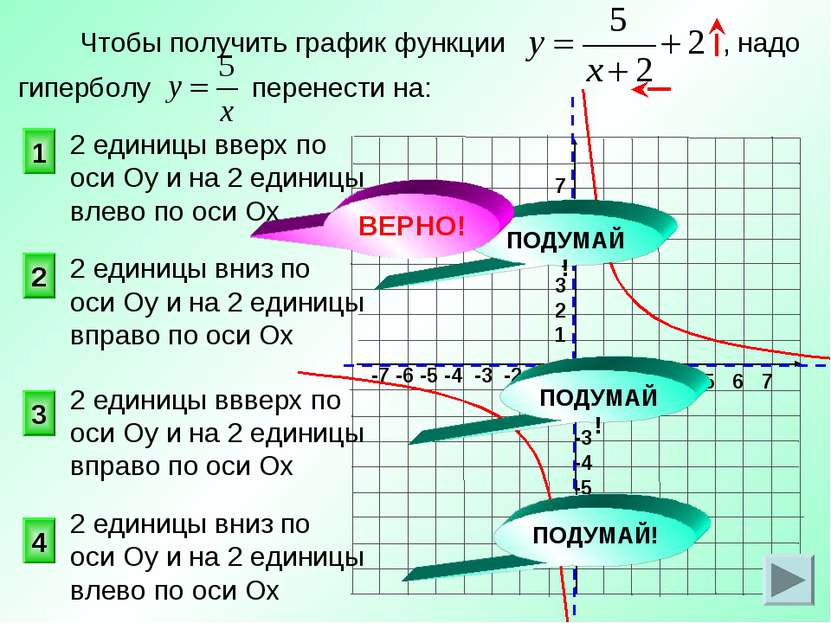
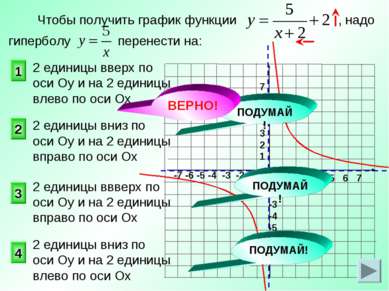Чтобы получить график функции , надо гиперболу перенести на: 1 2 3 4 2 единицы вверх по оси Оу и на 2 единицы влево по оси Ох 2 единицы вниз по оси Оу и на 2 единицы вправо по оси Ох 2 единицы вниз по оси Оу и на 2 единицы влево по оси Ох 2 единицы ввверх по оси Оу и на 2 единицы вправо по оси Ох ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! ВЕРНО!
Cлайд 28
1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 3 2 1 4 ВЕРНО! a=2, b=2 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ! a=2, b=–2 a=–2, b=2 a=–2, b=–2
Cлайд 29
Какой из графиков соответствует функции 3 4 2 0 х у х у 0 1 1 -1 1 1 Верно 0 у х 1 -3 -3 ПОДУМАЙ! ПОДУМАЙ! ПОДУМАЙ!
