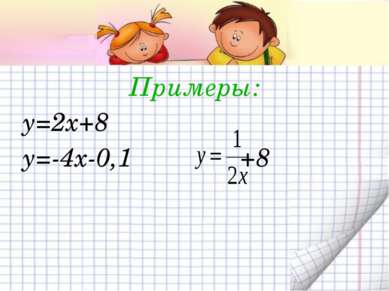X
Код презентации скопируйте его
Линейная функция и её график
Скачать эту презентацию
Презентация на тему Линейная функция и её график
Скачать эту презентациюCлайд 1
Линейная функция и её график АВТОР ЮРАКОВА Н.Г. УЧИТЕЛЬ МАТЕМАТИКИ
Cлайд 2
Функция вида y = kx +b, где k и b числа, а x и y переменные, называется линейной функцией. x – независимая переменная (аргумент) y – зависимая переменная (функция)
Cлайд 3
Примеры: y=2x+8 y=-4x-0,1 +8
Cлайд 4
Выбрав значение х (аргумента), можно легко вычислить значение y (функции) у = 2 х + 3 х =0 у=0+3=3 х =2 у=4+3=7
Cлайд 5
Задание: построить графики функций у= 0,5х и у=0,5х+2 у=0,5х у=0,5х+2 0
Cлайд 6
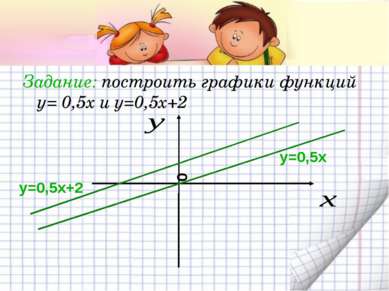
Вывод: график функции y=kx+b, где k не равное нулю число, есть прямая, параллельная прямой y=kx. Графиком линейной функции является прямая. Для построения прямой достаточно координат двух точек.
Cлайд 7
№ 317 ( в тетрадях, с комментированием, оформление в виде таблице)
Cлайд 8
Число k называется угловым коэффициентом прямой – графика функции у = kx + b. Если k>0, то угол наклона прямой у=kx+b к оси х острый; если k
Cлайд 9
Свойства взаимного расположения прямых у1=k1x+b1 у2=k2x+b2
Cлайд 10
а) Если k1≠k2,то прямые пересекаются; б) Если k1=k2 и b1≠b2 ,то прямые параллельны; в) Если k1=k2 и b1=b2 ,то прямые совпадают.
Cлайд 11
№ 319 (а,г,д) у=1/2х-3 У=х+1,5 у=-2х+1
Cлайд 12
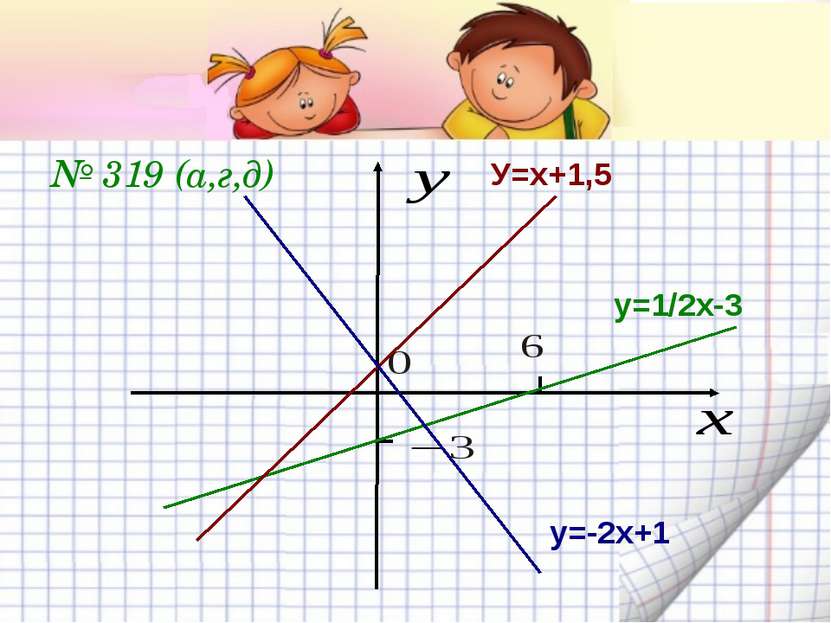
№ 318 у = –3х + 1,5 а) х = –1,5; у = – 3 ∙ (– 1,5) + 1,5 = 6 х = 2,5; у = –3 ∙ 2,5 + 1,5 = –7,5 + 1,5 = –6 х = 4; у = –3 ∙ 4 + 1,5 = –2 + 1,5 = –10,5
Cлайд 13
б) у = – 4,5; –3х + 1,5 = –4,5 –3х = –4,5 – 1,5 –3х = –6 х = 2 у = 0; –3х + 1,5 = 0 –3х = –1,5 х = 0,5 у = 0; –3х + 1,5 = 1,5 –3х = 0 х = 0
Cлайд 14
Домашнее задание: п. 16, № 318, № 320, № 332.
