X
Код презентации скопируйте его
Определенный интеграл
Скачать эту презентациюПрезентация на тему Определенный интеграл
Скачать эту презентациюCлайд 2
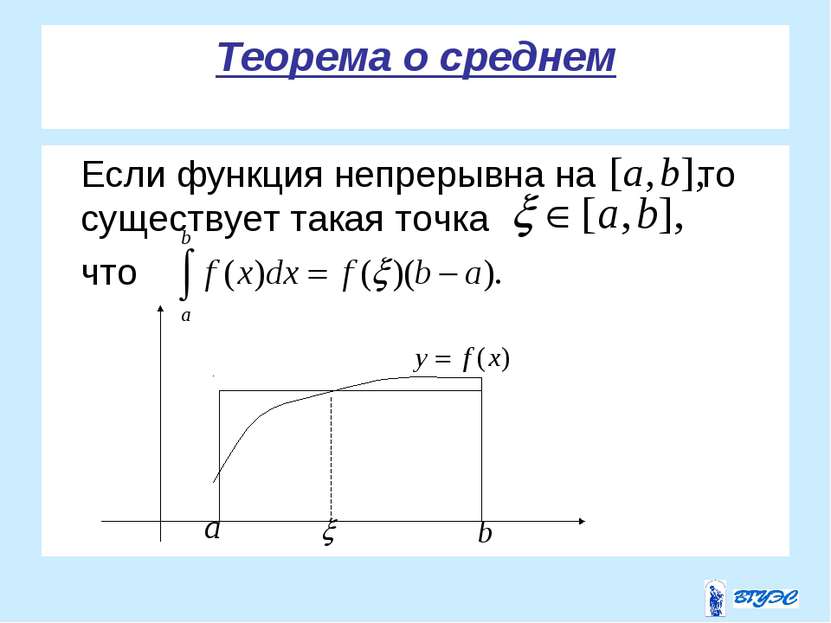
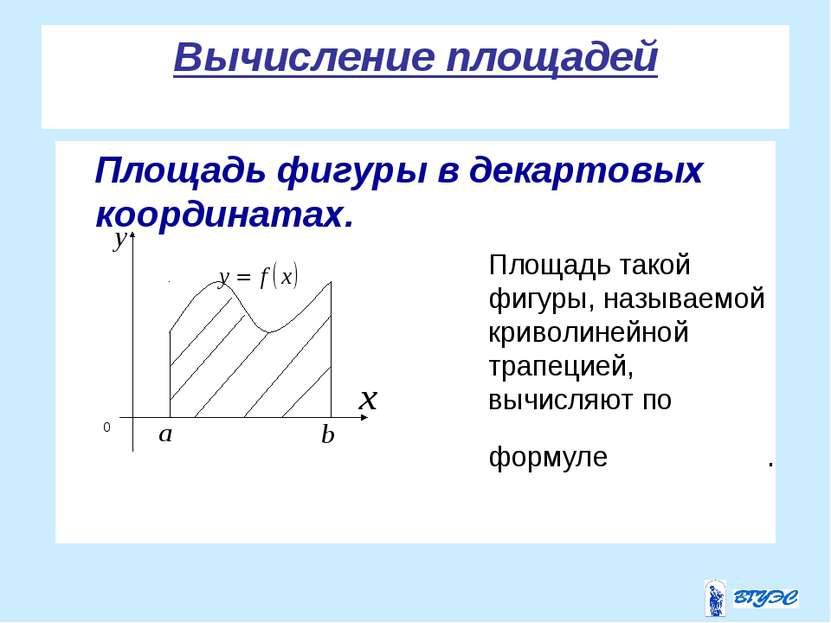
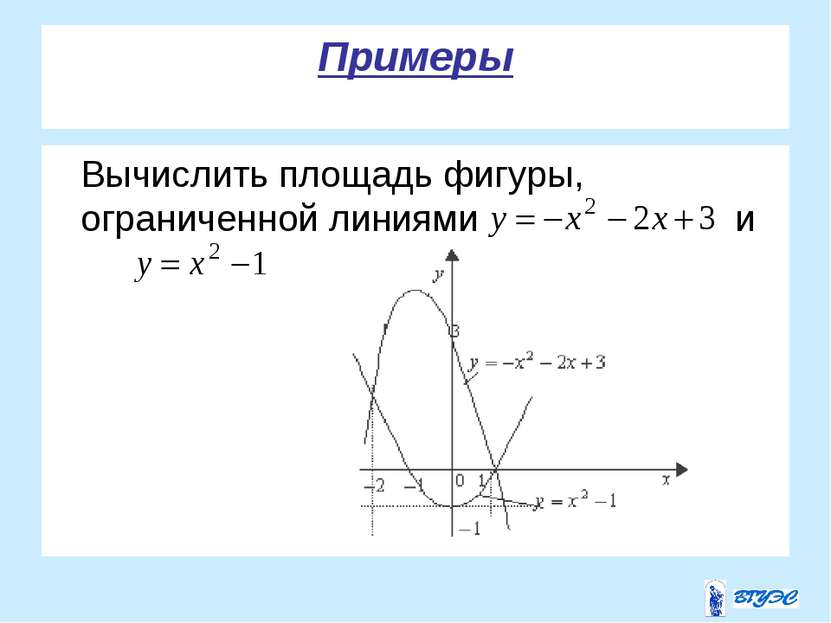
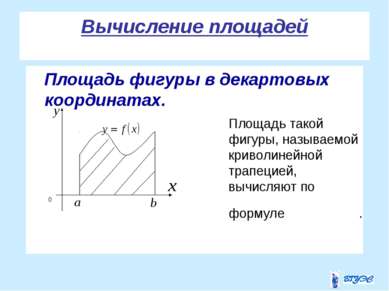
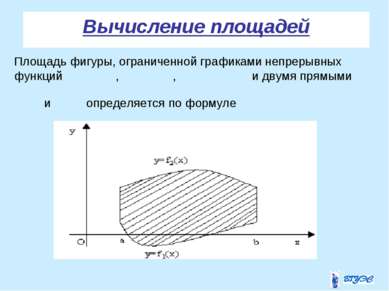
 Задача о вычислении площади плоской фигуры Решим задачу о вычислении площади фигуры, ограниченной графиком функции , отрезками прямых , и осью Ox.Такую фигуру называют криволинейной трапецией a b
Задача о вычислении площади плоской фигуры Решим задачу о вычислении площади фигуры, ограниченной графиком функции , отрезками прямых , и осью Ox.Такую фигуру называют криволинейной трапецией a b
Cлайд 19
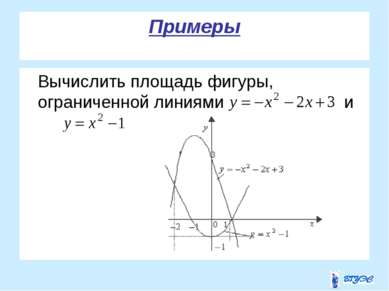
 Пример . Вычислить несобственный интеграл (или установить его расходимость) . Этот несобственный интеграл расходится.
Пример . Вычислить несобственный интеграл (или установить его расходимость) . Этот несобственный интеграл расходится.
Cлайд 24
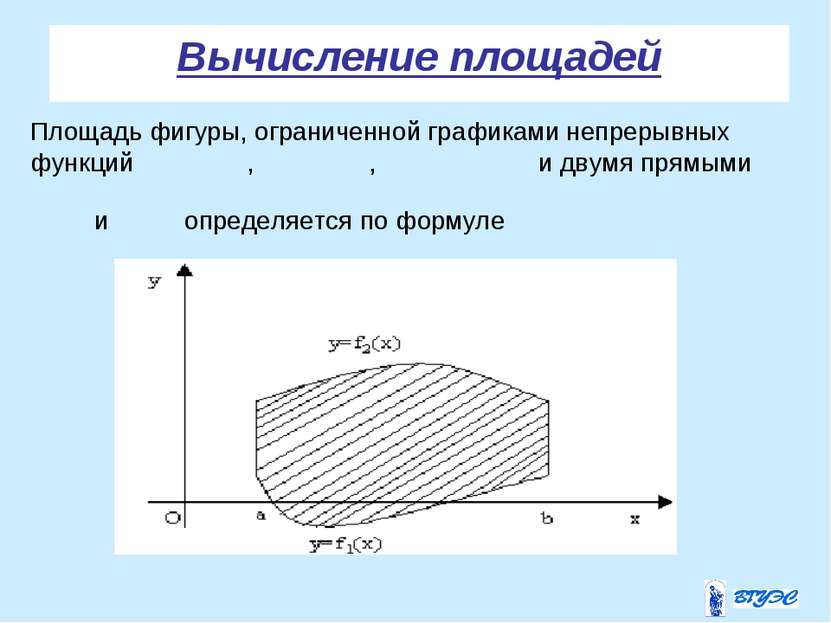
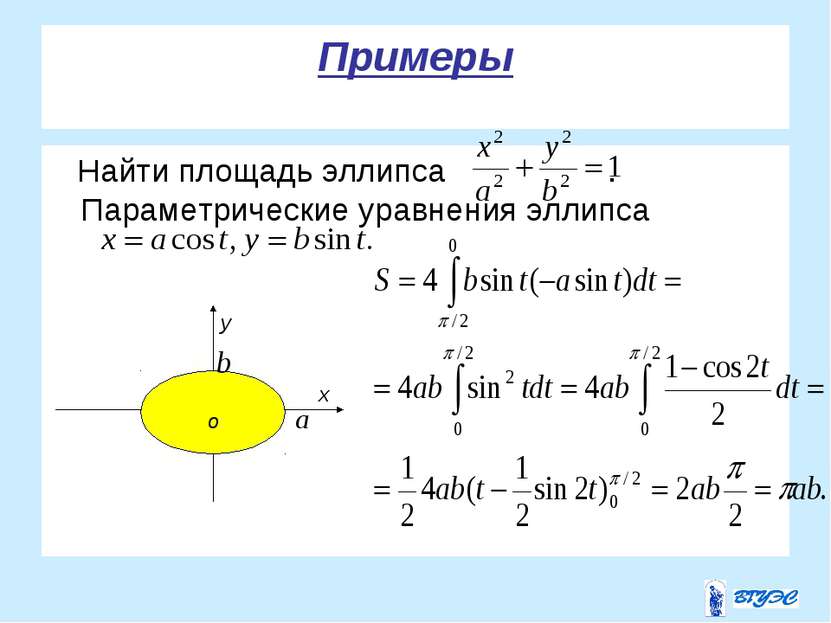
 Вычисление площадей В случае параметрического задания кривой, площадь фигуры, ограниченной прямыми , осью Ох и кривой вычисляют по формуле где пределы интегрирования определяют из уравнений . .
Вычисление площадей В случае параметрического задания кривой, площадь фигуры, ограниченной прямыми , осью Ох и кривой вычисляют по формуле где пределы интегрирования определяют из уравнений . .
Cлайд 30
 Вычисление длины дуги Если кривая задана параметрическими уравнениями , , то длина ее дуги , где –значения параметра, соответствующие концам дуги .
Вычисление длины дуги Если кривая задана параметрическими уравнениями , , то длина ее дуги , где –значения параметра, соответствующие концам дуги .
Cлайд 31
 Длина дуги в декартовых координатах Если кривая задана уравнением , то , где a, b–абсциссы начала и конца дуги . Если кривая задана уравнением , то , где c, d–ординаты начала и конца дуги
Длина дуги в декартовых координатах Если кривая задана уравнением , то , где a, b–абсциссы начала и конца дуги . Если кривая задана уравнением , то , где c, d–ординаты начала и конца дуги
Cлайд 32
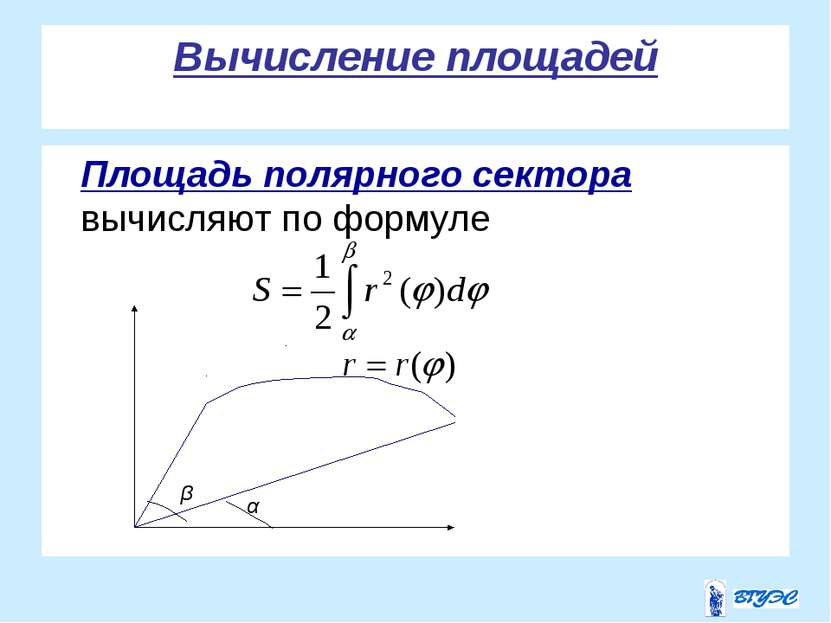
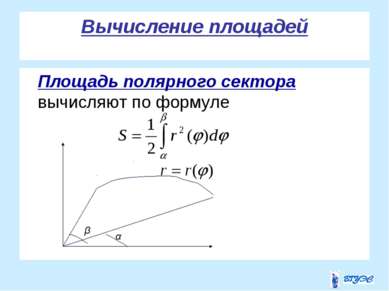
 Длина дуги в полярных координатах Если кривая задана уравнением в полярных координатах , то , где –значения полярного угла, соответствующие концам дуги .
Длина дуги в полярных координатах Если кривая задана уравнением в полярных координатах , то , где –значения полярного угла, соответствующие концам дуги .
Cлайд 34
 Вычисление объема тела вращения. Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой , отрезком оси абсцисс и прямыми , вычисляется по формуле .
Вычисление объема тела вращения. Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой , отрезком оси абсцисс и прямыми , вычисляется по формуле .
Cлайд 35
 Вычисление объема тела вращения Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком оси ординат и прямыми , вычисляется по формуле .
Вычисление объема тела вращения Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком оси ординат и прямыми , вычисляется по формуле .