X
Код презентации скопируйте его
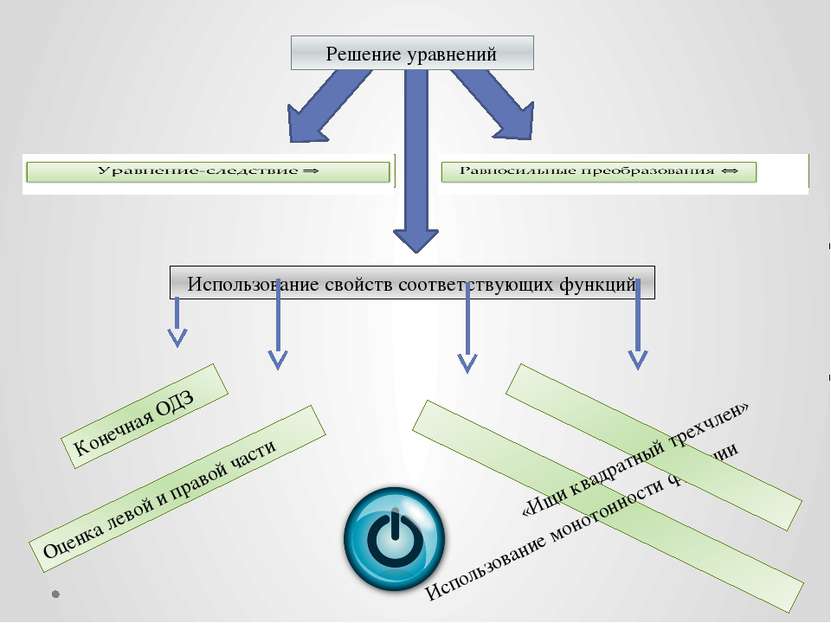
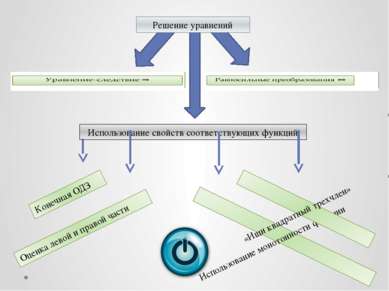
Решение уравнений
Скачать эту презентацию
Презентация на тему Решение уравнений
Скачать эту презентациюCлайд 1
Ответ: 3. = 2 > 0, > 0, ≠ 1, ОДЗ Равносильные преобразования
Cлайд 2
1. Подбираем один или несколько корней уравнения. 2. Доказываем, что других корней это уравнение не имеет Ответ: х=2
Cлайд 3
Ответ: 1.
Cлайд 4
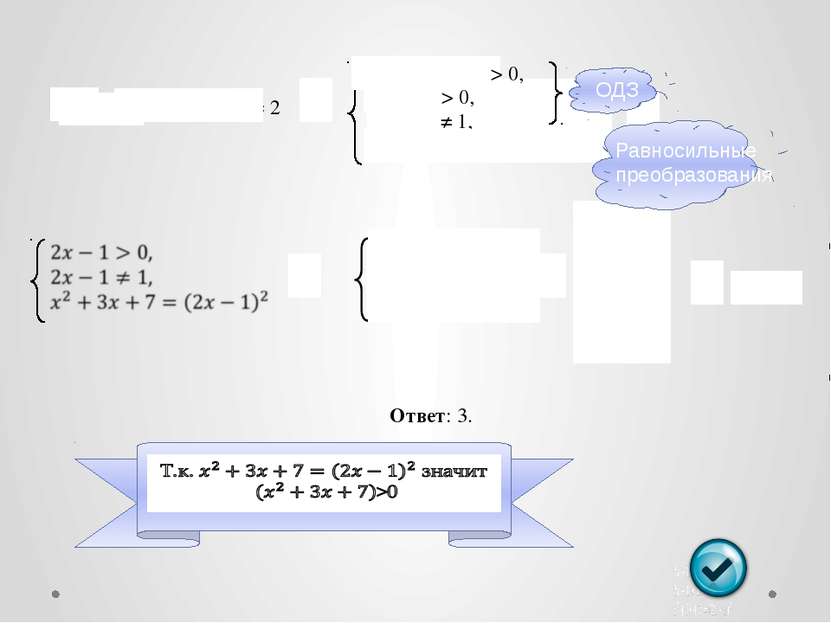
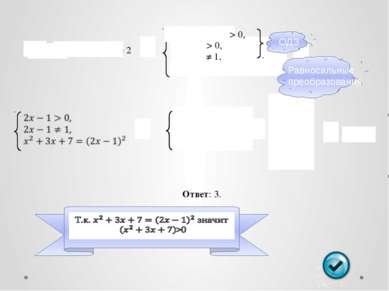
СХЕМА ВЫПОЛНЕНИЯ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ УРАВНЕНИЙ Учесть ОДЗ исходного уравнения Гарантировать (на ОДЗ) прямые и обратные преобразования Пример:
Cлайд 5
Решение: Ответ: х=2 Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
Cлайд 6
Конечная ОДЗ Если область допустимых значений (ОДЗ) уравнения (или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения У некоторых уравнений область определения состоит только из конечного числа точек. Для решения таких уравнений достаточно проверить, не являются ли найденные числа из области определения уравнения корнями этого уравнения. Пример:
Cлайд 7
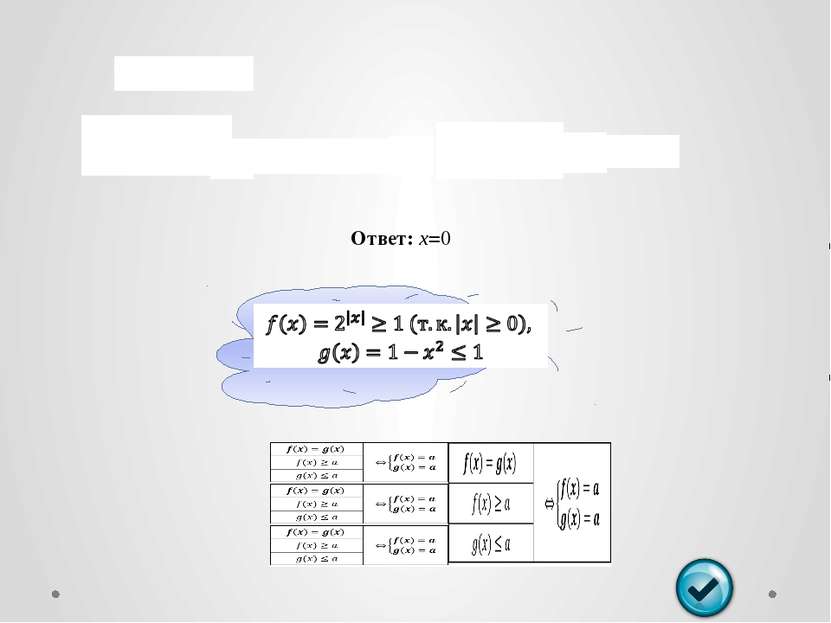
Оценка левой и правой части уравнения Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Пример: Пример:
Cлайд 8
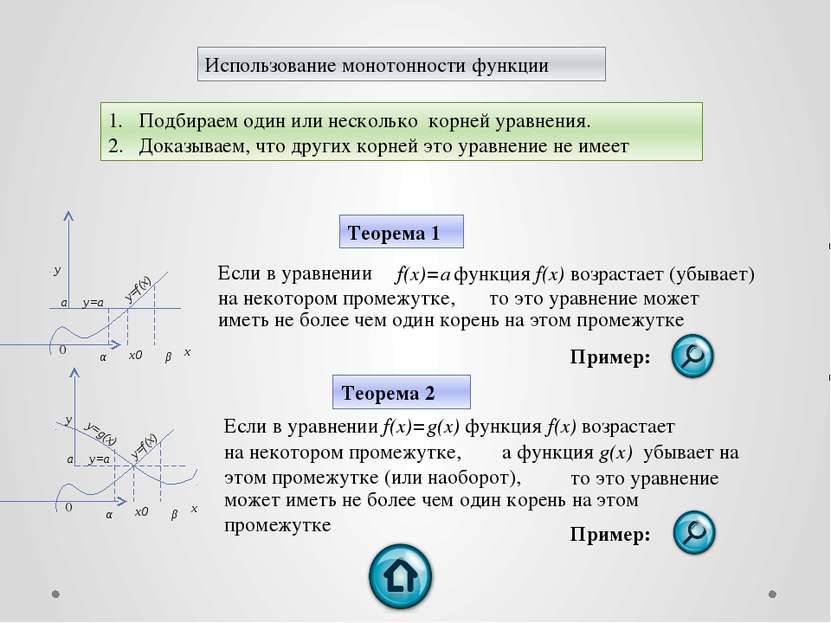
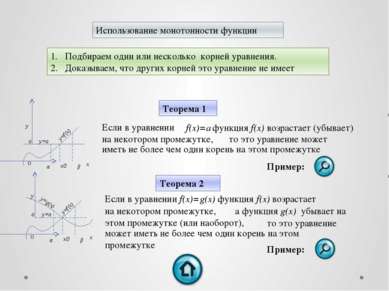
Использование монотонности функции Подбираем один или несколько корней уравнения. Доказываем, что других корней это уравнение не имеет x α β x0 a y=a y=f(x) 0 x α β x0 a y=a y=f(x) 0 y=g(x) Если в уравнении f(x)=a функция f(x) возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке y Теорема 1 y Теорема 2 Если в уравнении f(x)=g(x) функция f(x) возрастает на некотором промежутке, а функция g(x) убывает на то это уравнение этом промежутке (или наоборот), может иметь не более чем один корень на этом промежутке Пример: Пример:
Cлайд 9
«Ищи квадратный трёхчлен» Попробуйте рассмотреть данное уравнение как квадратное относительно какой-либо переменной (или какой-либо функции) Решение:
Cлайд 10
Используемая литература Е.П.Нелин Алгебра в таблицах 7-11, «Определения, свойства, методы решения задач в таблицах»; Е.П.Нелин Методы решения алгебраических задач (приложение к учебному пособию «Алгебра в таблицах»)
Cлайд 11
Используемые иллюстрации Е.П.Нелин Алгебра в таблицах 7-11, «Определения, свойства, методы решения задач в таблицах»; Office.com – кнопки для навигации по сайту.
Cлайд 12
Cлайд 13
Cлайд 14
Cлайд 15
Cлайд 16
Cлайд 17
