X
Код презентации скопируйте его
Правильная пирамида
Скачать эту презентацию
Презентация на тему Правильная пирамида
Скачать эту презентациюCлайд 1
Правильная пирамида Выполнила Петренко Наталья Викторовна, Учитель математики МОУ СОШ №7, Ст.Воронежской, Усть - Лабинского района, Краснодарского края http://aida.ucoz.ru
Cлайд 2
A D C B O K T E 2 http://aida.ucoz.ru
Cлайд 3
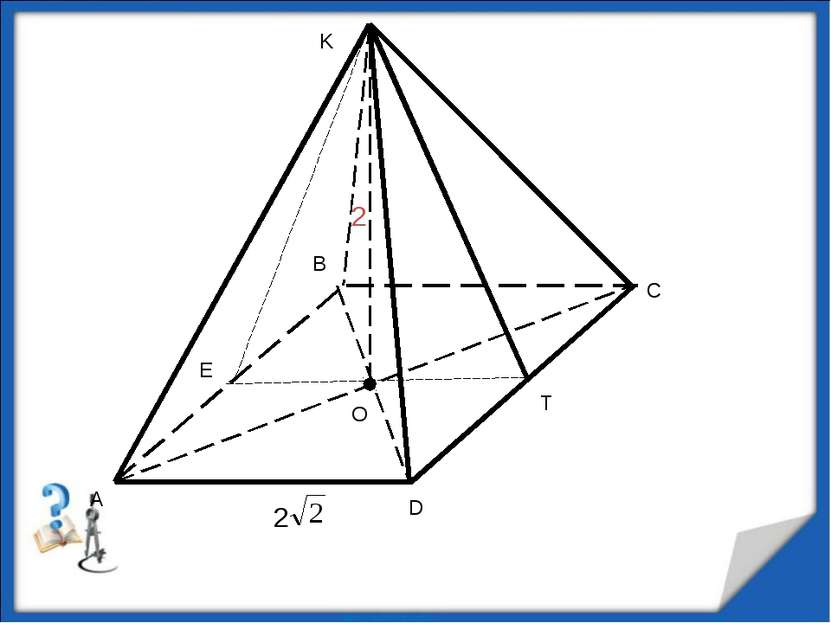
В правильной четырехугольной пирамиде известны длина стороны основания 2 и длина высоты 2. Найдите: а) объем пирамиды; б) площадь боковой по верхности; в) угол наклона бокового ребра к плоскости основания; г) угол наклона боковой грани к плоскости основания; д) радиус вписанного шара; е) радиус описанного шара; ж) расстояние от вершины пирамиды до плоскости основания; http://aida.ucoz.ru
Cлайд 4
з) расстояние от вершины пирамиды до ребра основания; и) расстояние от ребра основания до противоположной грани; к) расстояние между боковым ребром и скрещивающейся с ним диагональю ос нования; л) объем вписанного конуса; м) площадь боковой поверхности описанного конуса. Выход http://aida.ucoz.ru
Cлайд 5
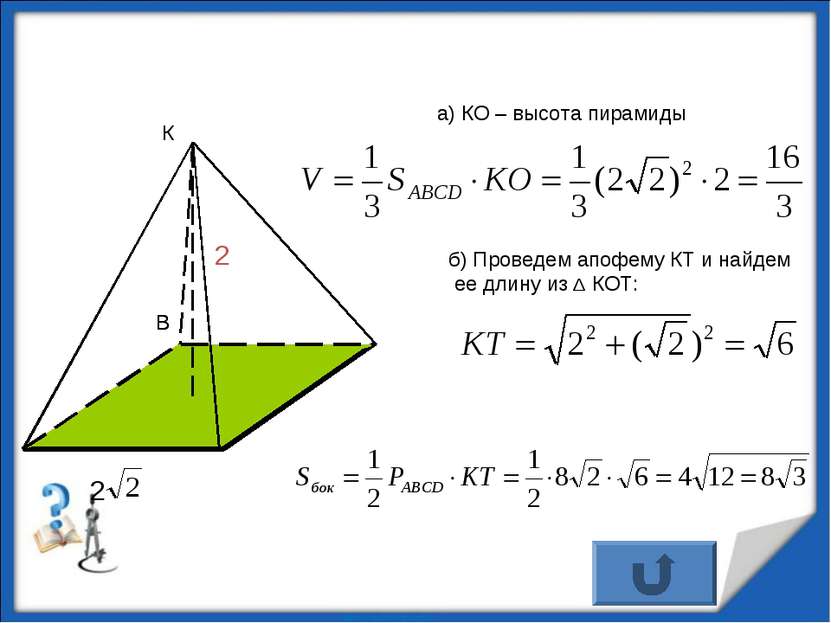
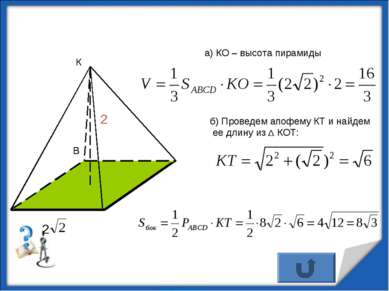а) КО – высота пирамиды В О К 2 б) Проведем апофему КТ и найдем ее длину из Δ КОТ: В http://aida.ucoz.ru
Cлайд 6
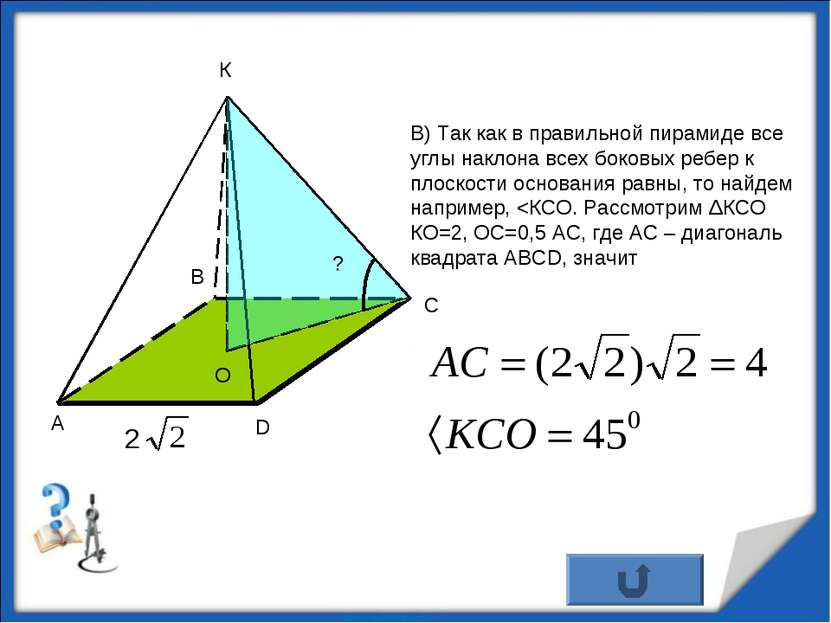
В) Так как в правильной пирамиде все углы наклона всех боковых ребер к плоскости основания равны, то найдем например,
Cлайд 7
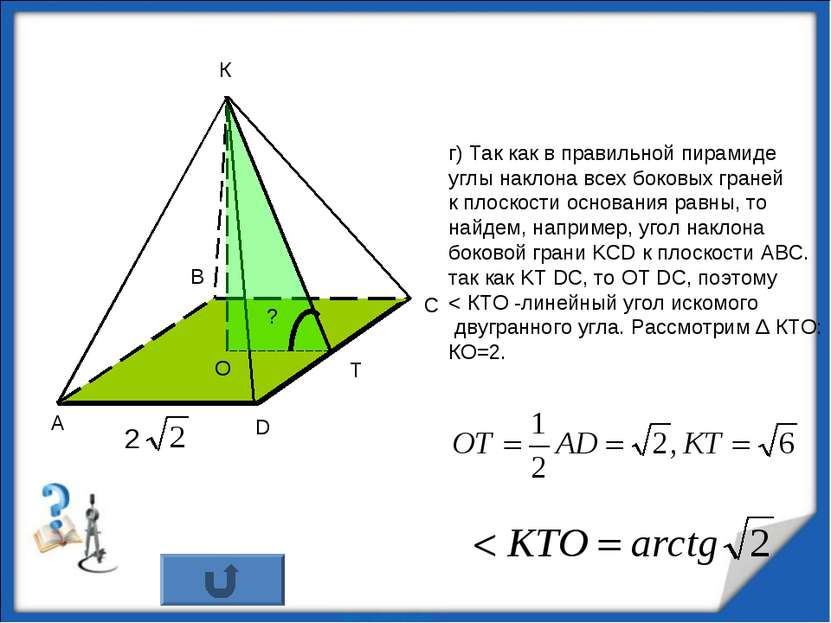
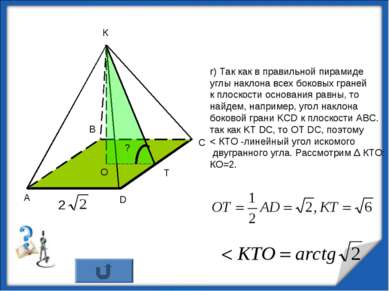г) Так как в правильной пирамиде углы наклона всех боковых граней к плоскости основания равны, то найдем, например, угол наклона боковой грани KCD к плоскости АВС. так как KT DC, то OT DC, поэтому < КТО -линейный угол искомого двугранного угла. Рассмотрим Δ КТО: КО=2. Т К О ? http://aida.ucoz.ru
Cлайд 8
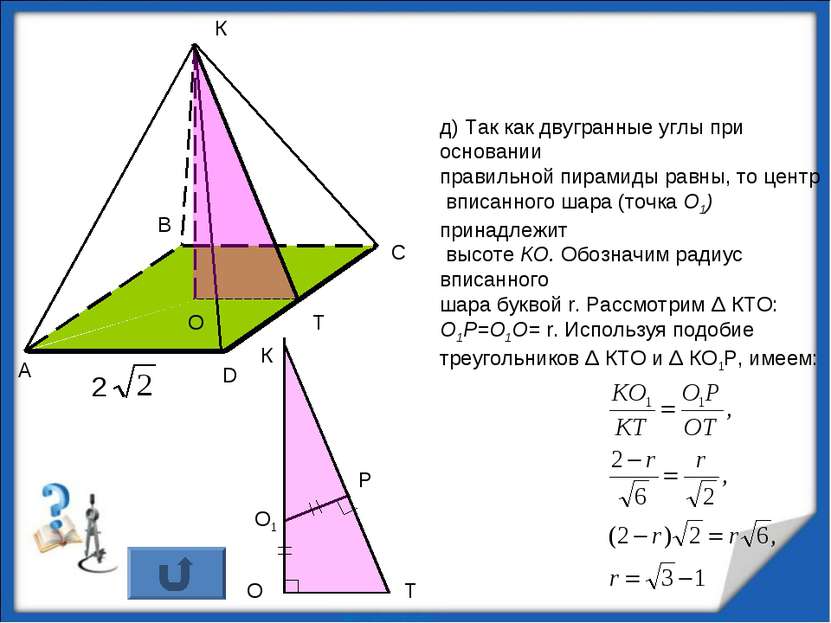
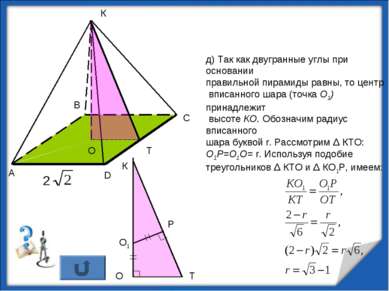д) Так как двугранные углы при основании правильной пирамиды равны, то центр вписанного шара (точка О1) принадлежит высоте КО. Обозначим радиус вписанного шара буквой r. Рассмотрим Δ КТО: О1Р=О1О= r. Используя подобие треугольников Δ КТО и Δ КО1Р, имеем: К Т О http://aida.ucoz.ru
Cлайд 9
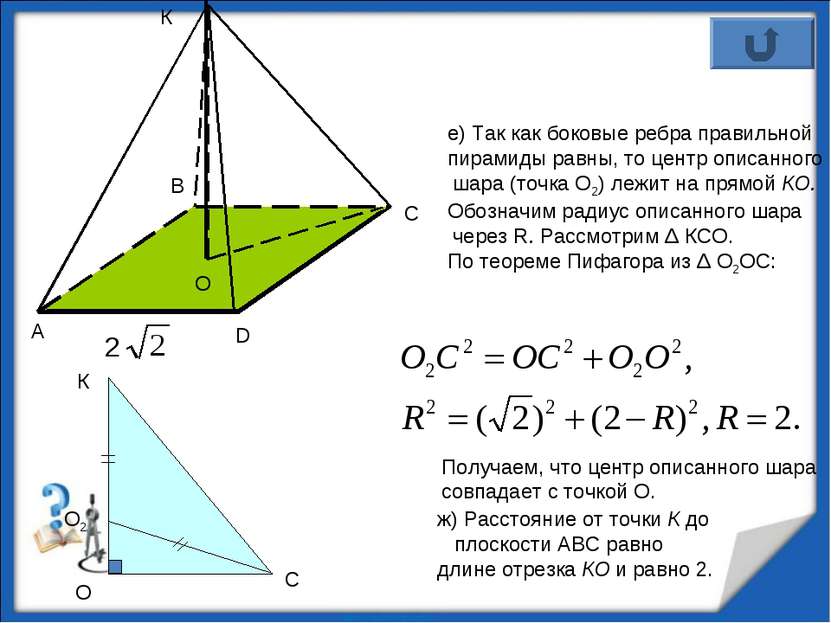
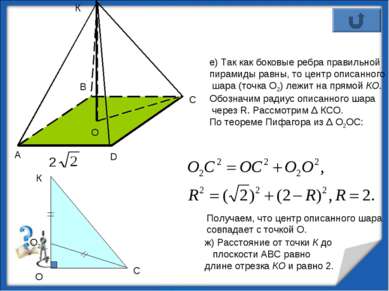е) Так как боковые ребра правильной пирамиды равны, то центр описанного шара (точка О2) лежит на прямой КО. Обозначим радиус описанного шара через R. Рассмотрим Δ КСО. По теореме Пифагора из Δ О2ОС: Получаем, что центр описанного шара совпадает с точкой О. К О О2 О К С ж) Расстояние от точки К до плоскости АВС равно длине отрезка КО и равно 2. http://aida.ucoz.ru
Cлайд 10
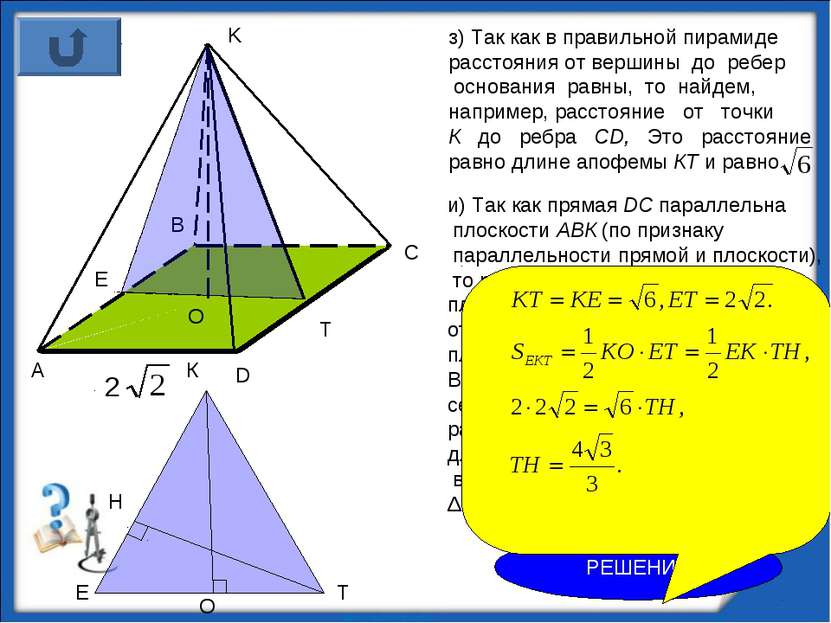
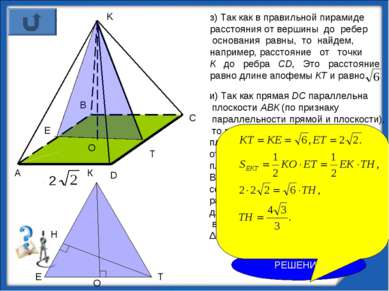з) Так как в правильной пирамиде расстояния от вершины до ребер основания равны, то найдем, например, расстояние от точки К до ребра СD, Это расстояние равно длине апофемы КТ и равно K O T и) Так как прямая DС параллельна плоскости АВК (по признаку параллельности прямой и плоскости), то расстояние от прямой DС до плоскости АВК равно расстоянию от любой точки прямой DС до этой плоскости. Рассмотрим на прямой ВС точку Т. И из Δ ЕКТ (точка Е — середина АВ) найдем искомое расстояние. Это расстояние равно длине высоты ТН. Найдем длину ТН, выразив двумя способами площадь Δ ЕКТ. Е РЕШЕНИЕ http://aida.ucoz.ru
Cлайд 11
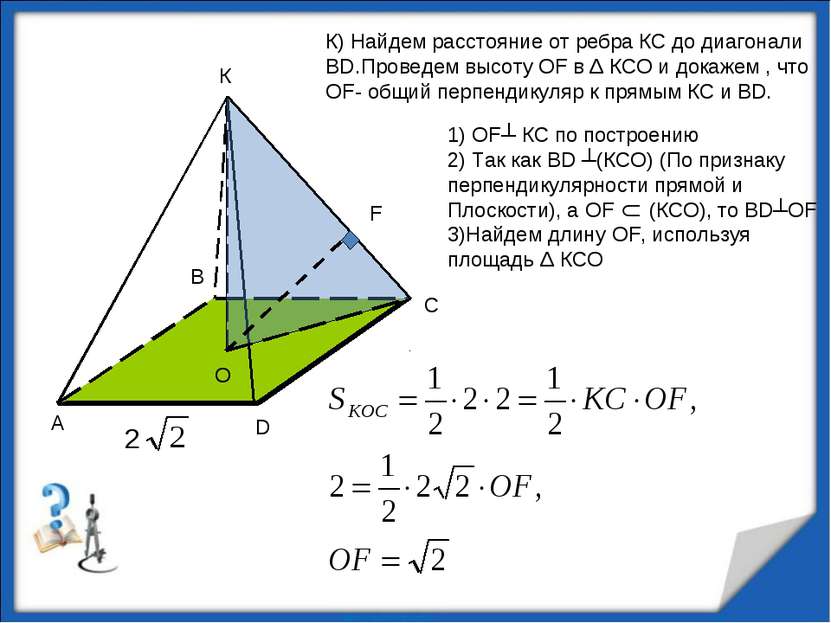
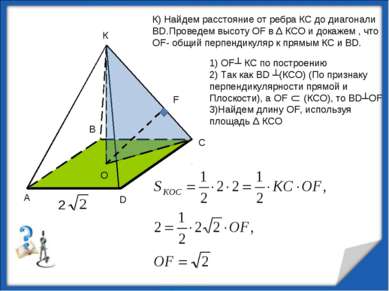К К) Найдем расстояние от ребра КС до диагонали ВD.Проведем высоту OF в Δ КСО и докажем , что OF- общий перпендикуляр к прямым КС и ВD. 1) OF┴ КС по построению 2) Так как ВD ┴(КСО) (По признаку перпендикулярности прямой и Плоскости), а OF (КСО), то ВD┴OF 3)Найдем длину OF, используя площадь Δ КСО О F http://aida.ucoz.ru
Cлайд 12
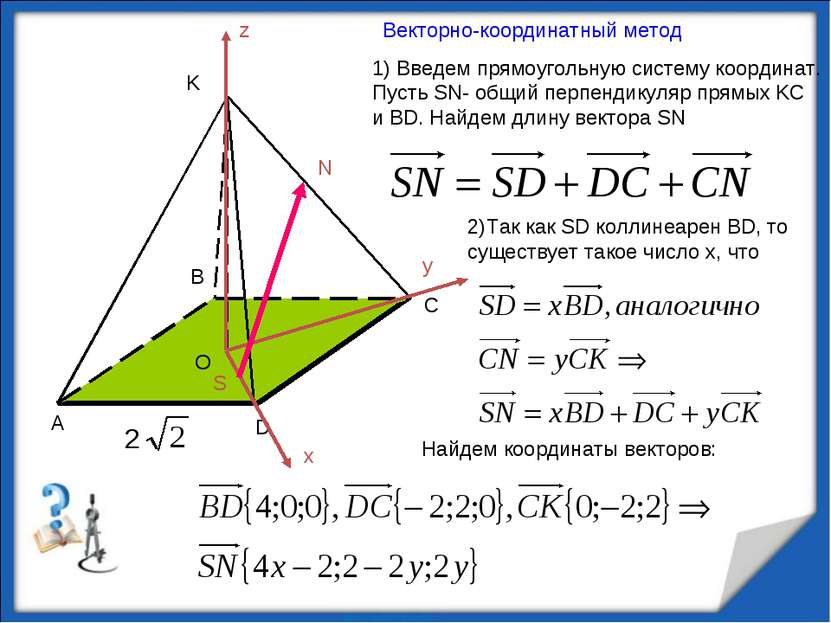
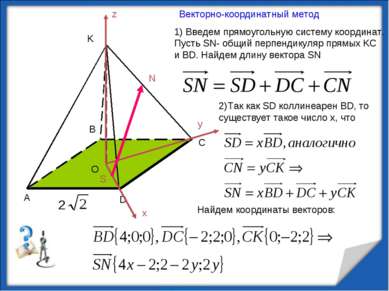1) Введем прямоугольную систему координат. Пусть SN- общий перпендикуляр прямых KC и BD. Найдем длину вектора SN 2)Так как SD коллинеарен BD, то существует такое число х, что Найдем координаты векторов: Векторно-координатный метод z x y K O S N http://aida.ucoz.ru
Cлайд 13
http://aida.ucoz.ru
Cлайд 14
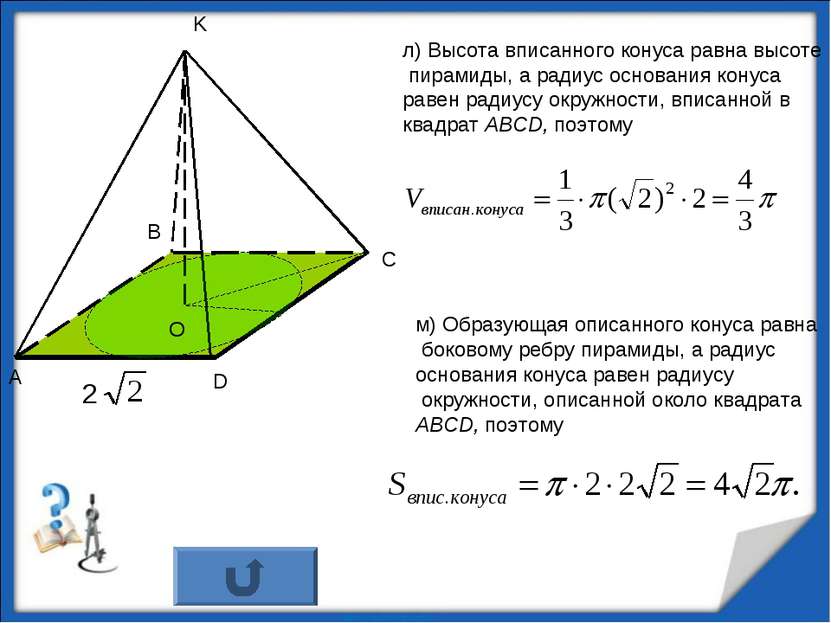
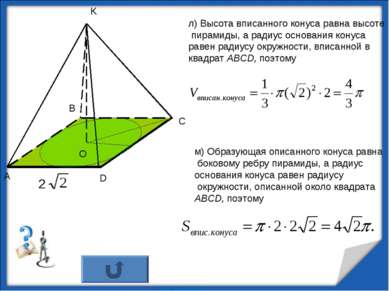л) Высота вписанного конуса равна высоте пирамиды, а радиус основания конуса равен радиусу окружности, вписанной в квадрат АВСD, поэтому м) Образующая описанного конуса равна боковому ребру пирамиды, а радиус основания конуса равен радиусу окружности, описанной около квадрата АВСD, поэтому K O http://aida.ucoz.ru
Cлайд 15
http://aida.ucoz.ru
