X
Код презентации скопируйте его
Пирамида (10 класс)
Скачать эту презентацию
Презентация на тему Пирамида (10 класс)
Скачать эту презентациюCлайд 1
Урок математики в 10 классе по теме «Пирамида» подготовила учитель математики первой категории Идиятуллина А.М МБОУ «СОШ№22 с углубленным изучением английского языка» г.Нижнекамска РТ
Cлайд 2
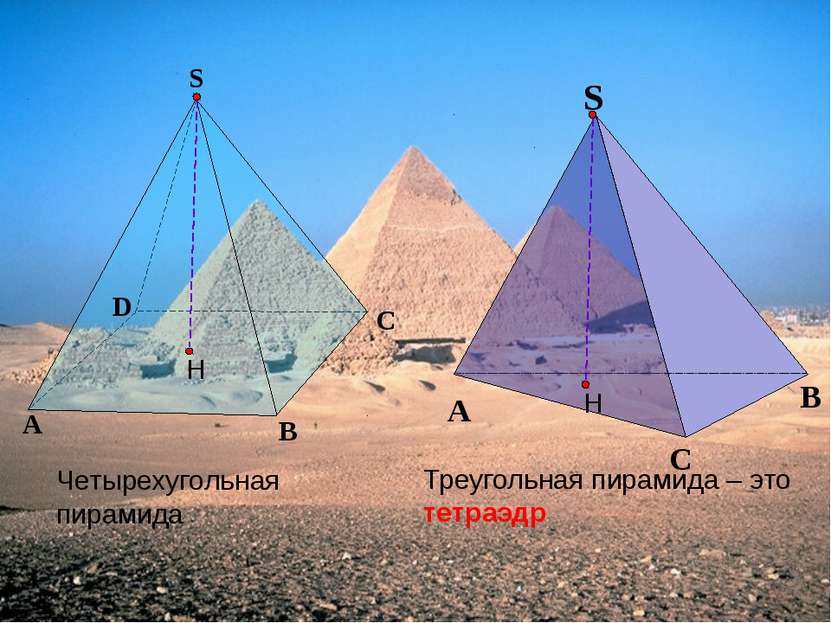
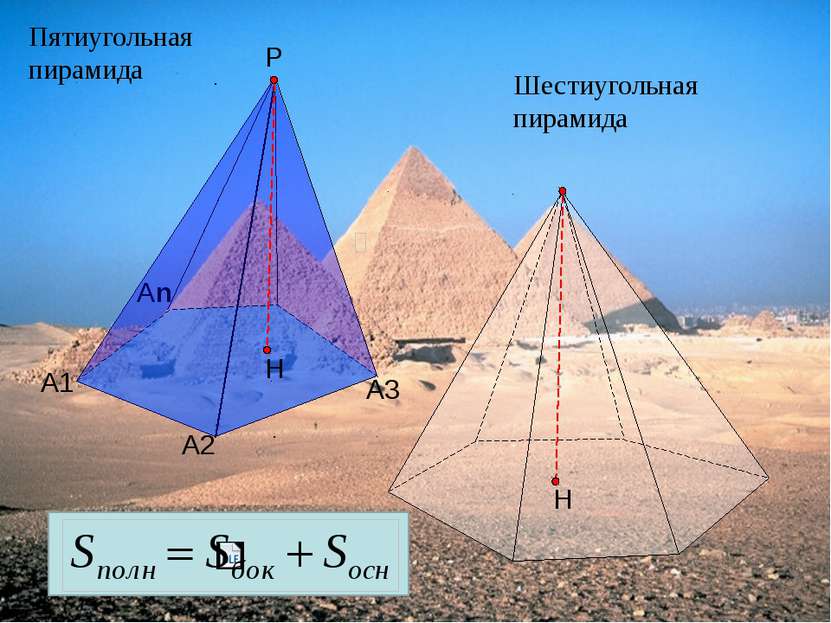
Содержание Определение пирамиды Правильная пирамида Усеченная пирамида Решение задач Итог урока Список литературы
Cлайд 3
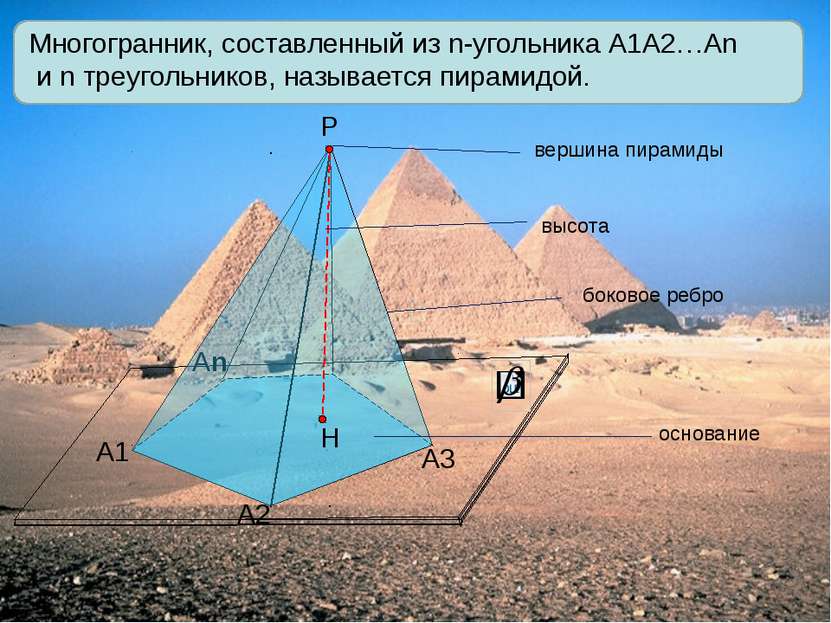
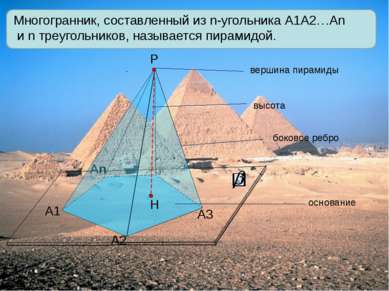А1 А2 Аn Р А3 Многогранник, составленный из n-угольника А1А2…Аn и n треугольников, называется пирамидой. вершина пирамиды высота боковое ребро основание Н
Cлайд 4
Треугольная пирамида – это тетраэдр Четырехугольная пирамида А B C D S С А В S Н Н
Cлайд 5
Пятиугольная пирамида А1 А2 Аn Р А3 Шестиугольная пирамида Н Н
Cлайд 6
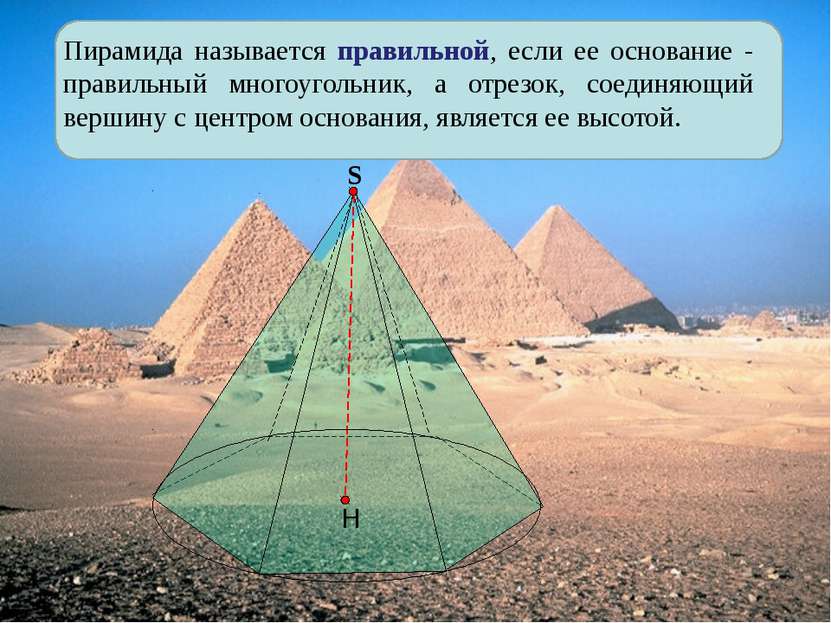
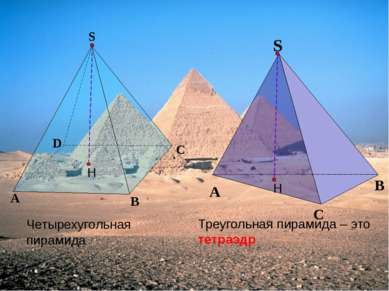
Пирамида называется правильной, если ее основание - правильный многоугольник, а отрезок, соединяющий вершину с центром основания, является ее высотой. S
Cлайд 7
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. А1 А2 А3 А4 А5 А6 S Н
Cлайд 8
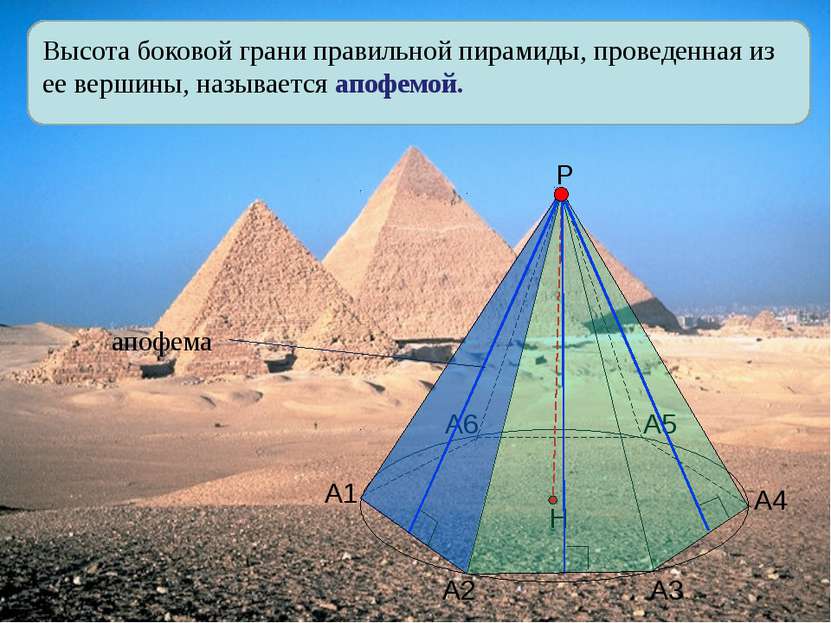
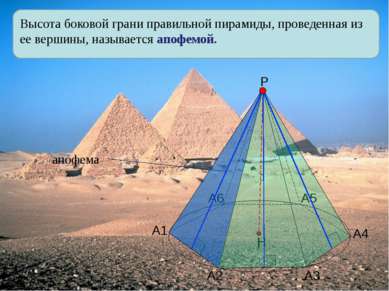Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. А1 А2 А3 А4 А5 А6 Р апофема Н
Cлайд 9
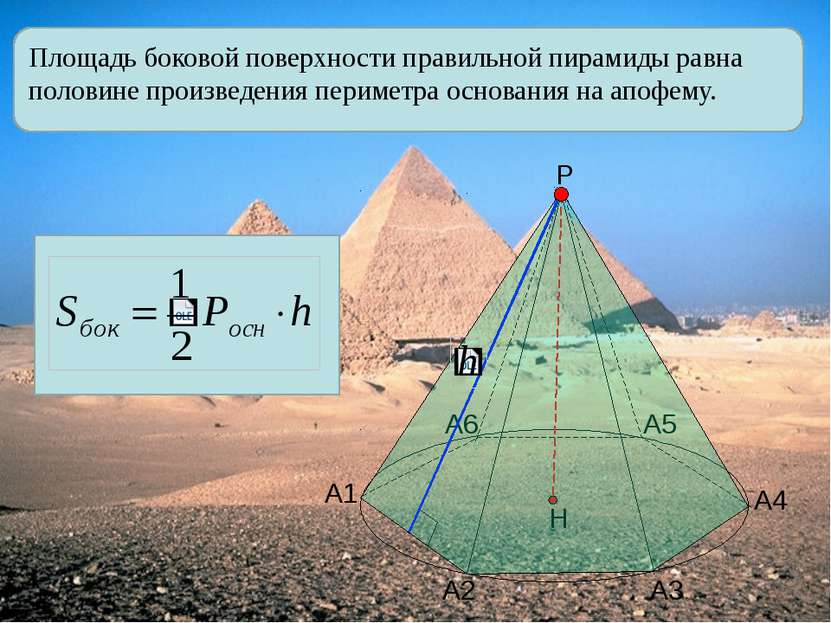
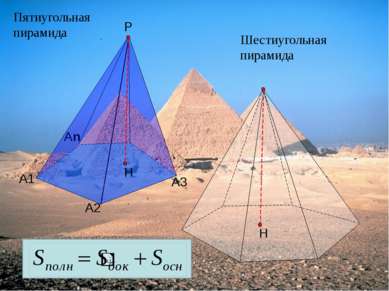
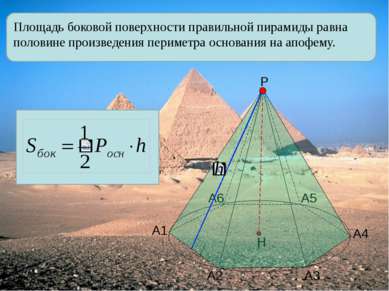Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. А1 А2 А3 А4 А5 А6 Р Н
Cлайд 10
А1 А2 Аn А3 Усеченная пирамида Р В1 В2 В3
Cлайд 11
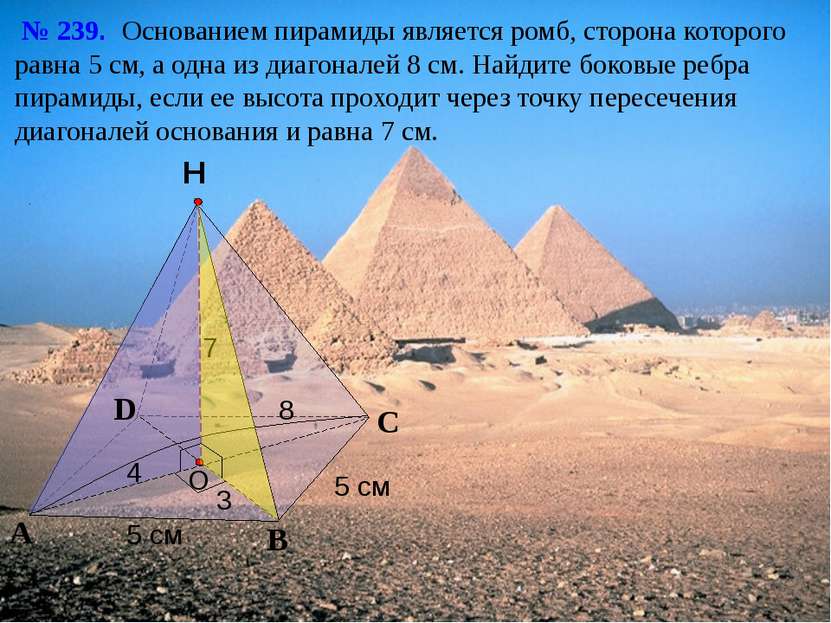
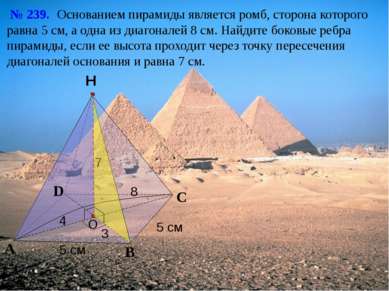С А В Н № 239. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей 8 см. Найдите боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см. O D 5 см 5 см 7 4 3 8
Cлайд 12
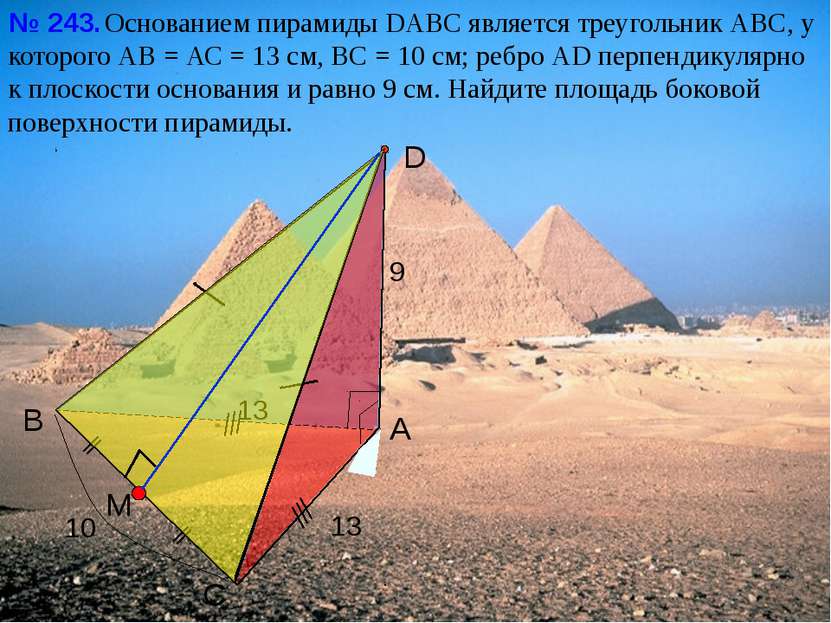
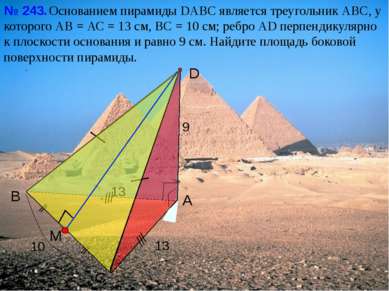С В А D Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13 см, ВС = 10 см; ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды. № 243. 13 9 10 13 M Л.С. Атанасян «Геометрия 10-11»
Cлайд 13
Что называется пирамидой? Правильной пирамидой? Что называется площадью боковой поверхности пирамиды? Что называется площадью полной поверхности пирамиды? Чему равна площадь боковой поверхности правильной пирамиды? Как найти радиусы вписанной и описанной окружностей для произвольного треугольника? Формула для площади треугольника? Итог урока
Cлайд 14
Подведение итогов. Домашнее задание. П.32,33,34 №241,242
Cлайд 15
Список литературы Атанасян Л.С., Бутузов В.Ф.и др.Геометрия 10-11,Москва «Просвещение»,2010 Яровенко В.А. Поурочные разработки по геометрии. Дифференцированный подход. Москва «Вако»,2011
