X
Код презентации скопируйте его
Многогранник
Скачать эту презентацию
Презентация на тему Многогранник
Скачать эту презентациюCлайд 1
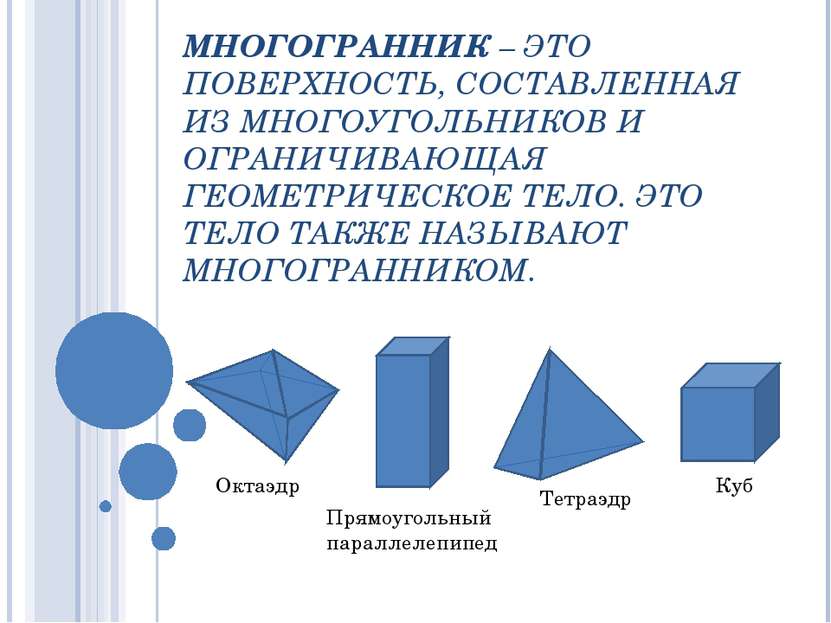
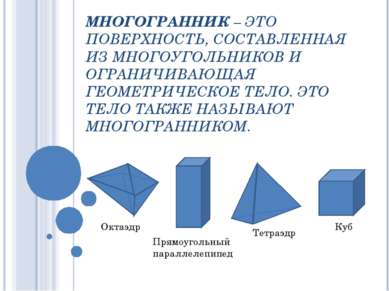МНОГОГРАННИК – ЭТО ПОВЕРХНОСТЬ, СОСТАВЛЕННАЯ ИЗ МНОГОУГОЛЬНИКОВ И ОГРАНИЧИВАЮЩАЯ ГЕОМЕТРИЧЕСКОЕ ТЕЛО. ЭТО ТЕЛО ТАКЖЕ НАЗЫВАЮТ МНОГОГРАННИКОМ. Октаэдр Прямоугольный параллелепипед Тетраэдр Куб
Cлайд 2
МНОГОГРАННИКИ Многоугольники, из которых составлен многогранник, называются гранями. Стороны граней называются рёбрами. А концы рёбер называют вершинами многоугольника. Гранью куба является квадрат А В АВ является ребром куба А А является вершиной куба
Cлайд 3
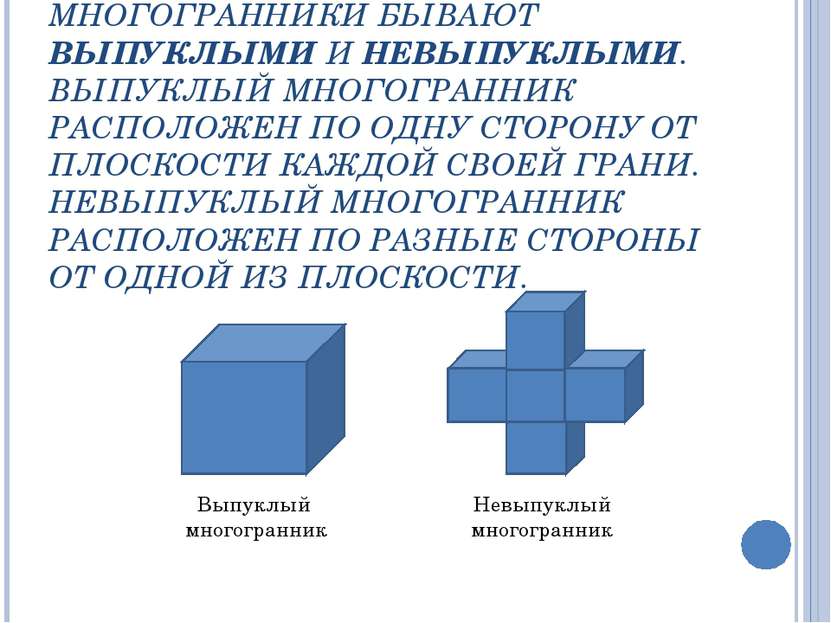
МНОГОГРАННИКИ БЫВАЮТ ВЫПУКЛЫМИ И НЕВЫПУКЛЫМИ. ВЫПУКЛЫЙ МНОГОГРАННИК РАСПОЛОЖЕН ПО ОДНУ СТОРОНУ ОТ ПЛОСКОСТИ КАЖДОЙ СВОЕЙ ГРАНИ. НЕВЫПУКЛЫЙ МНОГОГРАННИК РАСПОЛОЖЕН ПО РАЗНЫЕ СТОРОНЫ ОТ ОДНОЙ ИЗ ПЛОСКОСТИ. Выпуклый многогранник Невыпуклый многогранник
Cлайд 4
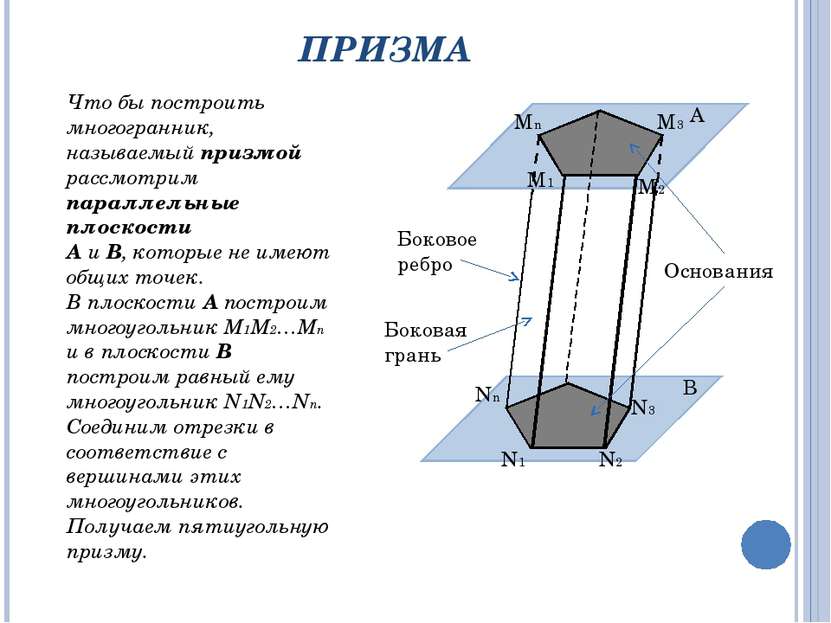
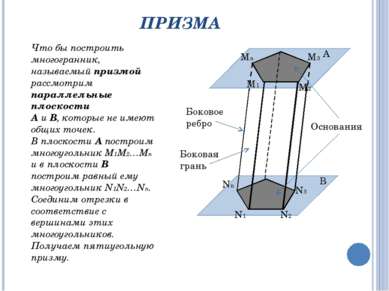ПРИЗМА Что бы построить многогранник, называемый призмой рассмотрим параллельные плоскости А и В, которые не имеют общих точек. В плоскости А построим многоугольник М1М2…Мn и в плоскости В построим равный ему многоугольник N1N2…Nn. Соединим отрезки в соответствие с вершинами этих многоугольников. Получаем пятиугольную призму. А В M1 M2 M3 Mn Nn N1 N2 N3 Боковое ребро Боковая грань Основания
Cлайд 5
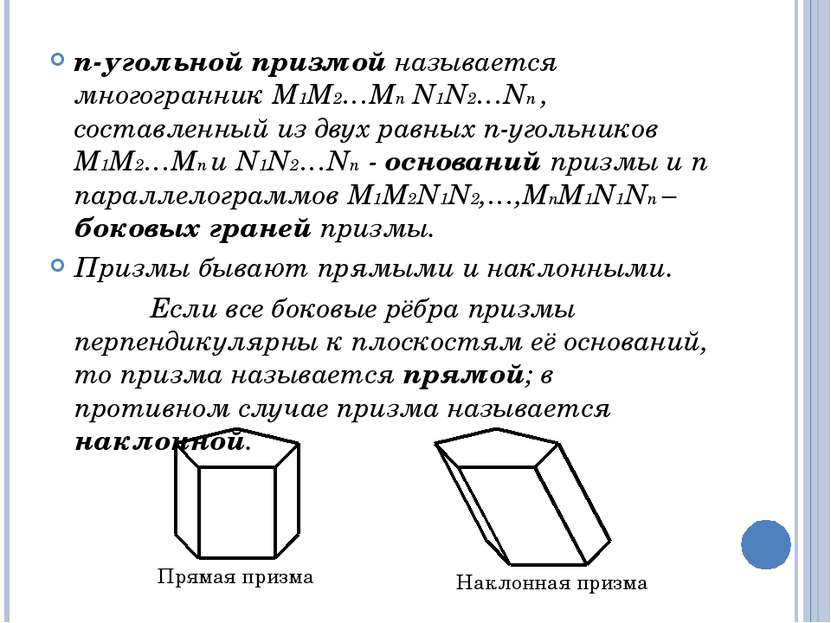
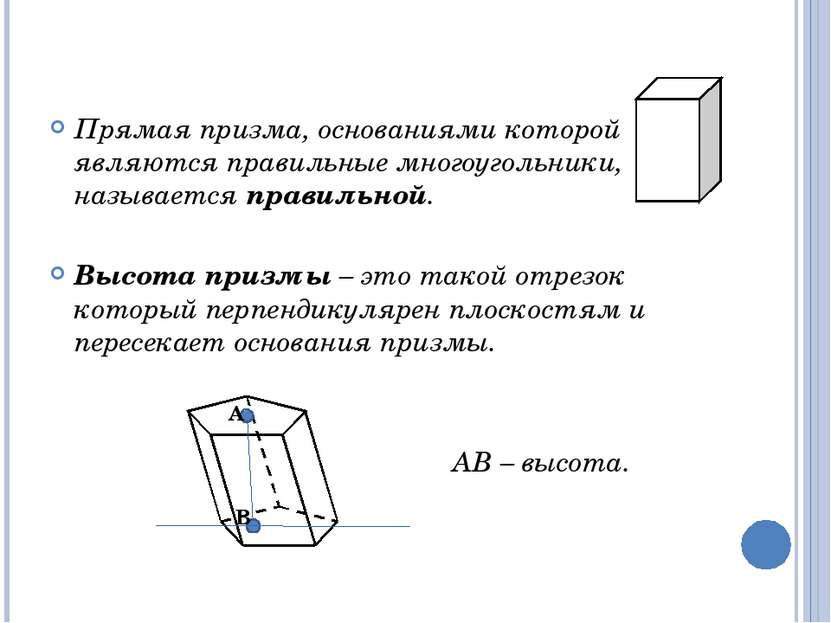
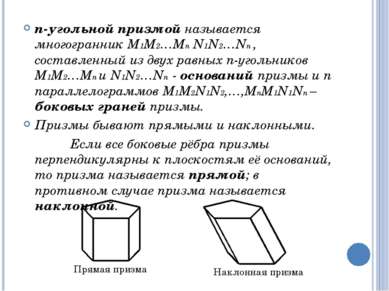n-угольной призмой называется многогранник М1М2…Мn N1N2…Nn , составленный из двух равных n-угольников М1М2…Мn и N1N2…Nn - оснований призмы и n параллелограммов М1М2N1N2,…,МnМ1N1Nn – боковых граней призмы. Призмы бывают прямыми и наклонными. Если все боковые рёбра призмы перпендикулярны к плоскостям её оснований, то призма называется прямой; в противном случае призма называется наклонной. Прямая призма Наклонная призма
Cлайд 6
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной. Высота призмы – это такой отрезок который перпендикулярен плоскостям и пересекает основания призмы. АВ – высота. А В
Cлайд 7
КОНЕЦ
