X
Код презентации скопируйте его
Многогранники вокруг нас
Скачать эту презентацию
Презентация на тему Многогранники вокруг нас
Скачать эту презентациюCлайд 1
Многогранники вокруг нас Самохвалова Т.М
Cлайд 2
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства. Бертран Рассел
Cлайд 3
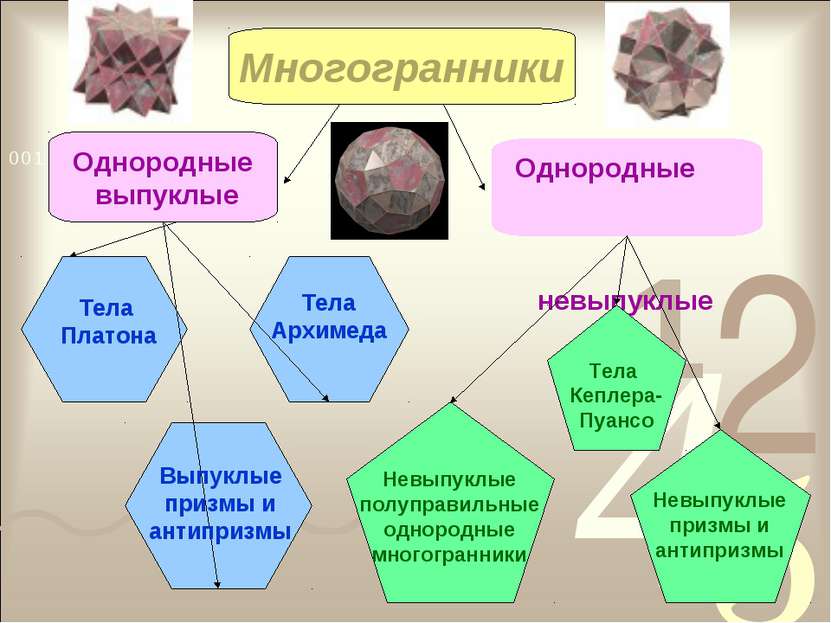
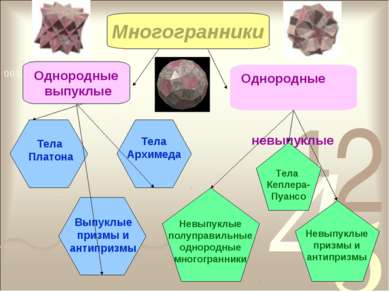Многогранники Однородные выпуклые Однородные невыпуклые Тела Архимеда Тела Платона Выпуклые призмы и антипризмы Тела Кеплера- Пуансо Невыпуклые полуправильные однородные многогранники Невыпуклые призмы и антипризмы
Cлайд 4
Правильными многогранниками Называют выпуклые многогранники, все грани и все углы которых равны, причём грани – правильные многоугольники. В каждой вершине правильного многогранника сходится одно и то же число рёбер. Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны. Правильные многогранники - трёхмерный аналог плоских правильных многоугольников.
Cлайд 5
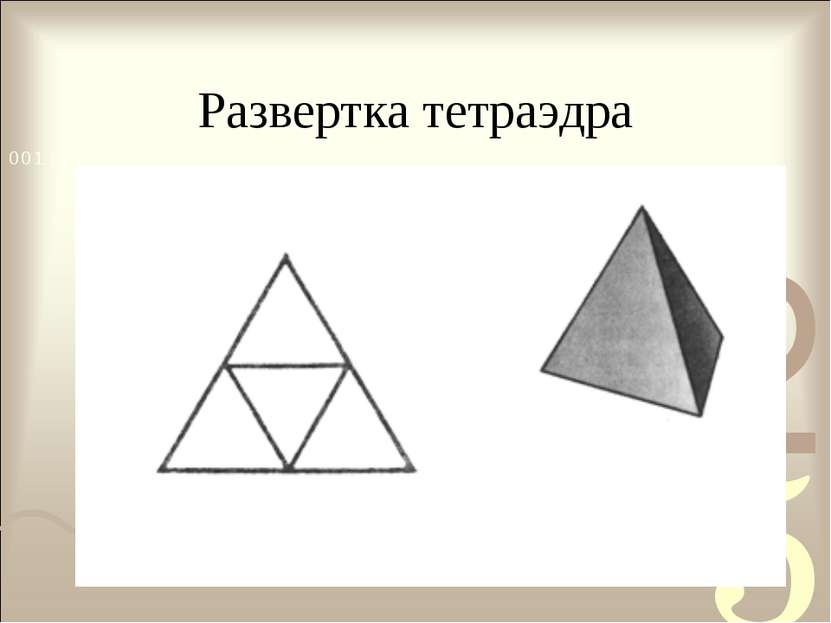
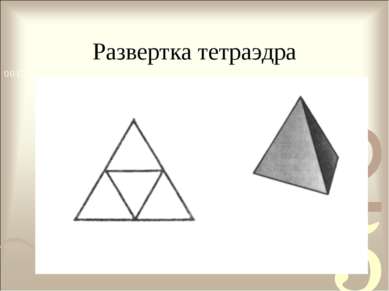
Правильные многогранники Сколько же их существует? Тетраэдр -правильная треугольная пирамида с равными ребрами, ограниченная четырьмя правильными треугольниками.
Cлайд 6
Развертка тетраэдра
Cлайд 7
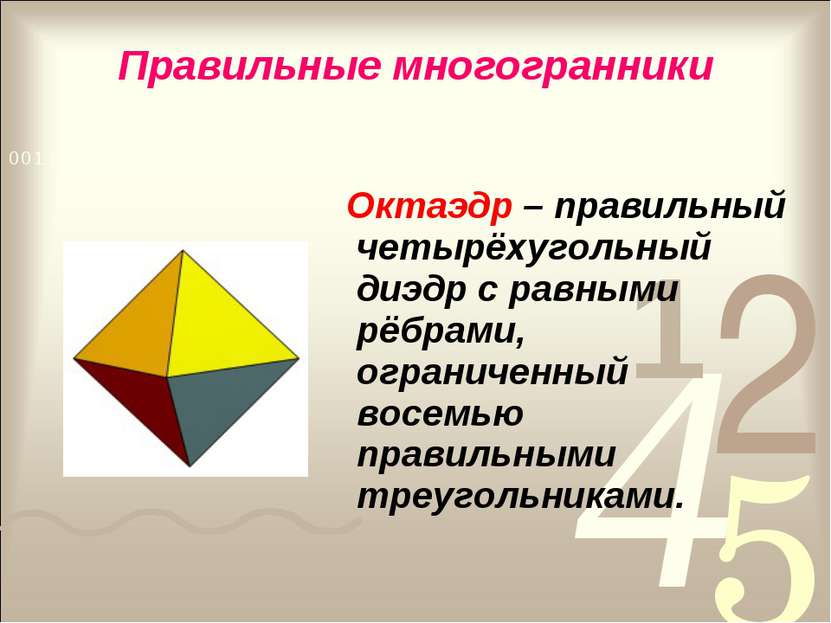
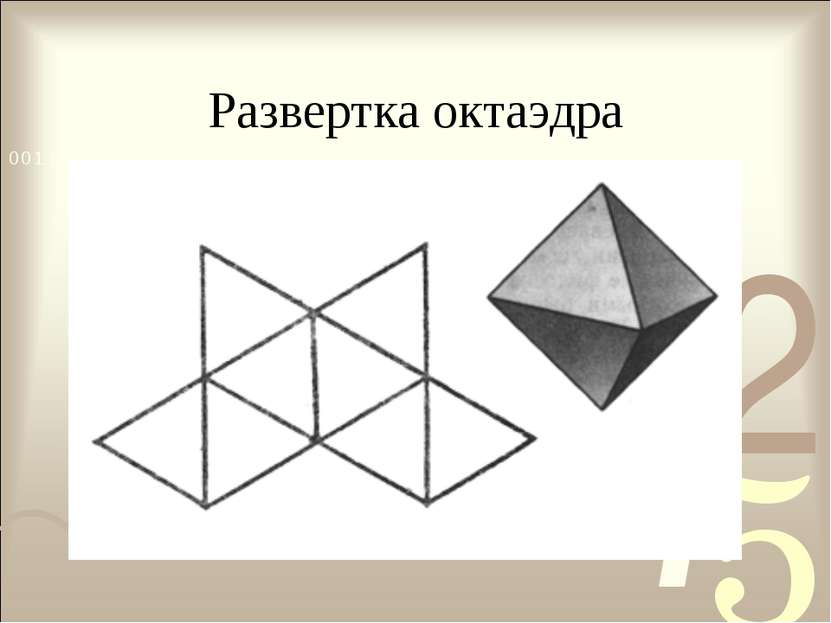
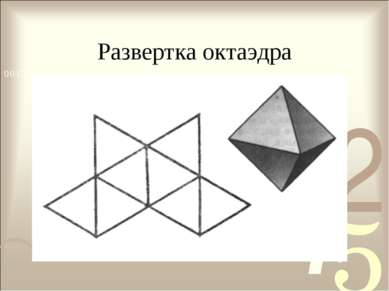
Правильные многогранники Октаэдр – правильный четырёхугольный диэдр с равными рёбрами, ограниченный восемью правильными треугольниками.
Cлайд 8
Развертка октаэдра
Cлайд 9
Развертка усеченного октаэдра
Cлайд 10
Развертка ромбоусеченного кубооктаэдра
Cлайд 11
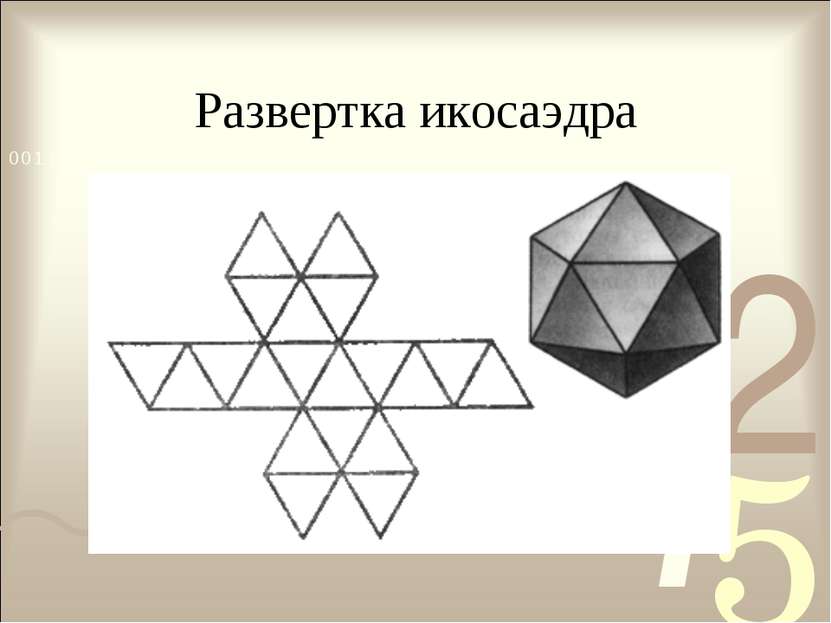
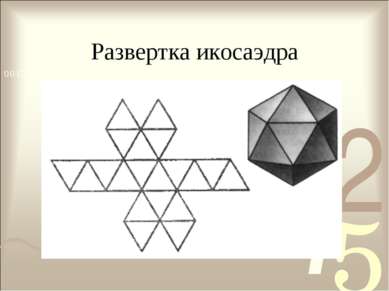
Икосаэдр- поверхность, ограниченная двадцатью правильными треугольниками. Правильные многогранники
Cлайд 12
Развертка икосаэдра
Cлайд 13
Куб(гексаэдр)- правильная четырёхугольная призма с равными рёбрами, ограниченная шестью квадратами. Правильные многогранники
Cлайд 14
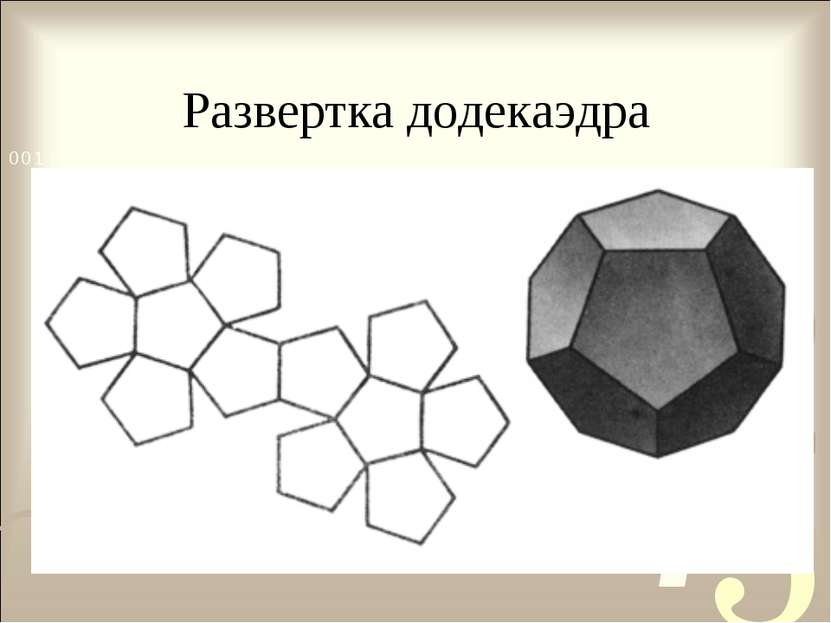
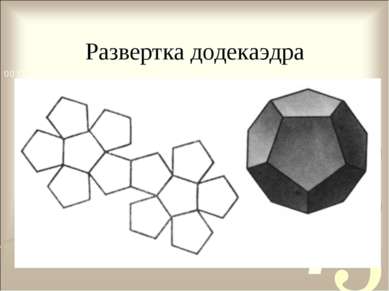
Правильные многогранники Додекаэдр- поверхность, ограниченная двенадцатью правильными пятиугольниками.
Cлайд 15
Развертка додекаэдра
Cлайд 16
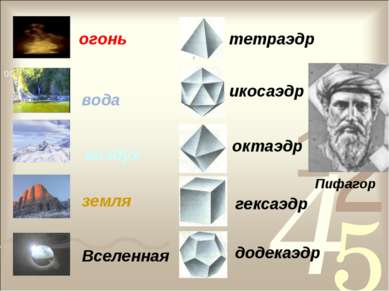
Сделаем вывод: Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Эти тела еще называют телами Платона.
Cлайд 17
Тетраэдр Икосаэдр Гексаэдр Додекаэдр Октаэдр
Cлайд 18
вода земля воздух огонь Вселенная додекаэдр гексаэдр октаэдр икосаэдр тетраэдр Пифагор
Cлайд 19
Двойственность куба и октаэдра
Cлайд 20
: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
Cлайд 21
Число вершин минус число ребер плюс число граней равно двум. Теорема Эйлера В – Р + Г = 2
Cлайд 22
Cлайд 23
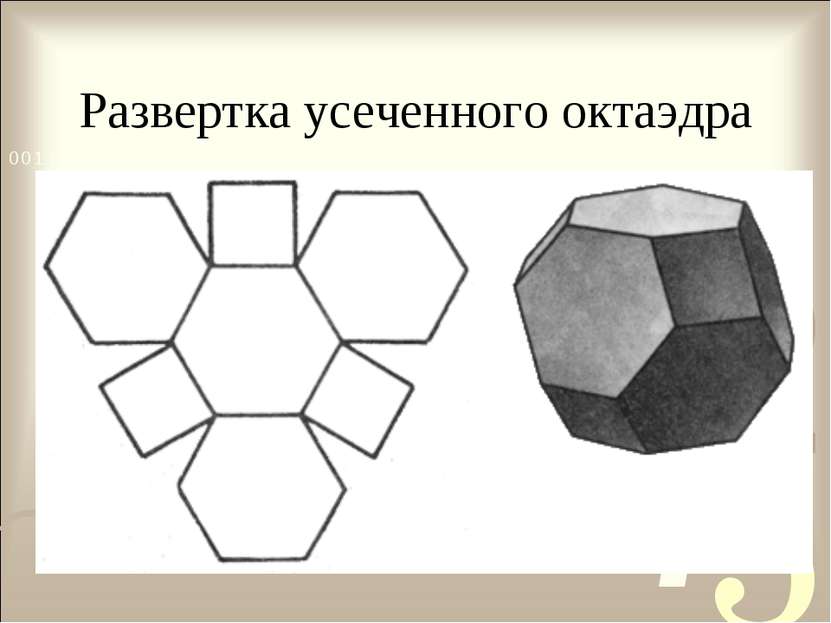
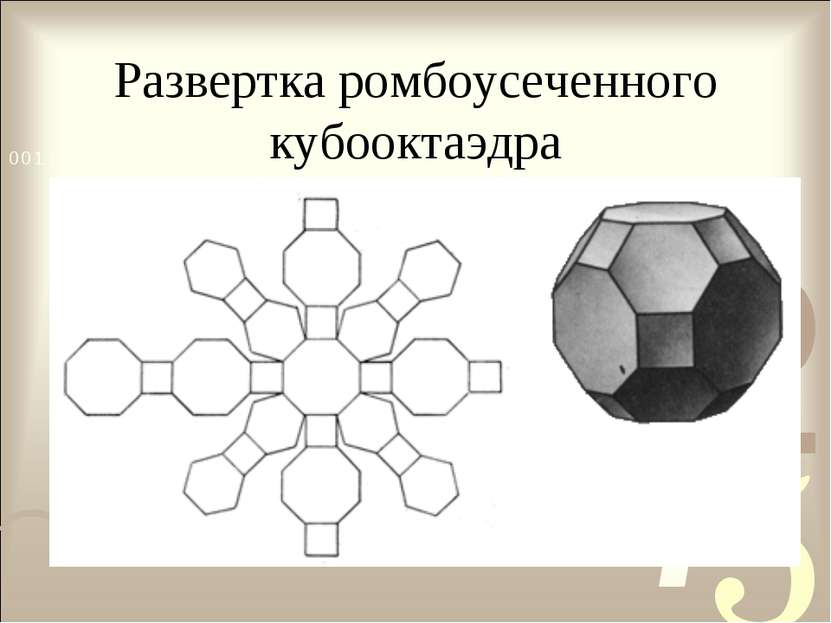
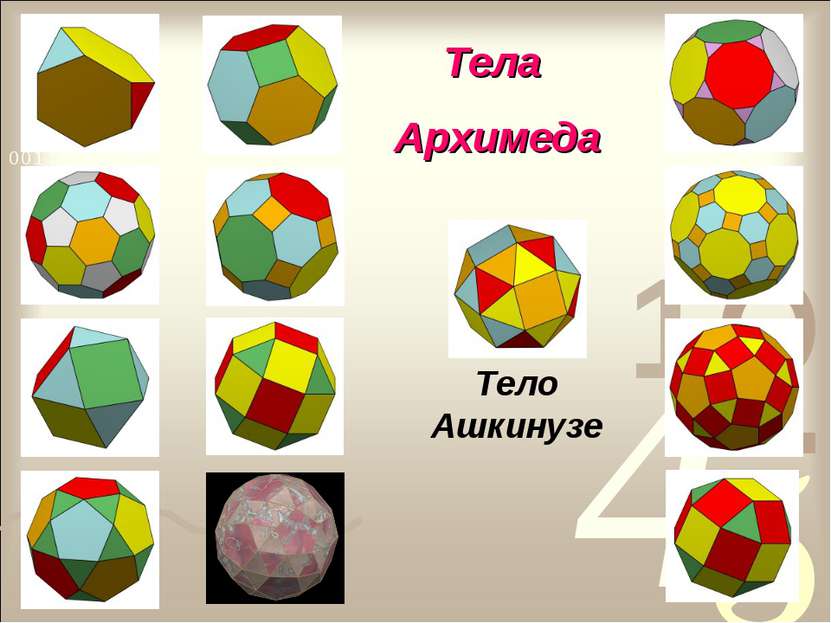
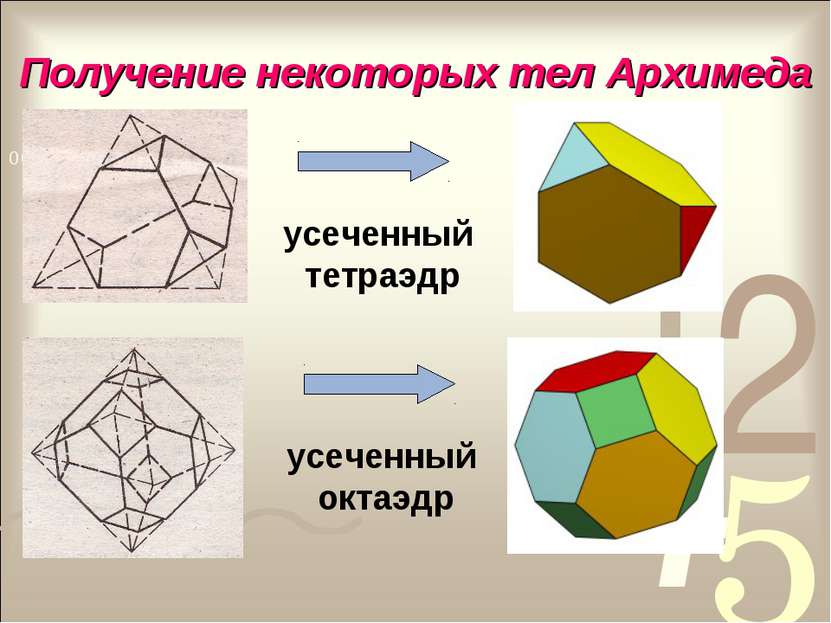
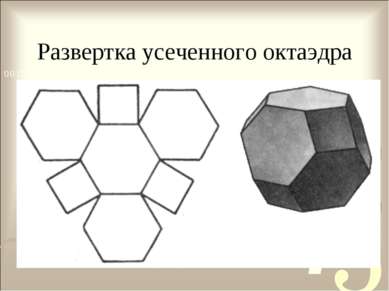
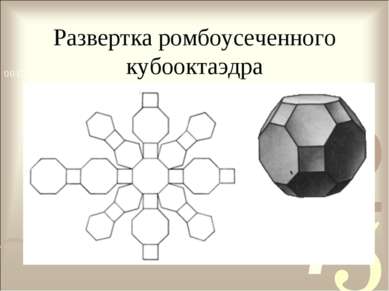
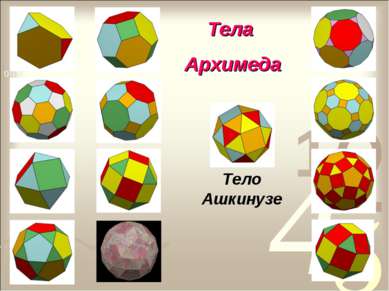
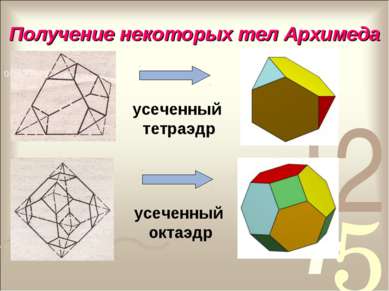
Тела Архимеда Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.
Cлайд 24
Тела Архимеда Тело Ашкинузе
Cлайд 25
Получение некоторых тел Архимеда усеченный тетраэдр усеченный октаэдр
Cлайд 26
Архимед (287-211 гг. до н.э.)
Cлайд 27
Кристаллы Халькопирит Топаз Пирит Авгит Медный купорос
Cлайд 28
Тела Кеплера – Пуансо (правильные звездчатые многогранники)
Cлайд 29
Большой звездчатый додекаэдр Большой икосаэдр Малый звездчатый додекаэдр Большой додекаэдр
Cлайд 30
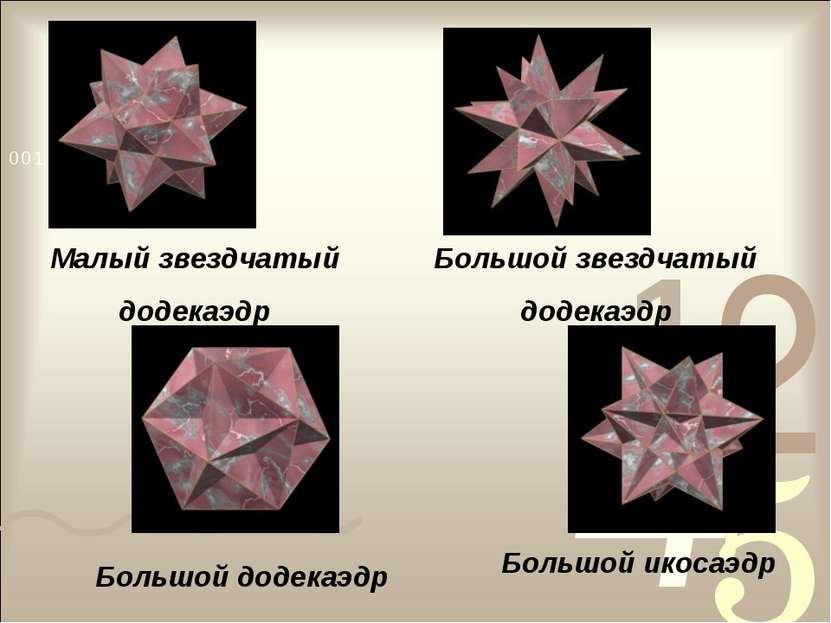
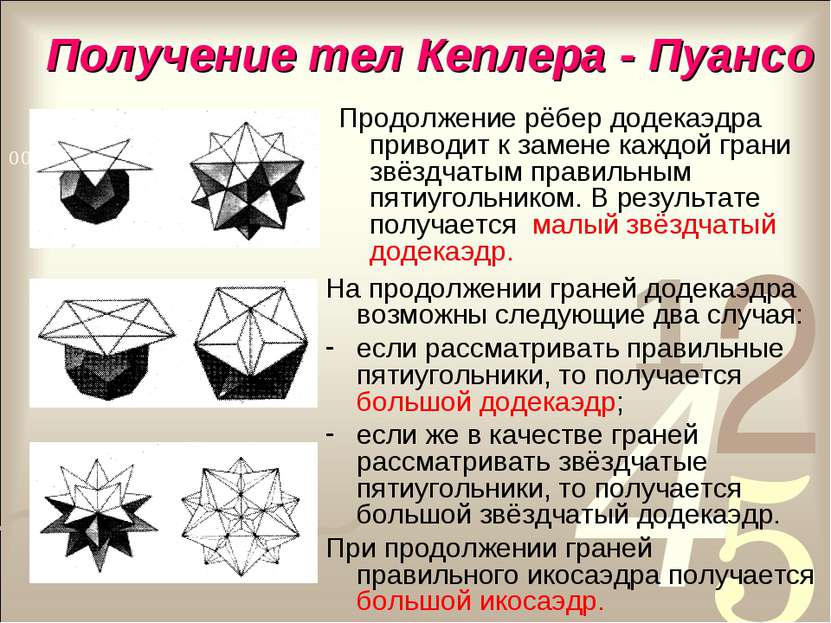
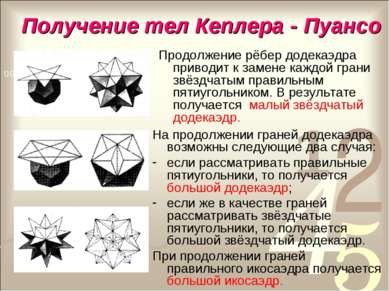Получение тел Кеплера - Пуансо Продолжение рёбер додекаэдра приводит к замене каждой грани звёздчатым правильным пятиугольником. В результате получается малый звёздчатый додекаэдр. На продолжении граней додекаэдра возможны следующие два случая: если рассматривать правильные пятиугольники, то получается большой додекаэдр; если же в качестве граней рассматривать звёздчатые пятиугольники, то получается большой звёздчатый додекаэдр. При продолжении граней правильного икосаэдра получается большой икосаэдр.
Cлайд 31
Иоганн Кеплер (1571-1630)
Cлайд 32
Снежинки – звёздчатые многогранники А вы видели тени от снежинок? А вы знаете, как они танцуют В лунном блеске голубом и чистом Или просто в свете фонаря?
Cлайд 33
Многогранники в геологии Икосаэдро- додекаэдрическая структура Земли.
Cлайд 34
Многогранники в ювелирном деле
Cлайд 35
Многогранники в архитектуре
