X
Код презентации скопируйте его
Объем наклонной призмы, пирамиды и конуса
Скачать эту презентацию
Презентация на тему Объем наклонной призмы, пирамиды и конуса
Скачать эту презентациюCлайд 1
Объем наклонной призмы, пирамиды и конуса.
Cлайд 2
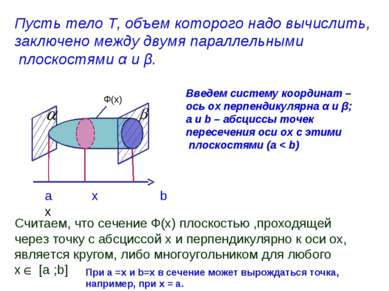Пусть тело Т, объем которого надо вычислить, заключено между двумя параллельными плоскостями α и β. Введем систему координат – ось ох перпендикулярна α и β; а и b – абсциссы точек пересечения оси ох с этими плоскостями (а < b) a x b x Ф(x) Считаем, что сечение Ф(х) плоскостью ,проходящей через точку с абсциссой х и перпендикулярно к оси ох, является кругом, либо многоугольником для любого х [a ;b] При а =х и b=x в сечение может вырождаться точка, например, при х = а.
Cлайд 3
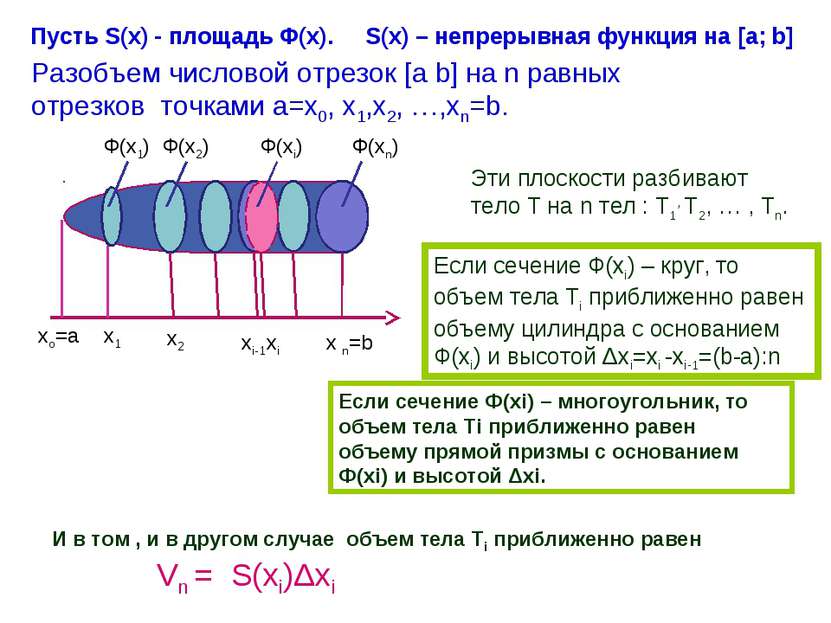
Ф(х1) Ф(х2) Ф(хi) Ф(хn) хо=а х1 х2 хi-1 хi x n=b Пусть S(x) - площадь Ф(х). S(x) – непрерывная функция на [a; b] Разобъем числовой отрезок [a b] на n равных отрезков точками а=х0, х1,х2, …,хn=b. Эти плоскости разбивают тело Т на n тел : Т1, Т2, … , Тn. Если сечение Ф(хi) – круг, то объем тела Тi приближенно равен объему цилиндра с основанием Ф(хi) и высотой Δхi=хi -xi-1=(b-a):n Если сечение Ф(хi) – многоугольник, то объем тела Тi приближенно равен объему прямой призмы с основанием Ф(хi) и высотой Δхi. И в том , и в другом случае объем тела Тi приближенно равен Vn = S(xi)Δxi
Cлайд 4
И в том , и в другом случае объем тела Тi приближенно равен Vn = S(xi)Δxi Основная формула для вычисления объемов.
Cлайд 5
В классе: № 673, № 674 № 674
Cлайд 6
Дано: АВСА1В1С1 - прямая призма.
Cлайд 7
2) Дано: АВСДА1В1С1Д1 – прямая призма, АВСД - ромб, АД=12,
Cлайд 8
3) Дано: АВСДА1В1С1Д1 – прямая призма, АВСД – ромб, АД = 10, ВК ┴ АД, ВК = 5, В1К = 13 Найти: V 13 А В С Д А1 В1 С1 Д1
Cлайд 9
П 67 № 675 Дома:
