X
Код презентации скопируйте его
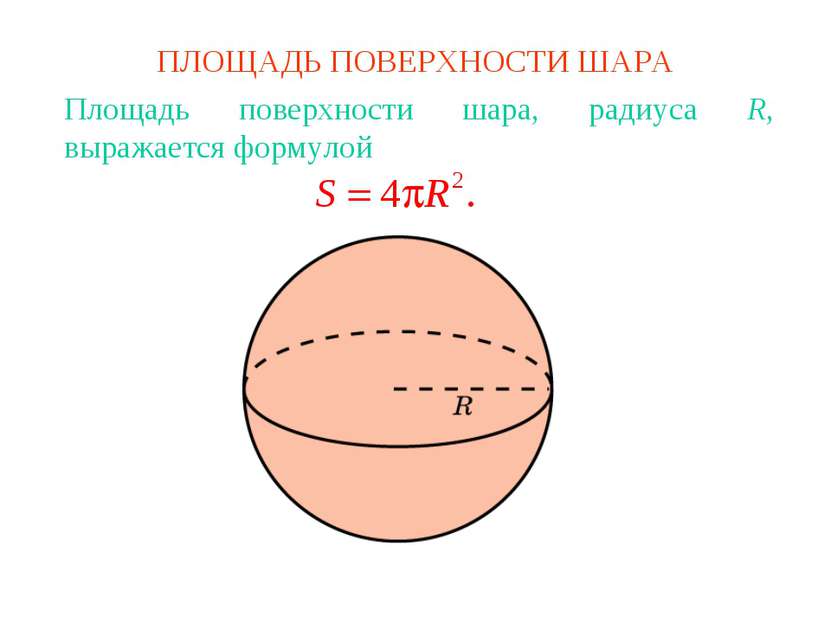
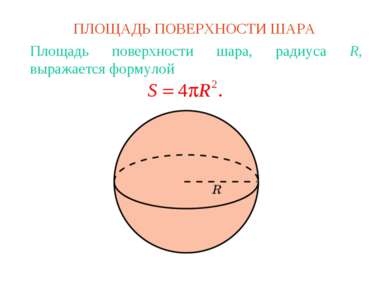
Площадь поверхности шара
Скачать эту презентацию
Презентация на тему Площадь поверхности шара
Скачать эту презентациюCлайд 1
ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРА Площадь поверхности шара, радиуса R, выражается формулой
Cлайд 2
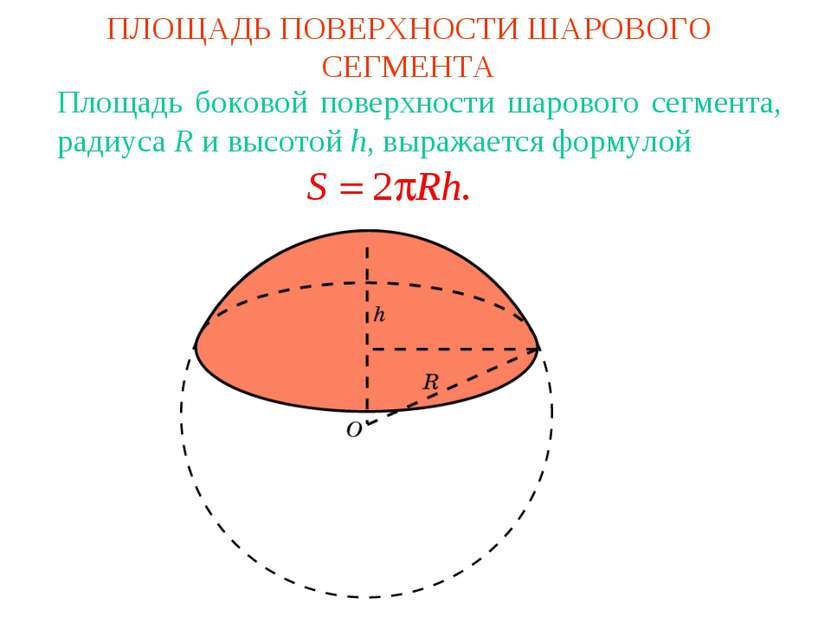
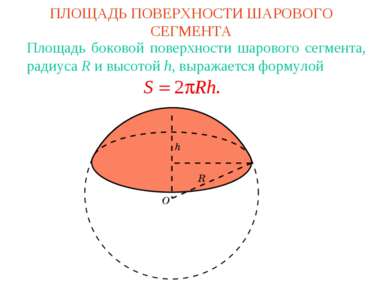ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО СЕГМЕНТА Площадь боковой поверхности шарового сегмента, радиуса R и высотой h, выражается формулой
Cлайд 3
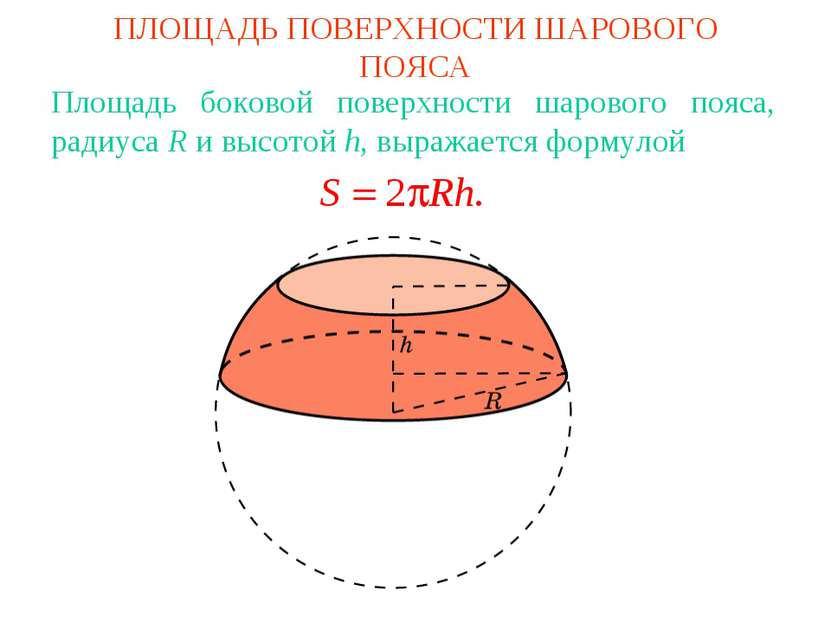
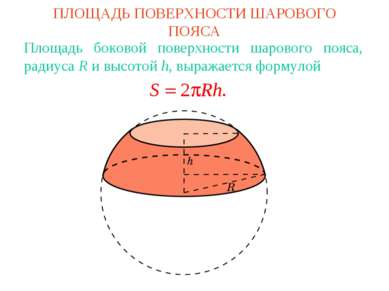ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО ПОЯСА Площадь боковой поверхности шарового пояса, радиуса R и высотой h, выражается формулой
Cлайд 4
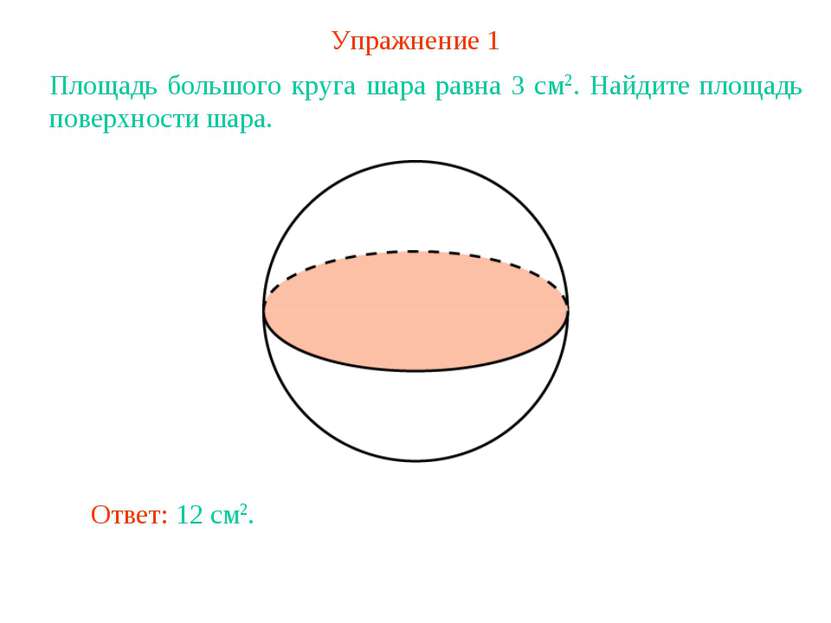
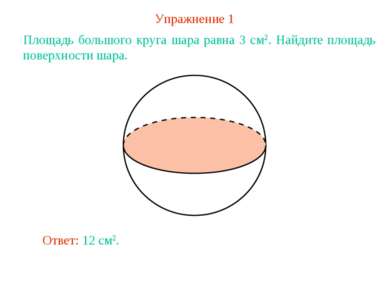Упражнение 1 Площадь большого круга шара равна 3 см2. Найдите площадь поверхности шара. Ответ: 12 см2.
Cлайд 5
Упражнение 2 Как изменится площадь поверхности шара, если увеличить радиус шара в: а) 2 раза; б) 3 раза; в) n раз? Ответ: Увеличится в: а) 4 раза; б) 9 раз; в) n2 раз.
Cлайд 6
Упражнение 3 Площади поверхностей двух шаров относятся как 4 : 9. Найдите отношение их диаметров. Ответ: 2:3.
Cлайд 7
Упражнение 4 Объём шара равен 288 дм3. Найдите площадь его поверхности. Ответ: 144 дм2.
Cлайд 8
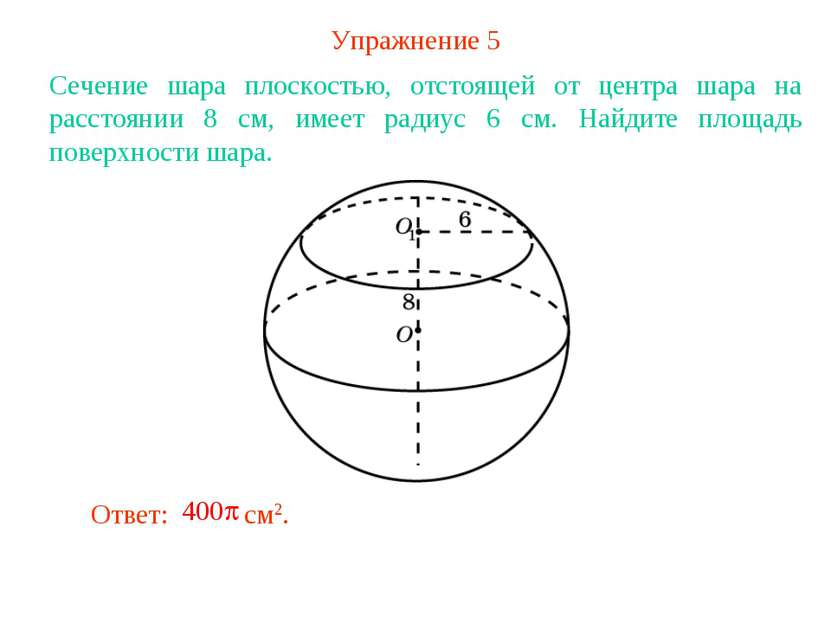
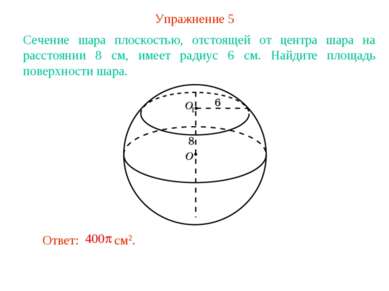Упражнение 5 Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите площадь поверхности шара.
Cлайд 9
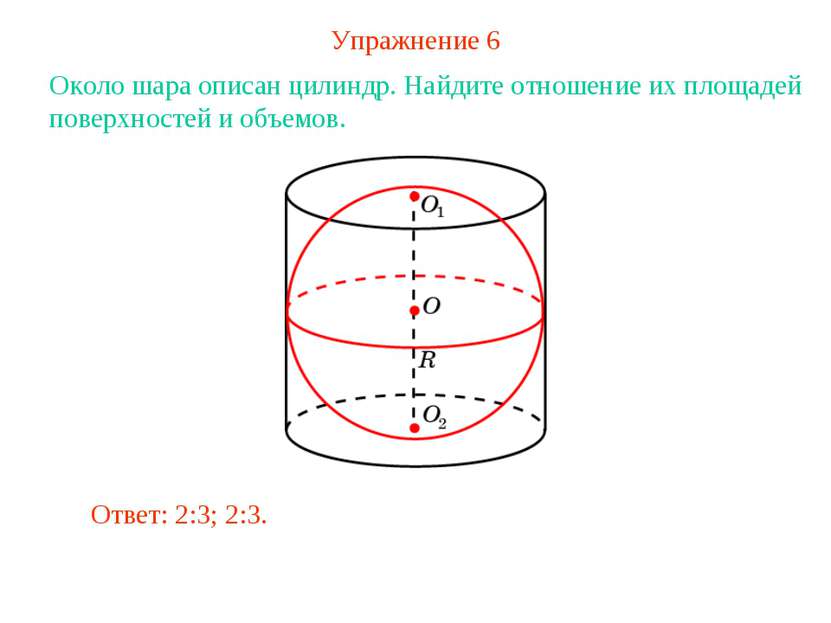
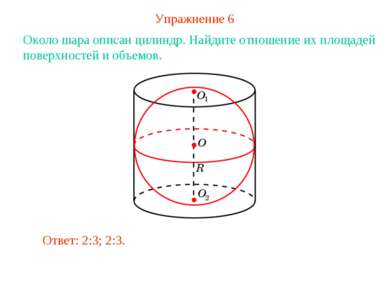Упражнение 6 Около шара описан цилиндр. Найдите отношение их площадей поверхностей и объемов. Ответ: 2:3; 2:3.
Cлайд 10
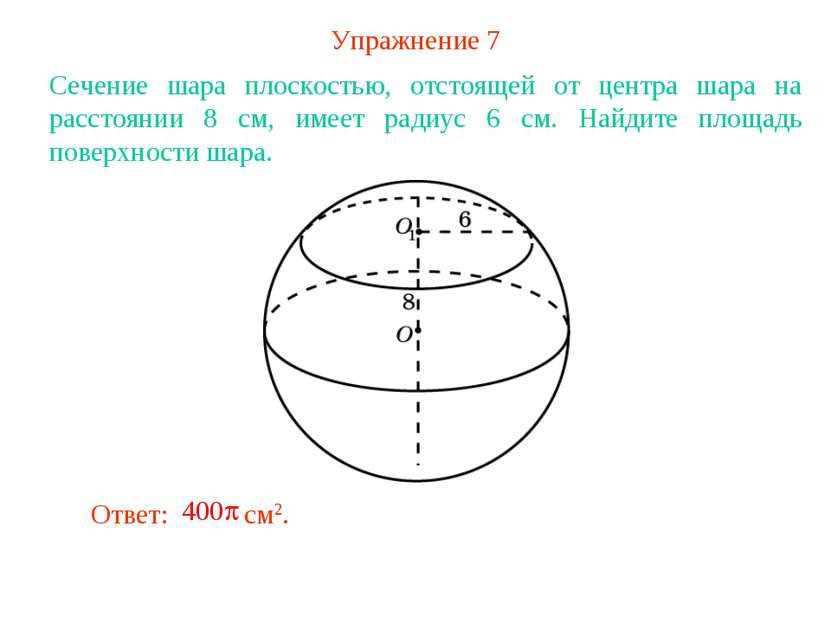
Упражнение 7 Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите площадь поверхности шара.
Cлайд 11
Упражнение 8 Во сколько раз площадь поверхности шара, описанного около куба, больше площади поверхности шара, вписанного в этот же куб? Ответ: В три раза.
Cлайд 12
Упражнение 9 Около прямоугольного параллелепипеда, измерения которого равны 1 дм, 2 дм и 3 дм, описан шар. Найдите площадь его поверхности. Ответ: 14 дм2.
Cлайд 13
Упражнение 10 Около октаэдра, ребро которого равно 2 дм, описан шар. Найдите площадь поверхности шара. Ответ: 8 дм2.
Cлайд 14
Упражнение 11 Около шара описан цилиндр. Найдите отношение их площадей поверхностей и объемов. Ответ: 2 : 3, 2 : 3.
Cлайд 15
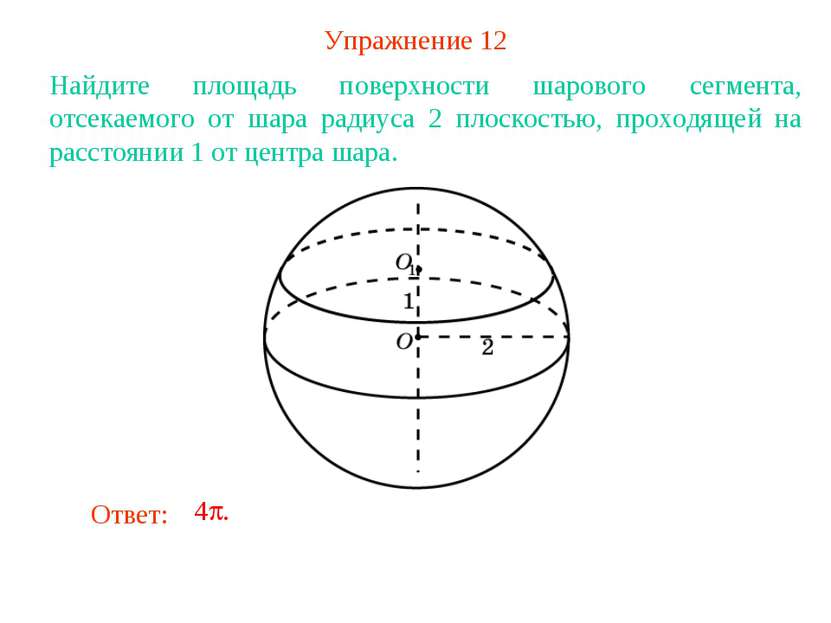
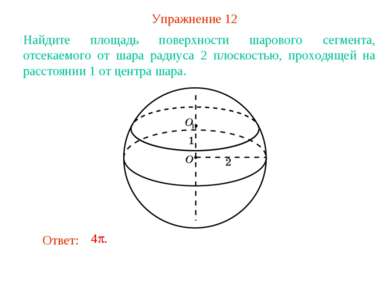Упражнение 12 Найдите площадь поверхности шарового сегмента, отсекаемого от шара радиуса 2 плоскостью, проходящей на расстоянии 1 от центра шара.
Cлайд 16
Упражнение 13 Шар радиуса 1 пересечен двумя параллельными плоскостями, которые делят перпендикулярный им диаметр шара в отношении 1 : 2 : 3. Определите площадь поверхности шара, заключенную между секущими плоскостями.
Cлайд 17
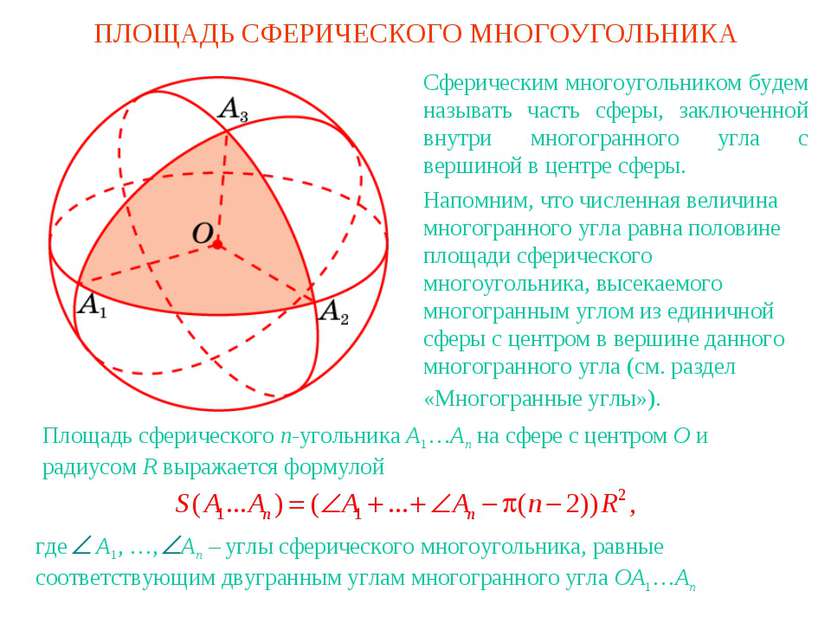
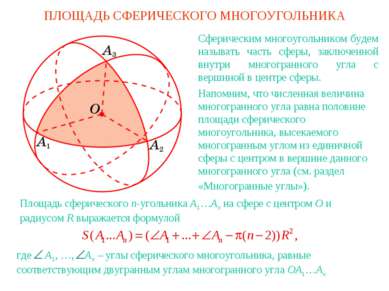ПЛОЩАДЬ СФЕРИЧЕСКОГО МНОГОУГОЛЬНИКА Сферическим многоугольником будем называть часть сферы, заключенной внутри многогранного угла с вершиной в центре сферы. Напомним, что численная величина многогранного угла равна половине площади сферического многоугольника, высекаемого многогранным углом из единичной сферы с центром в вершине данного многогранного угла (см. раздел «Многогранные углы»). где A1, …, An – углы сферического многоугольника, равные соответствующим двугранным углам многогранного угла OA1…An Площадь сферического n-угольника A1…An на сфере с центром O и радиусом R выражается формулой
Cлайд 18
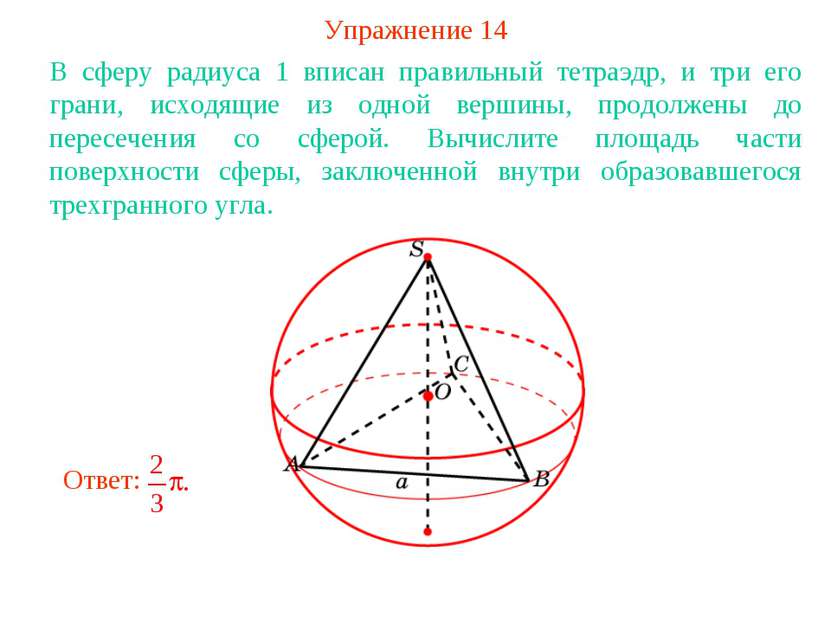
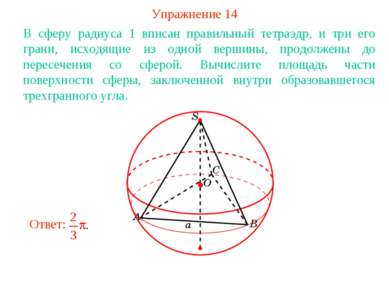Упражнение 14 В сферу радиуса 1 вписан правильный тетраэдр, и три его грани, исходящие из одной вершины, продолжены до пересечения со сферой. Вычислите площадь части поверхности сферы, заключенной внутри образовавшегося трехгранного угла.
Cлайд 19
Упражнение 15 Найдите площадь сферического треугольника на единичной сфере, углы которого равны: а) 90о; б) 90о; в) 90о. Решение. Данный треугольник составляет одну восьмую часть единичной сферы.
Cлайд 20
Упражнение 16 Найдите площадь сферического треугольника на единичной сфере, углы которого равны: а) 80о; б) 90о; в) 100о.
Cлайд 21
Упражнение 17 Центром единичной сферы является вершина правильной четырехугольной пирамиды с ребром основания 2 и высотой 1. Найдите площадь части сферы, заключенной внутри пирамиды.
Cлайд 22
Упражнение 18 Найдите площадь сферического треугольника, образованного трехгранным углом единичного тетраэдра ABCD и единичной сферой с центром в вершине D тетраэдра.
Cлайд 23
Упражнение 19 Найдите площадь сферического четырехугольника, образованного четырехгранным углом единичного октаэдра SABCDS’ и единичной сферой с центром в вершине S октаэдра.
Cлайд 24
Упражнение 20 Найдите площадь сферического пятиугольника, образованного пятигранным углом единичного икосаэдра и единичной сферой с центром в вершине икосаэдра.
Cлайд 25
Упражнение 21 Найдите площадь сферического треугольника, образованного трехгранным углом единичного додекаэдра и единичной сферой с центром в вершине додекаэдра.
