X
Код презентации скопируйте его
Масштаб. Длина окружности и площадь круга
Скачать эту презентацию
Презентация на тему Масштаб. Длина окружности и площадь круга
Скачать эту презентациюCлайд 1
Цель урока: 1) закрепить понятия масштаба, длины окружности и площади круга. 2) совершенствовать умения находить расстояние на карте и на местности, зная масштаб, площадь круга и длину окружности. 3) Активизировать познавательную деятельность учащихся. 4) показать применение знаний на практике, расширить кругозор учащихся при решении практических задач;
Cлайд 2
Организационный момент. Устные упражнения. Работа по карточкам. Работа с самопроверкой. Задачи практического содержания. Самостоятельная дифференцированная работа с обучающей компьютерной программой. Занимательная страничка. Домашнее задание. Подведение итогов урока.
Cлайд 3
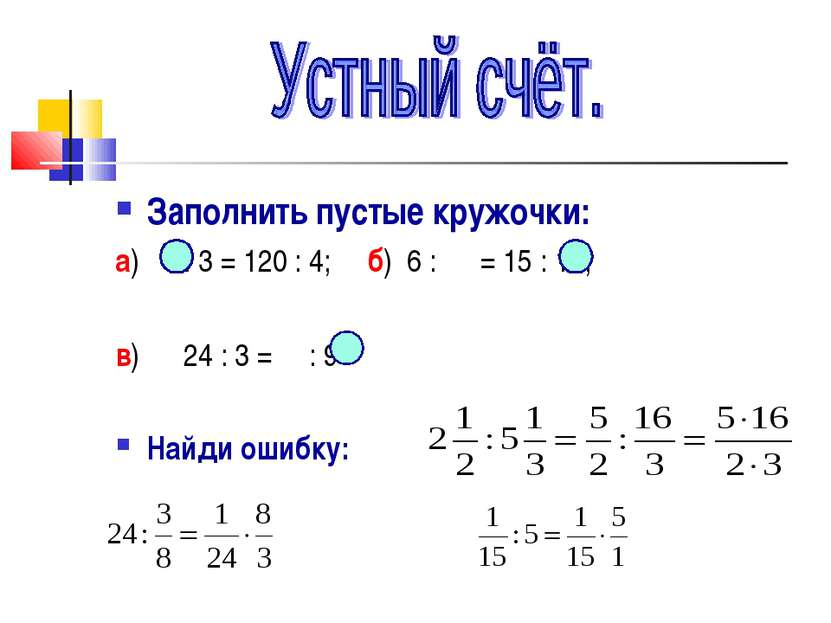
Заполнить пустые кружочки: а) : 3 = 120 : 4; б) 6 : = 15 : 10; в) 24 : 3 = : 9 Найди ошибку:
Cлайд 4
№ Масштаб карты Расстояние на карте на местности 1 а) 1:10000 ? 5 км 2 б) 1:25000 36 мм ? 3 в) 1:50000 ? 12 км 4 г) 1:100000 15 см ? 5 д) 1:2000000 ? 40 км 6 ж) 1:25000 3,6 см ? 7 е) 1:50000 4 см ?
Cлайд 5
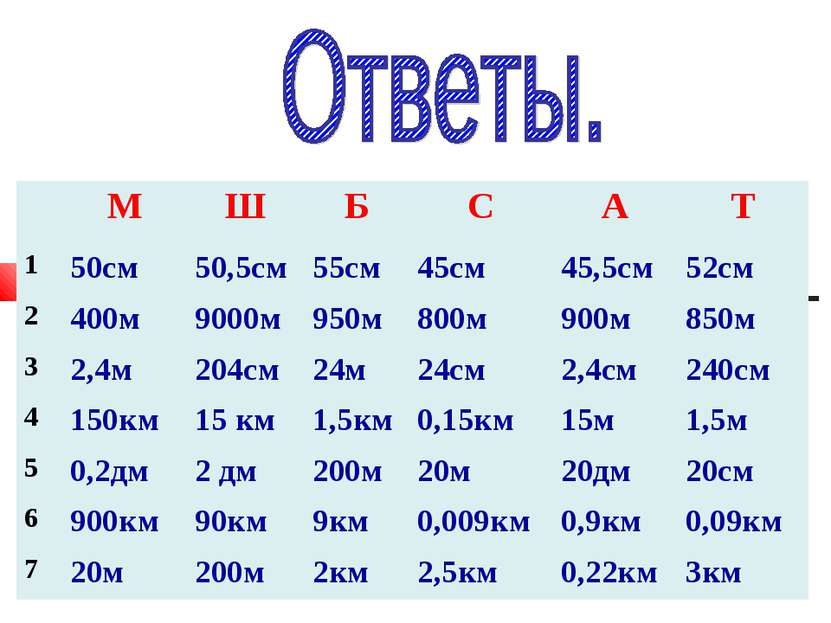
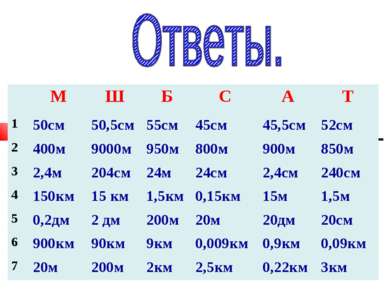М Ш Б С А Т 1 50см 50,5см 55см 45см 45,5см 52см 2 400м 9000м 950м 800м 900м 850м 3 2,4м 204см 24м 24см 2,4см 240см 4 150км 15 км 1,5км 0,15км 15м 1,5м 5 0,2дм 2 дм 200м 20м 20дм 20см 6 900км 90км 9км 0,009км 0,9км 0,09км 7 20м 200м 2км 2,5км 0,22км 3км
Cлайд 6
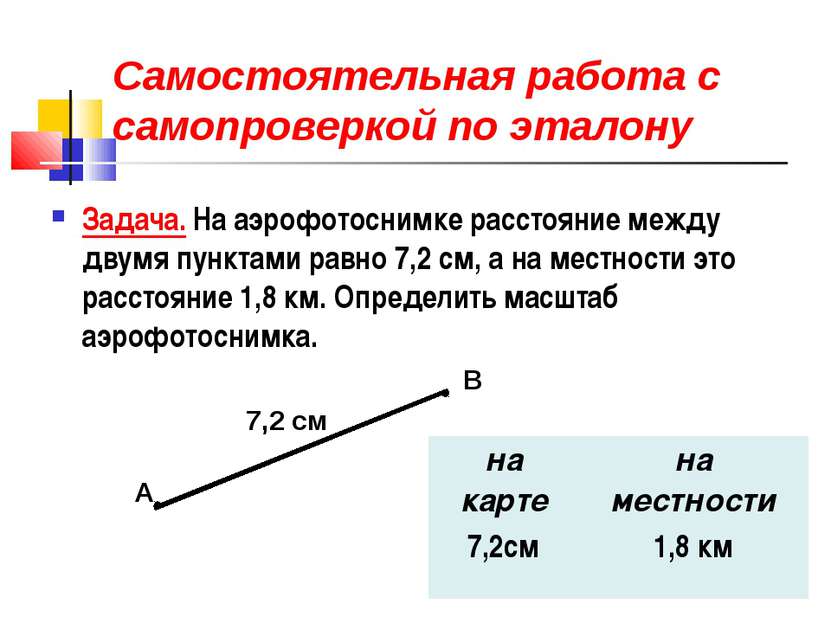
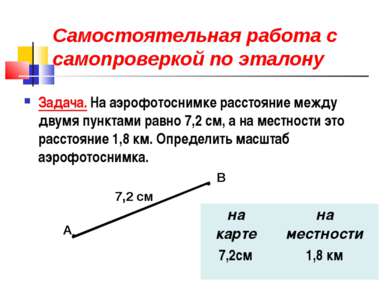
Самостоятельная работа с самопроверкой по эталону Задача. На аэрофотоснимке расстояние между двумя пунктами равно 7,2 см, а на местности это расстояние 1,8 км. Определить масштаб аэрофотоснимка. А В 7,2 см на карте на местности 7,2см 1,8 км
Cлайд 7
Решение. 1,8 км = 1 800 м = 180 000 см Ответ: 1: 25 000
Cлайд 8
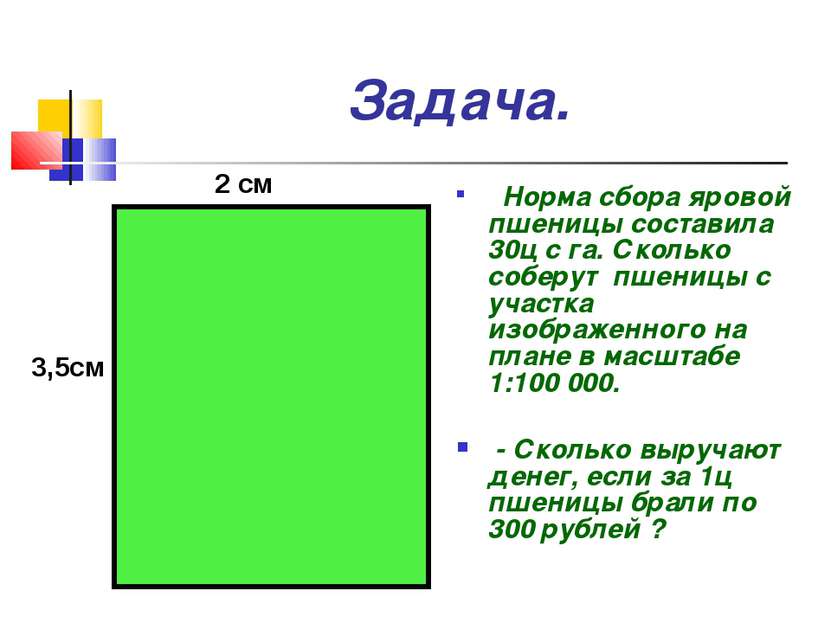
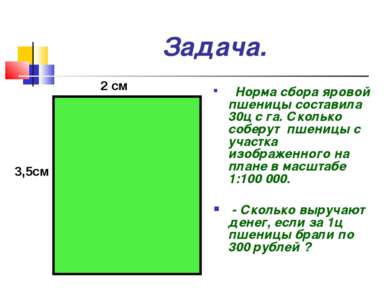
Задача. Норма сбора яровой пшеницы составила 30ц с га. Сколько соберут пшеницы с участка изображенного на плане в масштабе 1:100 000. - Сколько выручают денег, если за 1ц пшеницы брали по 300 рублей ? 2 см 3,5см
Cлайд 9
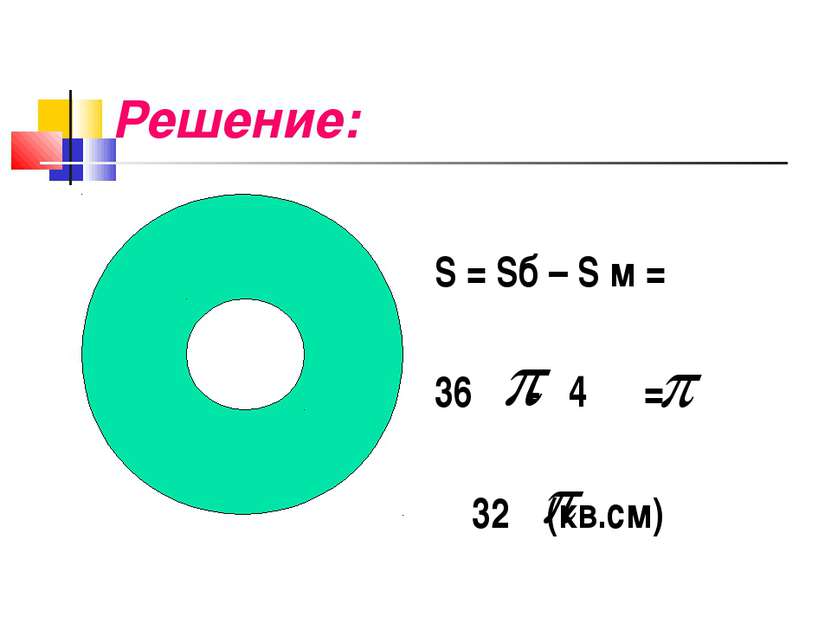
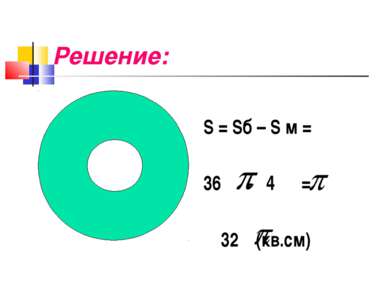
Компьютерная задачка. (Решение в группах) Найдите площадь поверхности компьютерного диска. Радиус большого круга равен 6 см, а радиус малого круга – 2 см.
Cлайд 10
Решение: S = Sб – S м = 36 - 4 = 32 (кв.см)
Cлайд 11
Работа по учебнику Выполняем упр. № 838; № 839; № 863.
Cлайд 12
диск УЭИ «Математика 5-11» Задачи-исследования на тему «Золотое сечение» № 10 а), б) (для подготовленных учащихся) (раздел «Деление в данном отношении») Задача № 10а (работа в группе) ( раздел «Что такое отношение?»)
Cлайд 13
Еще древние греки проводили много экспериментов, и установили, что отношение C к d (длины окружности к диаметру) равно бесконечной дроби 3,1415926… Это число было настолько великим, что греки его стали воспринимать как магическое число и назвали его в честь великого древнегреческого ученого ПИФАГОРА – ПИ. Есть специальная считалочка, с помощью которой можно запомнить семь знаков после запятой в числе ПИ. «Нужно только постараться и запомнить все, как есть: «Три – четырнадцать – пятнадцать-девяносто два и шесть.»
Cлайд 14
Верёвочкой очерчен круг. Я возьму сейчас эту веревку и очерчу ею два круга, равных между собой. Как видите, длина веревки не изменилась. Скажите, а площадь исходного круга равна сумме площадей этих двух кругов?
Cлайд 15
Составить задачу практического содержания по теме: «Длина окружности. Площадь круга». Выполнить № 866; № 872. Подготовиться к контрольной работе.
