X
Код презентации скопируйте его
Решение задач на применение аксиом стереометрии и их следствий
Скачать эту презентацию
Презентация на тему Решение задач на применение аксиом стереометрии и их следствий
Скачать эту презентациюCлайд 1
Урок 3.
Cлайд 2
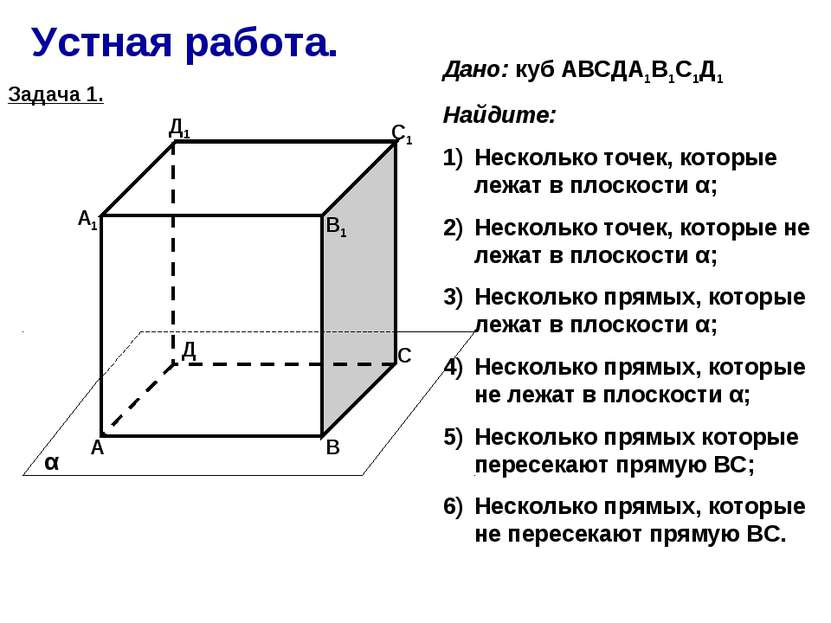
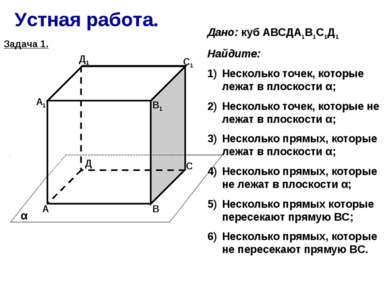Устная работа. А В С Д А1 В1 С1 Д1 α Дано: куб АВСДА1В1С1Д1 Найдите: Несколько точек, которые лежат в плоскости α; Несколько точек, которые не лежат в плоскости α; Несколько прямых, которые лежат в плоскости α; Несколько прямых, которые не лежат в плоскости α; Несколько прямых которые пересекают прямую ВС; Несколько прямых, которые не пересекают прямую ВС. Задача 1.
Cлайд 3
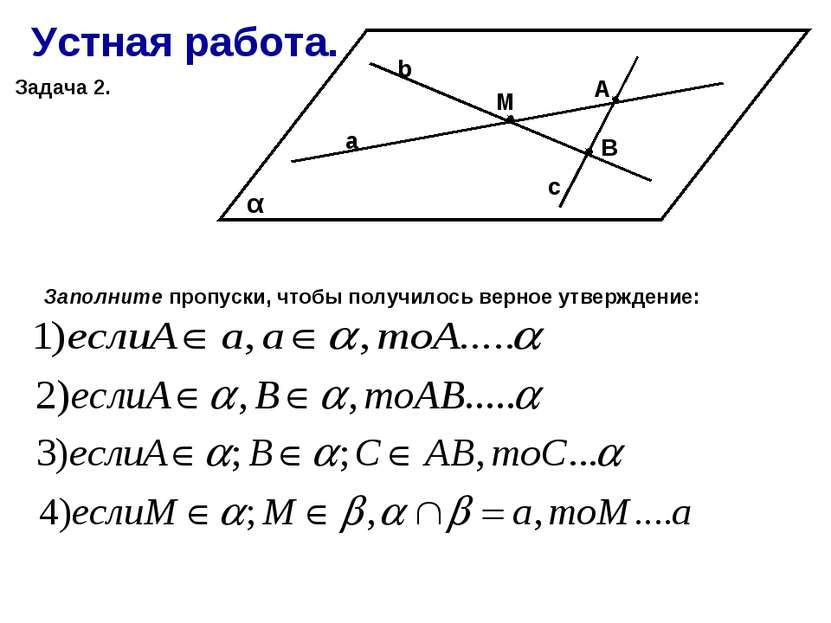
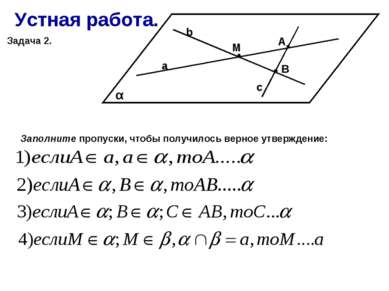Устная работа. Задача 2. α А М В а b c Заполните пропуски, чтобы получилось верное утверждение:
Cлайд 4
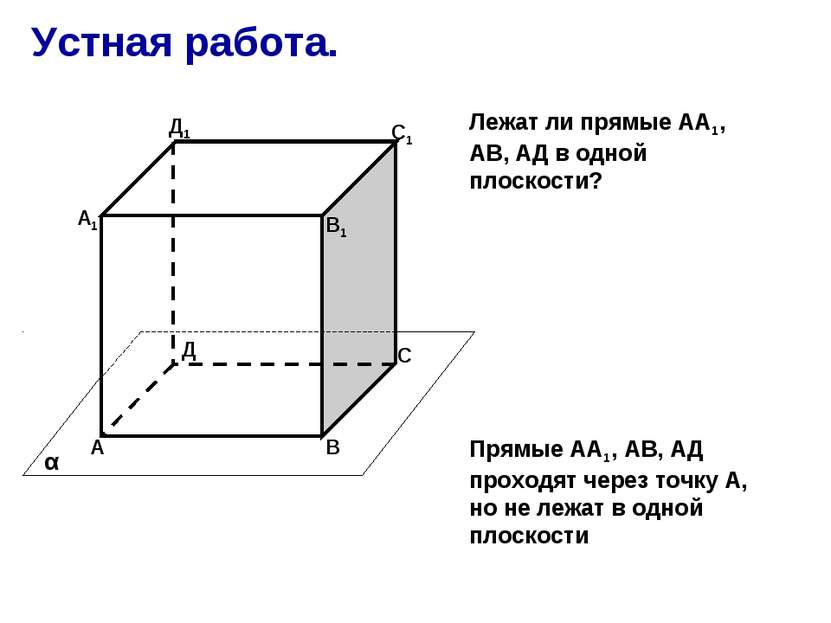
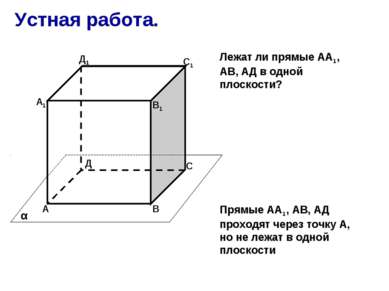Устная работа. А В С Д А1 В1 С1 Д1 α Прямые АА1, АВ, АД проходят через точку А, но не лежат в одной плоскости Лежат ли прямые АА1, АВ, АД в одной плоскости?
Cлайд 5
Решите задачи из учебного пособия: стр. 8 № 7, 10, 14. Работа учащихся на доске и в тетрадях:
Cлайд 6
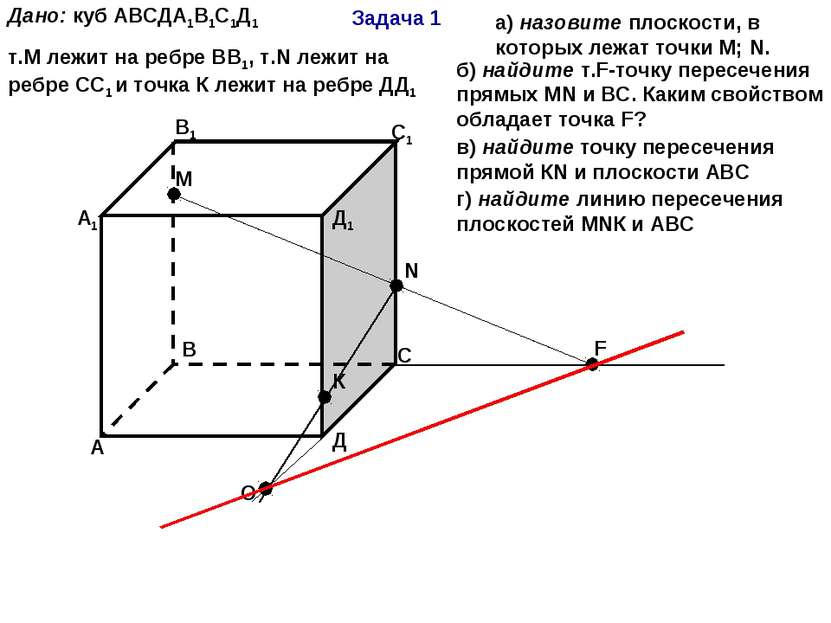
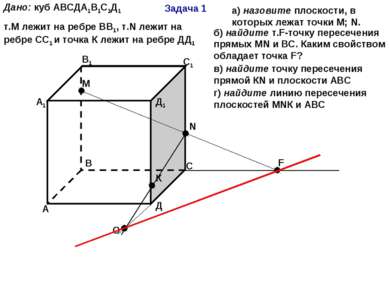Задача 1 А В С Д А1 В1 С1 Д1 М N F К Дано: куб АВСДА1В1С1Д1 т.М лежит на ребре ВВ1, т.N лежит на ребре СС1 и точка К лежит на ребре ДД1 а) назовите плоскости, в которых лежат точки М; N. б) найдите т.F-точку пересечения прямых МN и ВС. Каким свойством обладает точка F? в) найдите точку пересечения прямой КN и плоскости АВС О г) найдите линию пересечения плоскостей МNК и АВС
Cлайд 7
А В С Д О Повторение. Формула для вычисления площади четырехугольника.
Cлайд 8
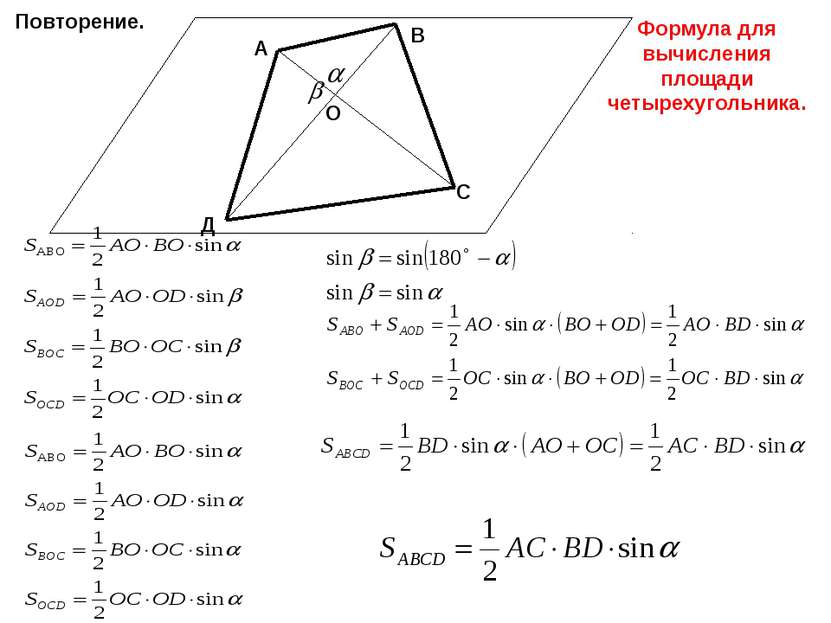
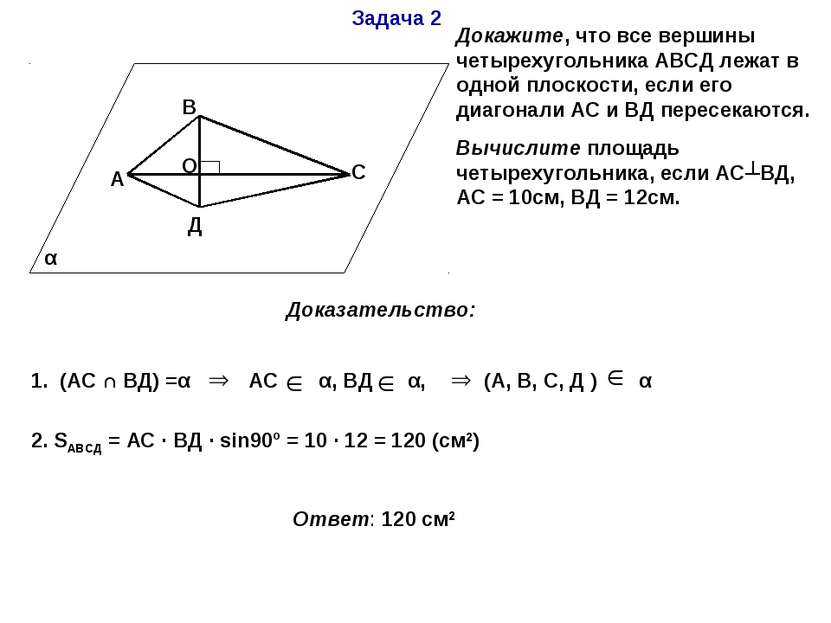
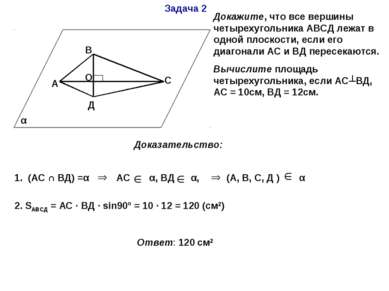Задача 2 α А В С Д О Докажите, что все вершины четырехугольника АВСД лежат в одной плоскости, если его диагонали АС и ВД пересекаются. Вычислите площадь четырехугольника, если АС┴ВД, АС = 10см, ВД = 12см. Доказательство: 1. (АС ∩ ВД) =α АС α, ВД α, (А, В, С, Д ) α 2. SАВСД = АС · ВД · sin90º = 10 · 12 = 120 (см2) Ответ: 120 см2
Cлайд 9
Домашнее задание: Пункты 1-3 прочитать Решить задачи № 9; 13 Дополнительно № 11; 15 ( по желанию)
