X
Код презентации скопируйте его
Сфера и шар 9 класс
Скачать эту презентацию
Презентация на тему Сфера и шар 9 класс
Скачать эту презентациюCлайд 1
Сфера и шар учитель математики МБОУ Одинцовской гимназии №13 Владимирова Л.М. 11 класс
Cлайд 2
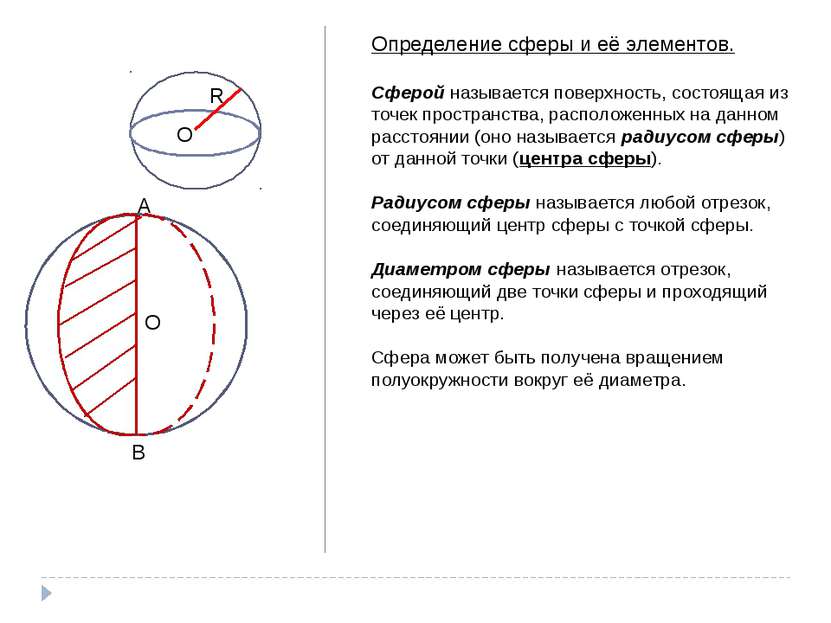
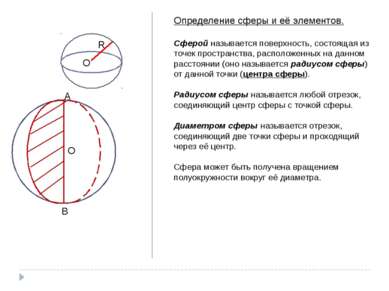R O Определение сферы и её элементов. Сферой называется поверхность, состоящая из точек пространства, расположенных на данном расстоянии (оно называется радиусом сферы) от данной точки (центра сферы). Радиусом сферы называется любой отрезок, соединяющий центр сферы с точкой сферы. Диаметром сферы называется отрезок, соединяющий две точки сферы и проходящий через её центр. Сфера может быть получена вращением полуокружности вокруг её диаметра. A B O
Cлайд 3
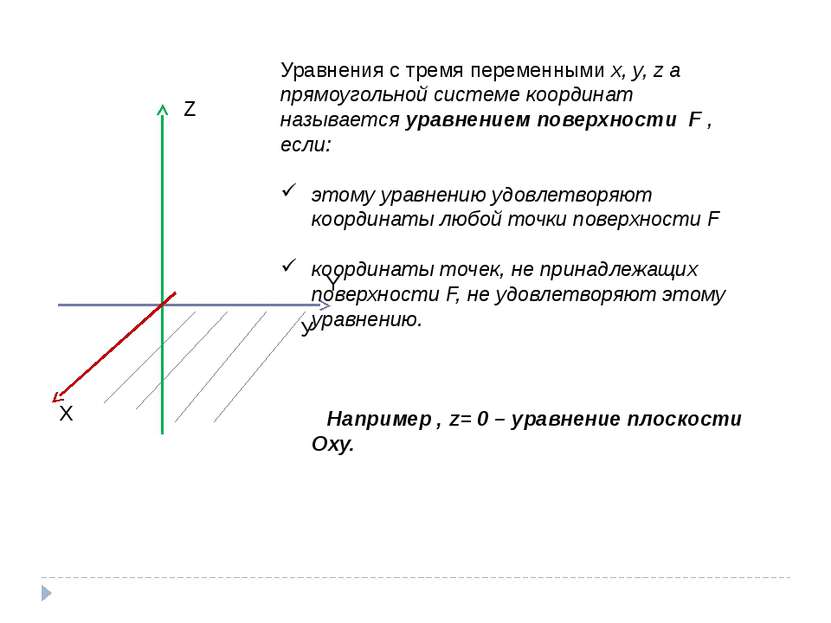
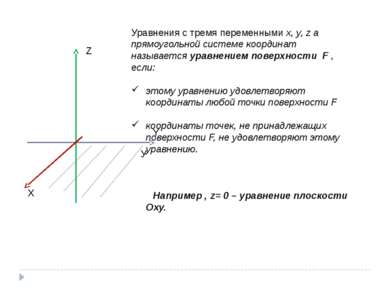Z Y X Уравнения с тремя переменными x, y, z а прямоугольной системе координат называется уравнением поверхности F , если: этому уравнению удовлетворяют координаты любой точки поверхности F координаты точек, не принадлежащих поверхности F, не удовлетворяют этому уравнению. Например , z= 0 – уравнение плоскости Оху. У
Cлайд 4
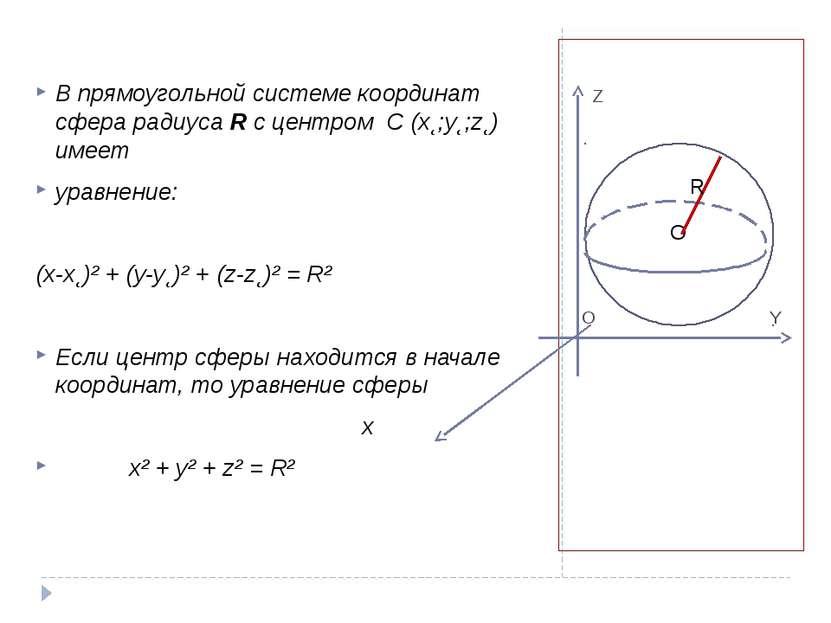
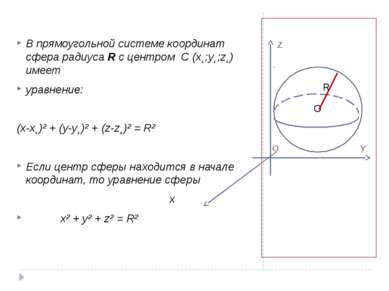Z O Y В прямоугольной системе координат сфера радиуса R с центром C (x˛;y˛;z˛) имеет уравнение: (x-x˛)² + (y-y˛)² + (z-z˛)² = R² Если центр сферы находится в начале координат, то уравнение сферы x x² + y² + z² = R² O R
Cлайд 5
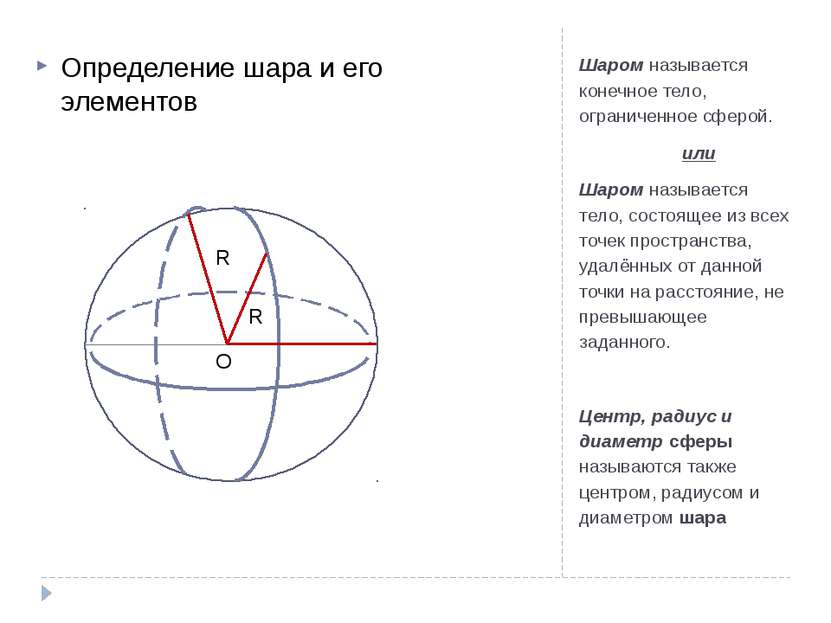
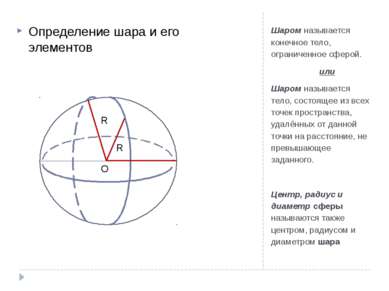Шаром называется конечное тело, ограниченное сферой. или Шаром называется тело, состоящее из всех точек пространства, удалённых от данной точки на расстояние, не превышающее заданного. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара Определение шара и его элементов R R О
Cлайд 6
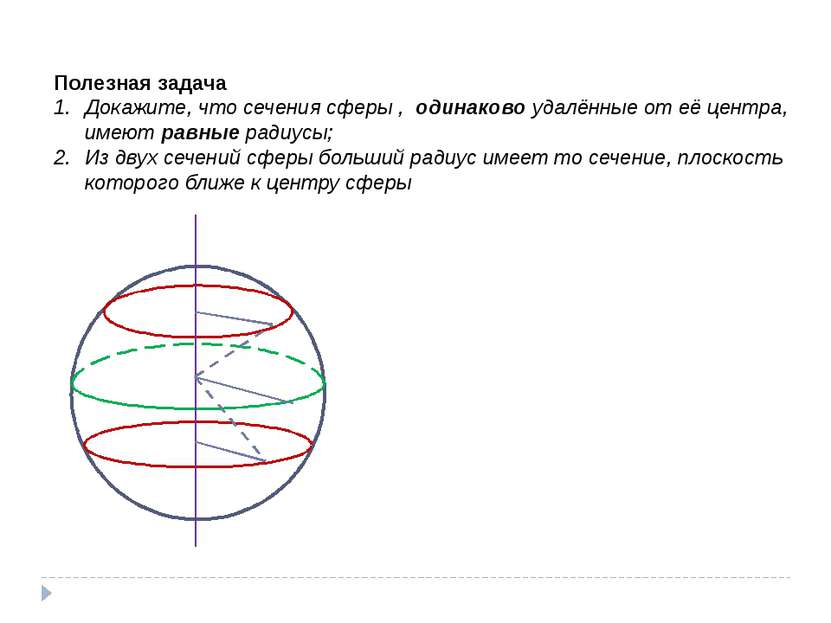
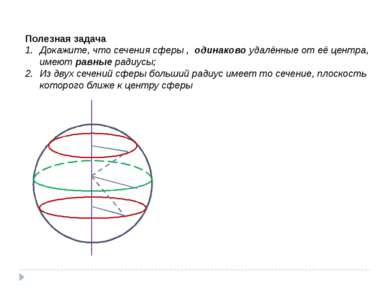Полезная задача Докажите, что сечения сферы , одинаково удалённые от её центра, имеют равные радиусы; Из двух сечений сферы больший радиус имеет то сечение, плоскость которого ближе к центру сферы
Cлайд 7
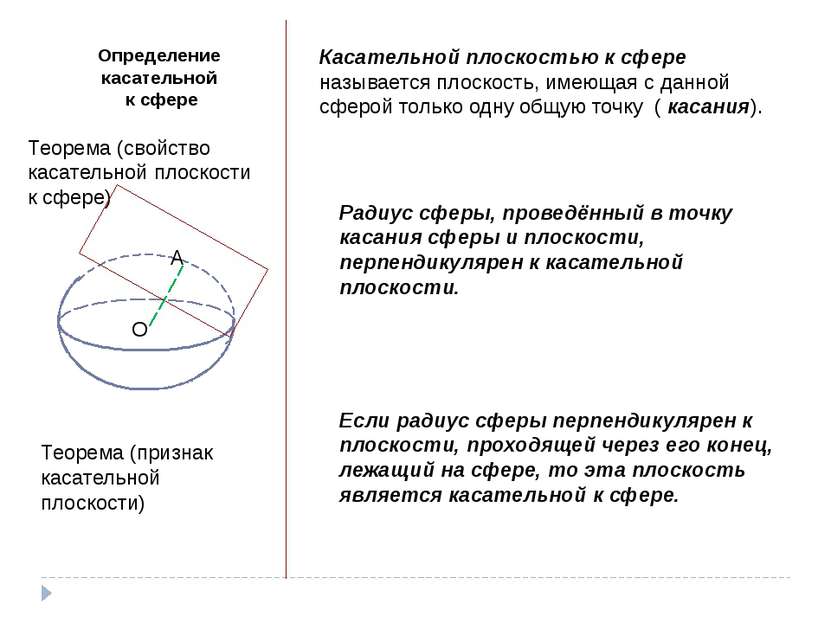
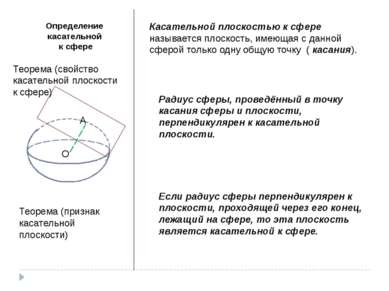Определение касательной к сфере Касательной плоскостью к сфере называется плоскость, имеющая с данной сферой только одну общую точку ( касания). Теорема (свойство касательной плоскости к сфере) О А Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Теорема (признак касательной плоскости) Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Cлайд 8
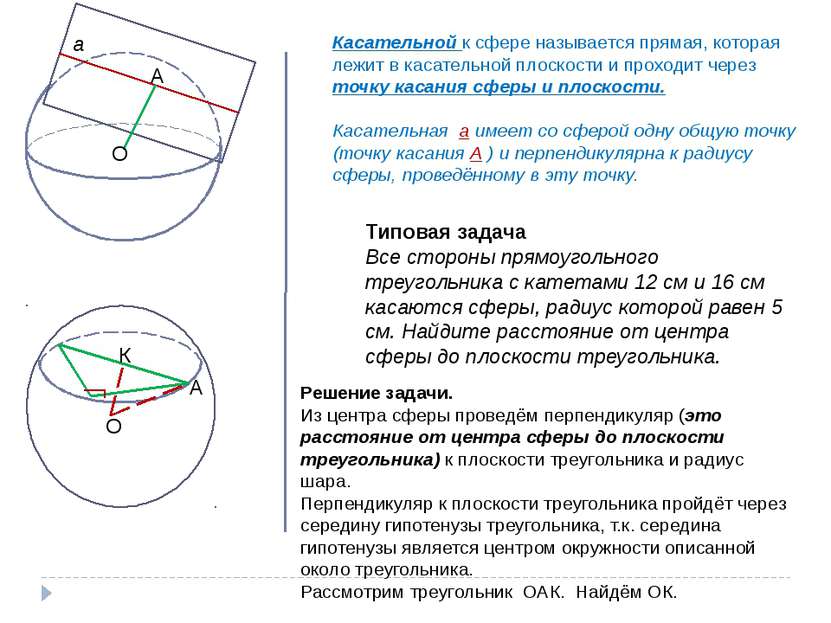
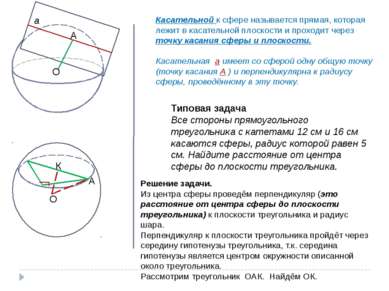О А Касательной к сфере называется прямая, которая лежит в касательной плоскости и проходит через точку касания сферы и плоскости. Касательная а имеет со сферой одну общую точку (точку касания А ) и перпендикулярна к радиусу сферы, проведённому в эту точку. а Типовая задача Все стороны прямоугольного треугольника с катетами 12 см и 16 см касаются сферы, радиус которой равен 5 см. Найдите расстояние от центра сферы до плоскости треугольника. О Решение задачи. Из центра сферы проведём перпендикуляр (это расстояние от центра сферы до плоскости треугольника) к плоскости треугольника и радиус шара. Перпендикуляр к плоскости треугольника пройдёт через середину гипотенузы треугольника, т.к. середина гипотенузы является центром окружности описанной около треугольника. Рассмотрим треугольник ОАК. Найдём ОК. А К
Cлайд 9
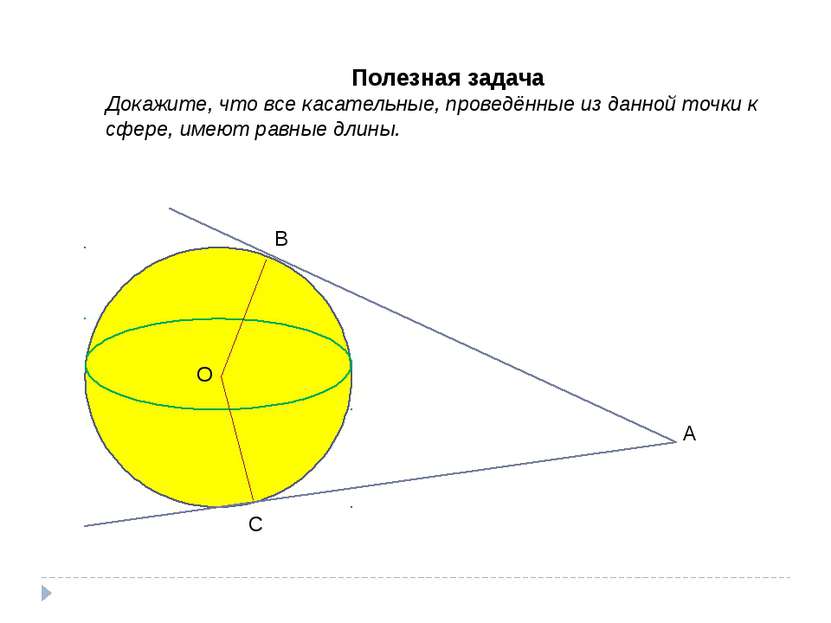
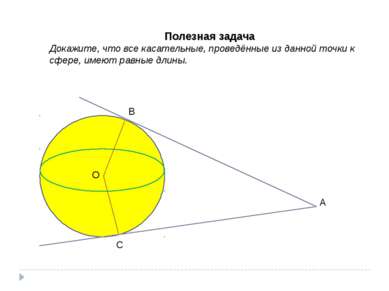Полезная задача Докажите, что все касательные, проведённые из данной точки к сфере, имеют равные длины. О А В С
Cлайд 10
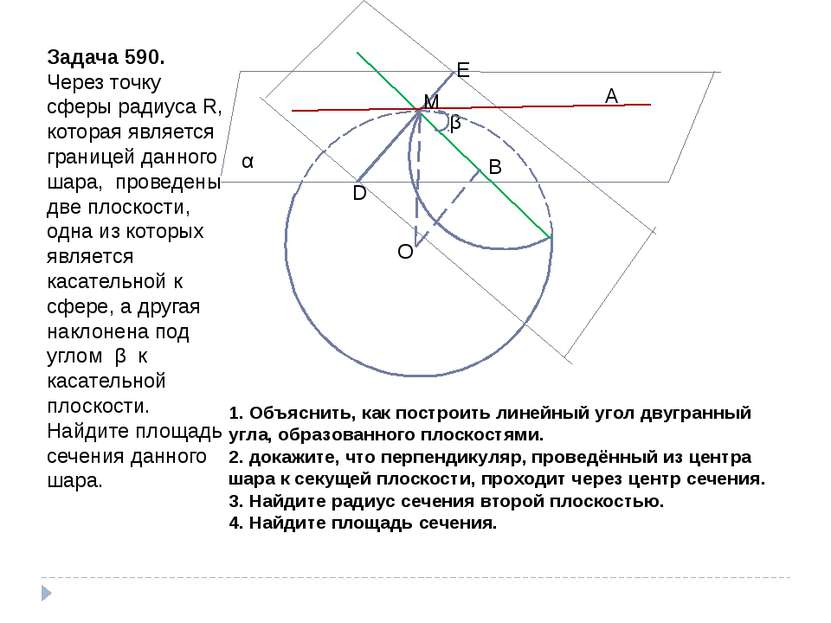
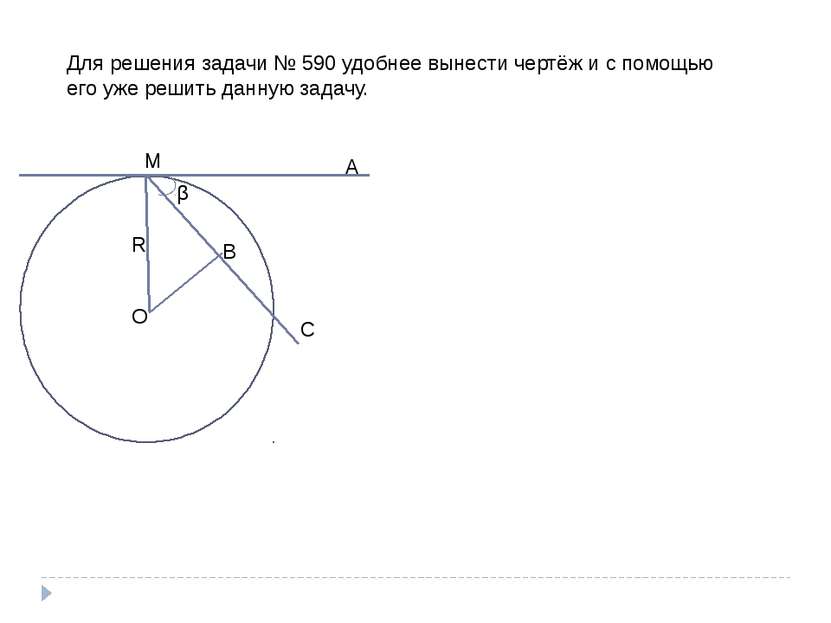
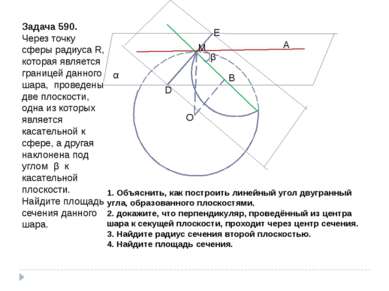Задача 590. Через точку сферы радиуса R, которая является границей данного шара, проведены две плоскости, одна из которых является касательной к сфере, а другая наклонена под углом β к касательной плоскости. Найдите площадь сечения данного шара. β α О М А D E B 1. Объяснить, как построить линейный угол двугранный угла, образованного плоскостями. 2. докажите, что перпендикуляр, проведённый из центра шара к секущей плоскости, проходит через центр сечения. 3. Найдите радиус сечения второй плоскостью. 4. Найдите площадь сечения.
Cлайд 11
Для решения задачи № 590 удобнее вынести чертёж и с помощью его уже решить данную задачу. β О R M A B C
Cлайд 12
Для создания презентации были использованы: учебник по геометрии автор – Атаносян Л.С. «Изучение геометрии в 10-11 классах» (методические рекомендации к учебнику) авторы Л.С. Атанасян и др.
