X
Код презентации скопируйте его
ГИА – 2013 г.Модуль «Алгебра». № 6
Скачать эту презентацию
Презентация на тему ГИА – 2013 г.Модуль «Алгебра». № 6
Скачать эту презентациюCлайд 1
ГИА – 2013 г. Модуль «Алгебра». № 6 Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназии №1 г. Лебедянь Липецкой области
Cлайд 2
ГИА – 2013 г. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. М.: Изд. «Национальное образование», 2013.
Cлайд 3
Арифметическая прогрессия Какая последовательность называется арифметической прогрессией? Какой формулой можно записать арифметическую прогрессию? Как найти разность арифметической прогрессии? Какой формулой выражается n-ый член арифметической прогрессии? Как можно вычислить сумму n первых членов арифметической прогрессии?
Cлайд 4
Повторение *
Cлайд 5
Модуль «Алгебра» Ответ: ⎕⎕⎕⎕
Cлайд 6
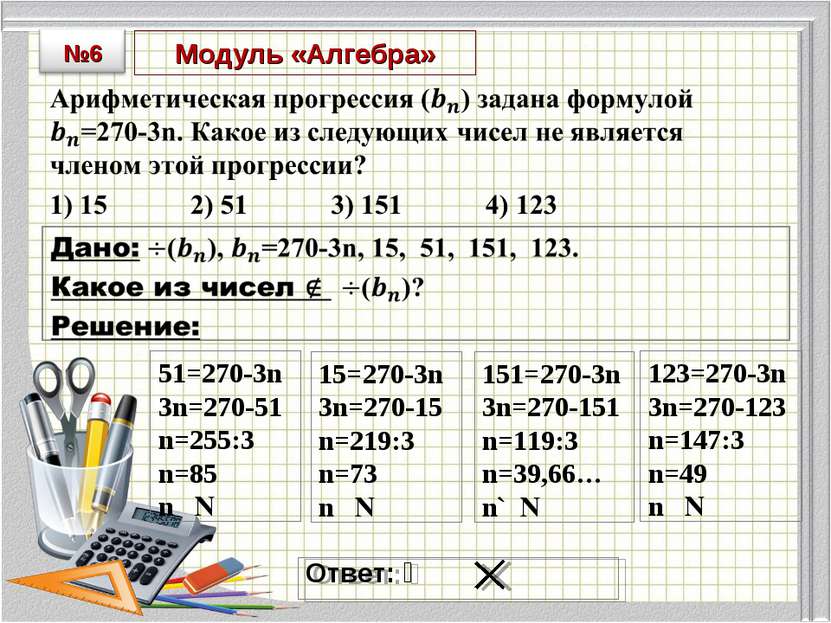
Модуль «Алгебра» Ответ: ⎕ ⎕ ⎕ ⎕ 51=270-3n 3n=270-51 n=255:3 n=85 n∊N 123=270-3n 3n=270-123 n=147:3 n=49 n∊N 151=270-3n 3n=270-151 n=119:3 n=39,66… n∉N 15=270-3n 3n=270-15 n=219:3 n=73 n∊N
Cлайд 7
Модуль «Алгебра» Ответ: 24
Cлайд 8
Модуль «Алгебра» Ответ: 5
Cлайд 9
Модуль «Алгебра» Дана арифметическая прогрессия: -4; -1; 2; … . Найдите сумму первых шести её членов. Ответ: 21
Cлайд 10
Модуль «Алгебра» Ответ: 20
Cлайд 11
Геометрическая прогрессия Какая последовательность называется геометрической прогрессией? Какой формулой можно записать геометрическую прогрессию? Как найти знаменатель геометрической прогрессии? Какой формулой выражается n-ый член геометрической прогрессии? Как можно вычислить сумму n первых членов геометрической прогрессии?
Cлайд 12
Повторение *
Cлайд 13
Модуль «Алгебра» Геометрическая прогрессия (an) задана формулой . Какоe из следующих чисел не является членом прогрессии: 1) 24 2) 72 3) 192 4) 384 ? Дано: (an), Решение: подставим поочередно данные числа в формулу n-го члена прогрессии и найдем n (порядковый номер). Если n – натуральное, то число является членом данной прогрессии. 3∙2ⁿ=24 2ⁿ=8 n=3 N 3∙2ⁿ=72 2ⁿ=24 n N 3∙2ⁿ=384 2ⁿ=138 n=7 N 3∙2ⁿ=192 2ⁿ= 64 n =6 N Ответ: ⎕ ⎕ ⎕ ⎕
Cлайд 14
Модуль «Алгебра» Геометрическая прогрессия (bn) задана условиями b₁= , bn+1=3bn. Найдите b5. Ответ: 40,5 Дано: (bn), b₁= , n=5, bn+1=3bn. Решение:
Cлайд 15
Модуль «Алгебра» (an) - геометрическая прогрессия: b4= -1, b7=27. Найдите знаменатель этой прогрессии. Ответ: -3 Дано: (an), b4= -1, b7=27. Решение: ⇒ ⇒ ⇒
Cлайд 16
Модуль «Алгебра» Дана геометрическая прогрессия: , 1, 4. Найдите произведение первых пяти ее членов. Ответ: 1024. Дано: (bn): , 1, 4. Решение: ⇒
Cлайд 17
Модуль «Алгебра» (bn) – геометрическая прогрессия, знаменатель которой равен 3, b₁= . Найдите сумму первых пяти её членов. Ответ: Дано: (bn), q=3, b₁= , n=5. Решение:
Cлайд 18
«ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов»/ под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013. Автор шаблона: Ранько Елена Алексеевна - учитель начальных классов МАОУ лицей №21 г. Иваново http://www.uchportal.ru/load/160-1-0-31926
