X
Код презентации скопируйте его
Решение показательных неравенств
Скачать эту презентацию
Презентация на тему Решение показательных неравенств
Скачать эту презентациюCлайд 1
Решение показательных неравенств Разработала учитель математики средней школы № 8 города Елабуги Герасимова Л.Н.
Cлайд 2
Структура изучения 1. Решение неравенства 2. Простейшие показательные неравенства 3. Решение простейших показательных неравенств 4. Что нужно учесть при решении показательных неравенств? 5. Решение неравенств
Cлайд 3
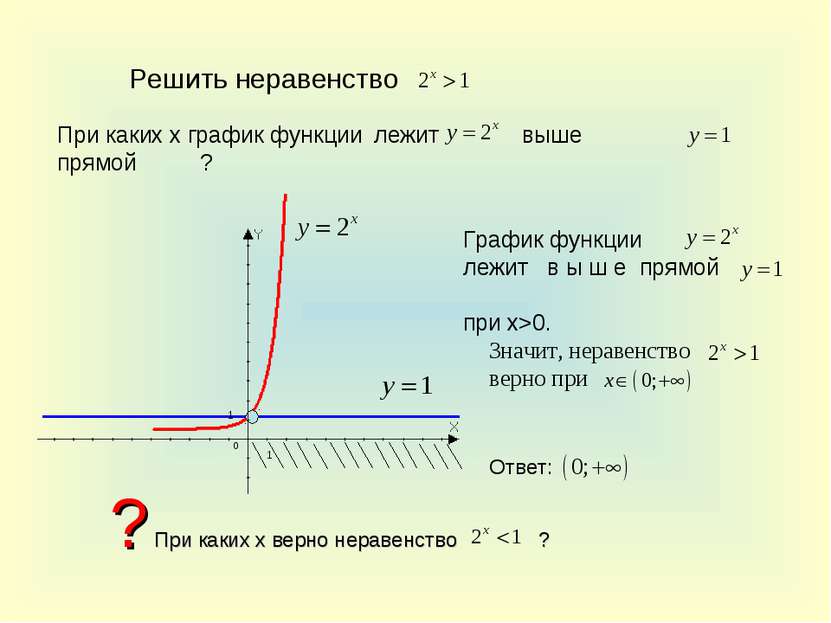
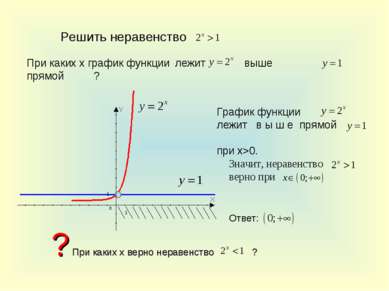Решить неравенство При каких х график функции лежит прямой ? выше График функции лежит в ы ш е прямой при x>0. Значит, неравенство верно при Ответ: ? При каких х верно неравенство ?
Cлайд 4
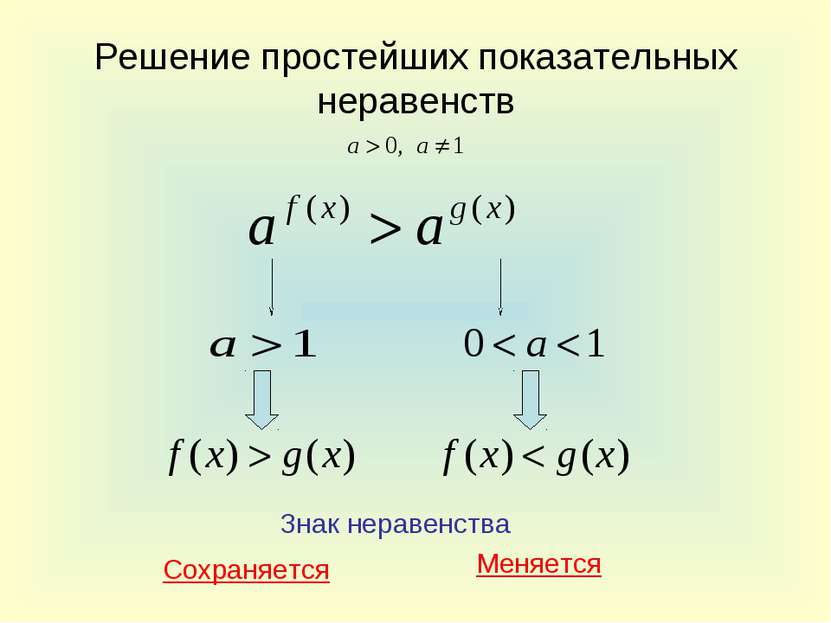
Простейшие показательные неравенства Определение: Неравенство, содержащее неизвестную в показателе степени, называется показательным неравенством. Определение: Неравенство в и д а называется простейшим показательным неравенством.
Cлайд 5
Решение простейших показательных неравенств Знак неравенства Сохраняется Меняется
Cлайд 6
Что нужно учесть при решении показательных неравенств ? Решить неравенство ? Что нужно учесть при решении простейших показательных неравенств ? 1. Привести основания степени к одинаковому основанию 2. Использовать свойства монотонной функции
Cлайд 7
Решите неравенства R Х-любое
Cлайд 8
Решите неравенство -5
Cлайд 9
Решите неравенство
Cлайд 10
Решите неравенство
Cлайд 11
Cлайд 12
Подведём итог Сегодня на уроке Я…
