X
Код презентации скопируйте его
Исследование функции на монотонность и экстремумы
Скачать эту презентацию
Презентация на тему Исследование функции на монотонность и экстремумы
Скачать эту презентациюCлайд 1
Материал к уроку по алгебре и началам анализа в 11 классе на тему: «исследование функции на монотонность и экстремумы » учитель Белова Н.И. МОУ «Храбровская СОШ»
Cлайд 2
Тема « Исследование функции на монотонность и экстремумы »
Cлайд 3
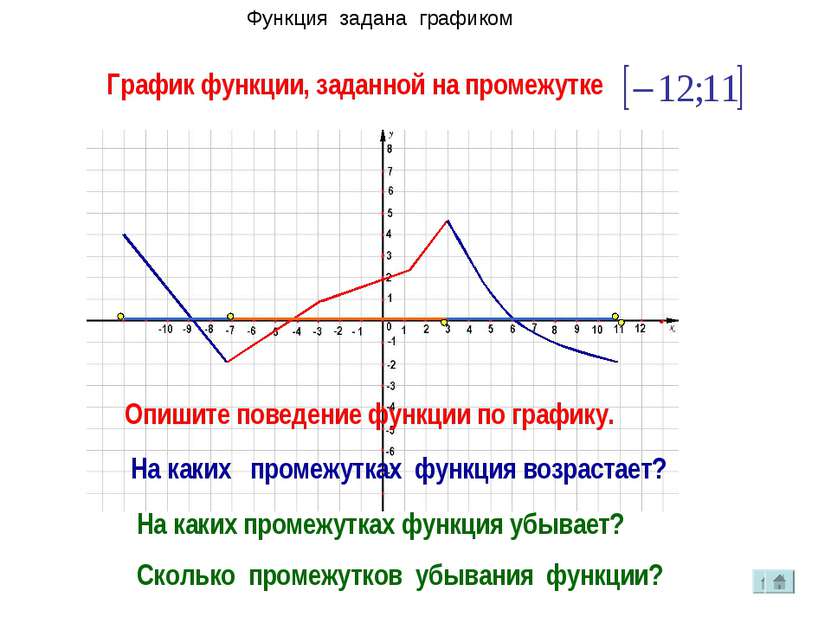
В экзаменационной работе по ЕГЭ часто встречаются вопросы: Назвать количество промежутков возрастания (убывания) функции. Указать наибольшую длину промежутка возрастания функции. Указать количество точек максимума или минимума и так далее.
Cлайд 4
Цели урока: 1.Обобщить и систематизировать материал по данной теме. 2.Продолжать развивать: наблюдать, рассуждать, анализировать, делать выводы. 3. Провести диагностику усвоения системы знаний и ее применения для выполнения практических заданий стандартного уровня / самостоятельная работа по тестам ЕГЭ /.
Cлайд 5
Монотонность функций
Cлайд 6
Вспомним определение возрастающей функции.
Cлайд 7
Рассмотрим график возрастающей функции
Cлайд 8
Вспомним определение убывающей функции Рассмотрим график убывающей функции
Cлайд 9
Рассмотрим график убывающей функции
Cлайд 10
Функция задана графиком
Cлайд 11
Cлайд 12
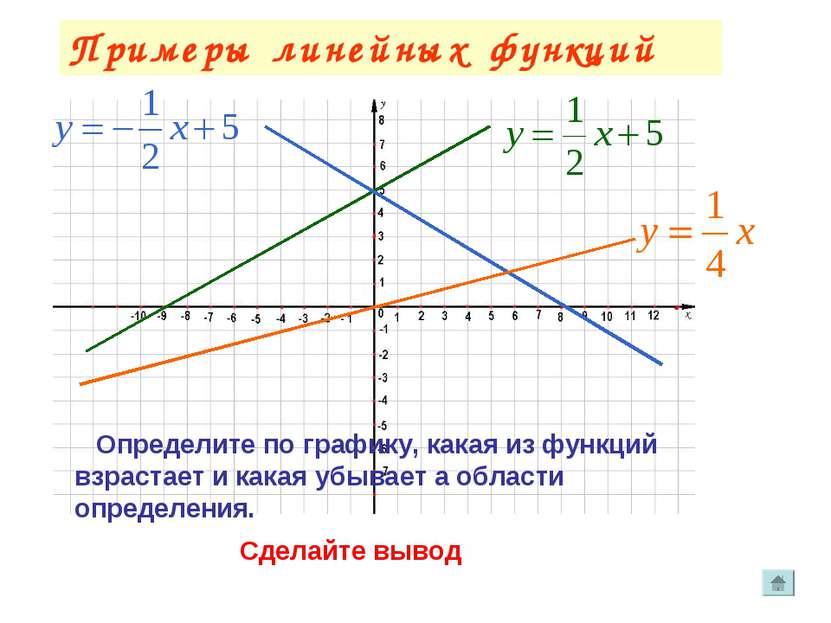
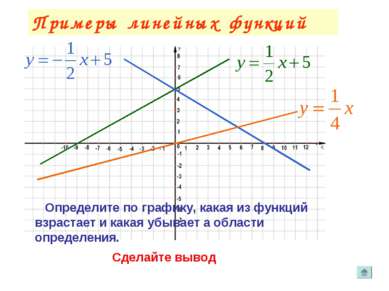
Функция задана формулой. Посмотрим – какая будет монотонность функции, и как можно это определить.
Cлайд 13
Но всегда так легко можно определить промежутки монотонности функции? Тогда на помощь к нам приходит производная.
Cлайд 14
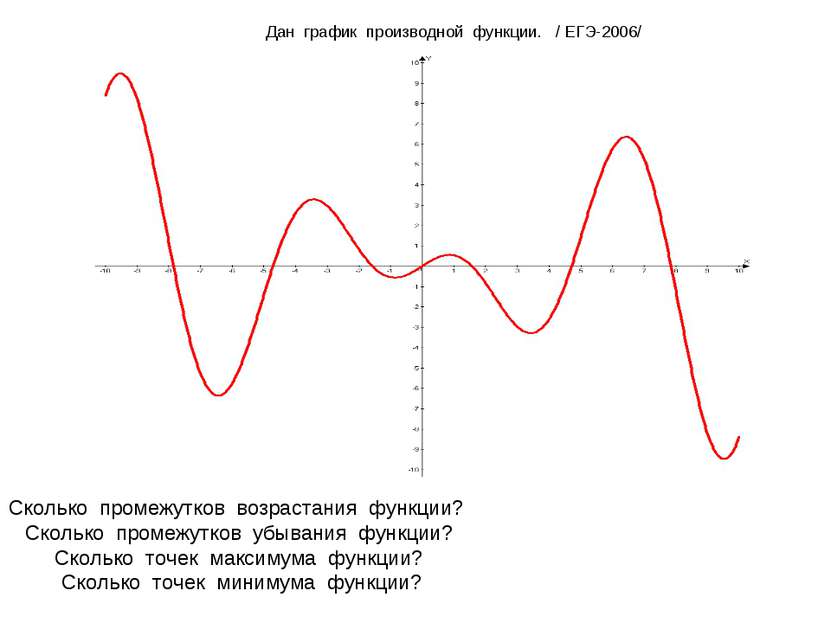
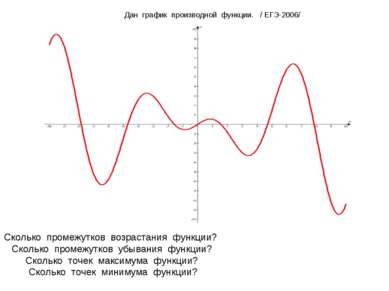Дан график производной функции. / ЕГЭ-2006/ Сколько промежутков возрастания функции? Сколько промежутков убывания функции? Сколько точек максимума функции? Сколько точек минимума функции?
Cлайд 15
Исследовать функцию на монотонность и на экстремумы. У(х)=х4 - 2х2+ 12
Cлайд 16
Подведем итог нашей работы
Cлайд 17
Монотонность функций Можно определить: по графику по производной
Cлайд 18
Самостоятельная работа. Работа с тестами. Предлагается два вида тестов, дифференцированных на два уровня изучаемой темы. А – минимальный уровень В – базовый уровень
Cлайд 19
Cлайд 20
Домашнее задание. № 956(1,3) № 957(1,3) № 958(1,3) № 959(1)
Cлайд 21
спасибо за внимание!
Cлайд 22
Молодцы!
