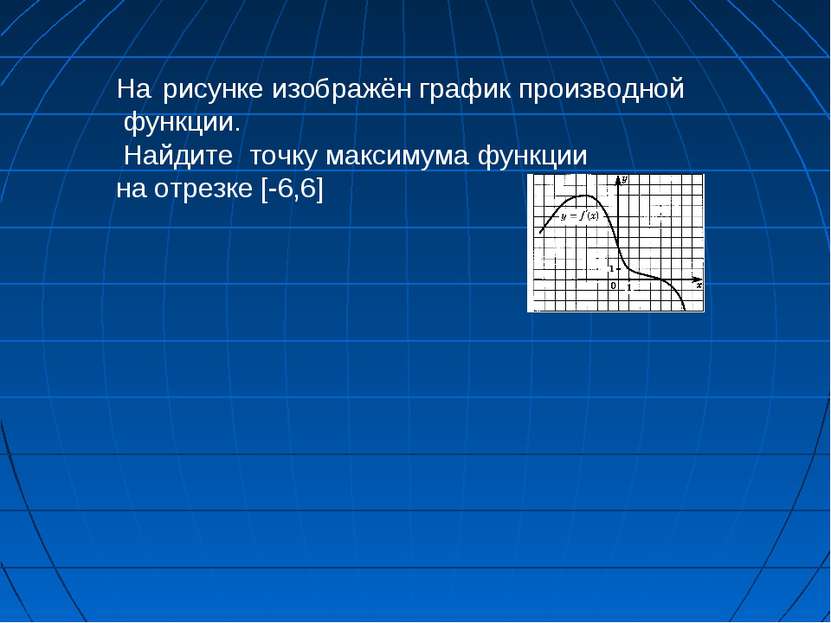
X
Код презентации скопируйте его
Применение производной к исследованию функции
Скачать эту презентацию
![Функция определена на отрезке [-4;4] . На рисунке изображён её график. Найдит...](https://bigslide.ru/images/19/18658/831/img6.jpg "Функция определена на отрезке [-4;4] . На рисунке изображён её график. Найдит...")
Презентация на тему Применение производной к исследованию функции
Скачать эту презентациюCлайд 1
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ возрастание и убывание функции МОУ Мешковская сош Учитель математики Ковалева т.в.
Cлайд 2
Цели урока: выяснение степени усвоения . правил вычисления производных; дать понятие «промежутка монотонности функции» уметь применять производную к нахождению промежутков возрастания и убывания функции; воспитание интереса к математике.
Cлайд 3
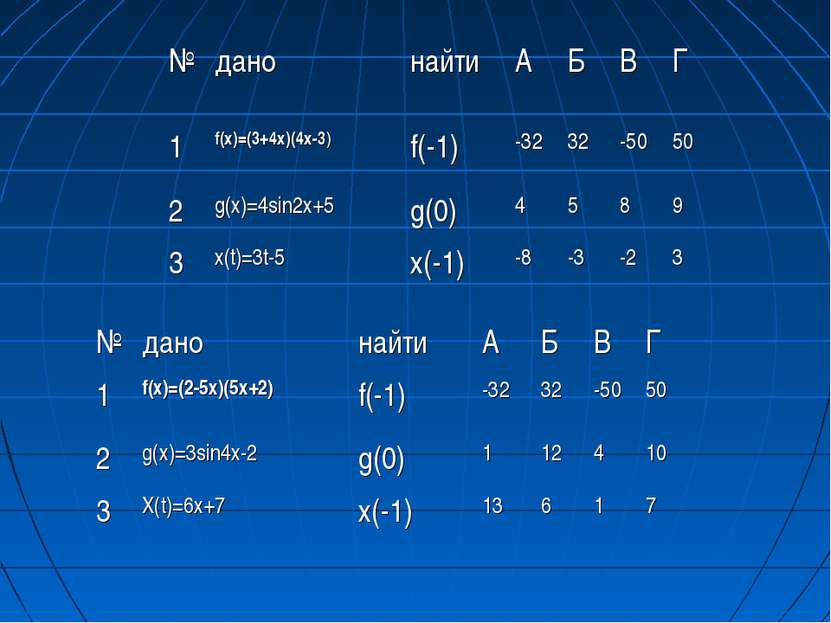
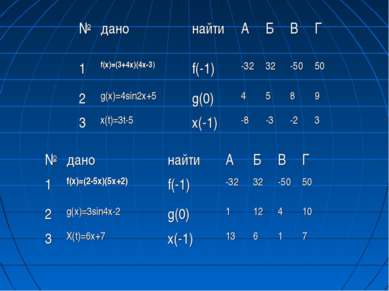№ дано найти А Б В Г 1 f(х)=(3+4х)(4х-3) f(-1) -32 32 -50 50 2 g(х)=4sin2х+5 g(0) 4 5 8 9 3 х(t)=3t-5 х(-1) -8 -3 -2 3 № дано найти А Б В Г 1 f(х)=(2-5х)(5х+2) f(-1) -32 32 -50 50 2 g(х)=3sin4х-2 g(0) 1 12 4 10 3 Х(t)=6х+7 х(-1) 13 6 1 7
Cлайд 4
Ответы: Вариант 1 А В Г Вариант2 Г Б Б
Cлайд 5
ЗАДАЧА Помните рассказ о бароне Мюнхгаузене? Пушка стреляет под углом к горизонту. На ядре сидит барон Мюнхгаузер. Определите характер движения ядра, еслиV0у=15м/с. g=10м/cc.,у0=0 Постройте графики движения и скорости
Cлайд 6
Производная- это скорость изменения функции она определяет поведение функции ВОПРОС. Как связаны производная и функция?
Cлайд 7
![Функция определена на отрезке [-4;4] . На рисунке изображён её график. Найдит...](https://bigslide.ru/images/19/18658/960/img6.jpg "Функция определена на отрезке [-4;4] . На рисунке изображён её график. Найдит...")
Функция определена на отрезке [-4;4] . На рисунке изображён её график. Найдите точку минимума этой функции на интервале (-3;3) Решение:
Cлайд 8
На рисунке изображён график производной функции. Найдите точку максимума функции на отрезке [-6,6]
Cлайд 9
ВОПРОС: Как найти интервалы возрастания и убывания функции?
Cлайд 10
Работа в классе Стр98-101 №1(1) №2(3) №2(1) самостоятельно
Cлайд 11
Основное применение производной- исследование функции с помощью производной и построение графика функции . Вопрос: Что вызывало затруднение? А что было интересно?
